基于非负矩阵分解的机场噪声监测点优化布局

李永华，唐先超

（1.中国民航大学 计算机科学与技术学院，天津300300；2.天津大学 计算机科学与技术学院，天津300072）

基于非负矩阵分解的机场噪声监测点优化布局

李永华1，唐先超2

（1.中国民航大学 计算机科学与技术学院，天津300300；2.天津大学 计算机科学与技术学院，天津300072）

近年来国内民航迅速发展，机场的新建、扩建和航空运输量的持续增长使得机场噪声污染事件不仅持续上升，而且噪声污染程度也日益加重，因而强化机场附近噪声污染的监测对机场建设及其环境评估十分重要。针对机场噪声污染监测问题，提出一种基于非负矩阵分解(NMF)方法对机场噪声监测点布局问题进行优化求解。该方法以大量网格点作为候选监测点，对单个飞机噪声事件候选监测点的噪声值所形成的矩阵按非负矩阵分解进行区域划分,得到噪声影响子区域。进一步以各子区域的中心点作为该区域的噪声影响代表点,以此确定机场噪声监测点数目和位置。研究结果表明所获得的解比贪心算法得到的解更优，需要的监测点更少。

声学；机场噪声；非负矩阵分解；监测点布局；区域划分

近年来，由于国内民航发展迅速，新建、扩建机场和持续增长的航空运输量使得机场噪声问题愈发严重，噪声环境污染程度日益恶化，噪声环境影响投诉也逐年增多，机场经营者日趋被动、机场噪声问题正在成为影响民航业可持续发展的障碍之一。

机场噪声监测和预测是机场噪声环境影响评估的基本前提，而机场环境影响评估是机场噪声控制、机场规划设计及城市规划的重要依据。目前，机场噪声监控系统在发达国家，特别是位于城市敏感目标密集处的机场（包括我国首都机场、香港、台湾等地区机场）已普遍应用，世界上前100个最繁忙机场中约85%建立了噪声监测与管理系统[1]。

现阶段，我国机场噪声自动监测系统均由国外研制，成本高且噪声计算模型、噪声评价指标、软硬件设计都没有具体考虑国内机场的运行特征，导致实际应用过程中难以充分发挥效用，系统的核心技术受制于人。更为重要的是，目前的机场噪声监测系统，由于缺少理论方法和技术的支持，其监测点布局主要借助专家经验完成，受监测模式、成本等局限，监测点数量较少，无法实现机场周围噪声的全面精确度量。

监测点布局优化理论和模型的研究有利于实现低成本条件下对噪声分布的有效监控，包括相关分析和聚类分析等统计学方法，以及多目标优化等数学方法已经应用在许多其他工程领域。例如，针对无线传感器网络的布点优化，Maytham Safar等人研究了无线传感器网络的顶点覆盖模型；针对河流系统的水质监测，Ilker T.Telci等人设计了顶点覆盖模型来优化；李静等人利用最小顶点覆盖改进了基于时间满意的应急物资储备库选址模型等。在机场噪声监控布点优化方面，丁文婷等人[2]通过建立最小顶点覆盖模型，计算了单个飞机噪声事件条件下，机场噪声监测优化布点方案，但是整体上有关机场噪声监控布点优化布局的应用研究报道较少。

本文通过应用美国联邦航空条例第150部（FAR Part 150）规定使用统一的综合噪声模型INM（Integrated Noise Model）进行机场噪声预测计算[3,4]。在应用INM获得中小型机场噪声分布数据的基础上，考虑单个飞机噪声事件（即飞机飞行一次产生的噪声，特别是指高噪声）对机场周围居民的影响，通过对单个飞机噪声事件噪声值所形成的矩阵进行非负矩阵分解，得到噪声影响子区域及其代表点，从而为机场噪声监测布局优化提供理论依据。

1 机场噪声网格划分

将机场周围噪声影响区域划分为若干个网格，参考INM[5]标准网格大小设置为120×120，如图1所示。记录各网格点的多次飞行事件的噪声值，形成各顶点多个噪声事件的噪声值矩阵Val_Noise。矩阵中一行表示某个顶点的50次噪声事件的噪声值，一列表示一次飞行事件的噪声值。

图1 机场周围区域网格划分示意图

2 基于灰色理论的关联度

非负矩阵分解对社区进行划分考虑的最重要部分是关联矩阵的获取。本文中关联矩阵考虑的是各个网格点之间的关联程度。文中划分的网格为120×120，即网格点数为14 400个，因此关联矩阵的大小为14 400×14 400。网格点之间的关联程度有很多算法，余弦相似度、欧式距离、灰色关联度等[6,7]。灰色距离[8,9]考虑的是比较序列和参考序列之间的差异信息，它以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控。鉴于噪声序列考虑的是有限次数的噪声事件，因此关联矩阵考虑的是灰色距离。

设Xi为系统因素，其在序号k上的观测数据为Di，k=1,2,…,n，则称

为因素Xi的行为序列。

设Xi=(xi(1),xi(2),...,xi(n))为因素Xi的行为序列，Di为序列算子，且

其中

则称Di为均值化算子，XiDi为Xi在均值化算子Di下的像，简称均值像。

设系统行为序列

对于ξ∈(0,1)，令

其中ξ称为分辨系数，通常取0.5，则γ() X0,Xi为因素X0和因素Xi之间的灰色关联度。

按照上述方式计算各个点之间的关联度，得到如下的关联度矩阵Val_Gray(gij)(i，j∈{1,2,3,...,n})。

3 非负矩阵分解

非 负 矩 阵 分 解(Non-negativeMatrix Factorization，NMF)[10]是1999年由Lee和Seung提出的，由于其分解后的矩阵所有元素非负，纯加性的描述符合人们整体是由部分组成的直观感知。非负矩阵分解自从被提出以来，被广泛应用于诸多领域，如图像处理、文本聚类、语音识别以及生物和化学等领域。

传统的NMF问题可描述如下：给定m×n元素非负的矩阵V，通过求解算法得到m×k的矩阵W和k×n非负矩阵H使得：V≈WH，k满足(m+n)k≪mn。NMF是一个非凸的不等式约束优化问题，其数学表现形式如下

其中W为基矩阵，H为编码矩阵。非负矩阵分解一般通过迭代的方式进行求解，迭代规则为[11]

通过对原始矩阵进行非负分解，得到m×k的基矩阵W，m表示节点的数目，k表示类别的数目，W中的元数wij表示第i个点属于第j个类别的概率。文中采用最大概率隶属原则，即隶属于第i行最大的wij对应列的类别(类别j)。对每个点进行划分，得到所有点的类别结构。

4 实验

4.1 噪声监测数据的获取

实验模拟了某中小型机场的120×120的网格区域的50个航班计划，每次航班由不同的飞行机型、飞行坡面、飞行航迹构成[2]。获取各个模拟监测点的噪声数据，得到14 400×50的一个噪声值矩阵(Val_Noise)如下。

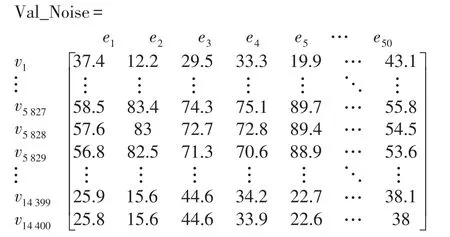
Val_Noise中的每列表示单次飞行对120×120网格产生的一次噪声数据，每行表示该行号对应顶点的50次飞行的噪声数据。Val_Noise() ij表示第i个顶点在第j次飞行事件中的噪声值。图2为120×120的网格的一次噪声事件的监测值。

图2 120×120的网格的一次噪声事件的监测值

4.2 基于NMF的噪声事件最小顶点覆盖模型

对关联矩阵进行NMF分解，得到如下的W∗。W∗中省略部分的值接近0，分解的非零列对应最终划分的类别数，各行对应的最大值所在的列即为该行对应的顶点所属的类别。

按照最大隶属度原则，得到如图2所示的5个中心点，纵坐标为中心点在50次噪声事件中的噪声值，其对应的位置为矩阵中的69、260、411、443、628列。

图3中每个类别包含的点数分别如表1所示。

图3 69、260、411、443、628列50次噪声事件中的噪声值

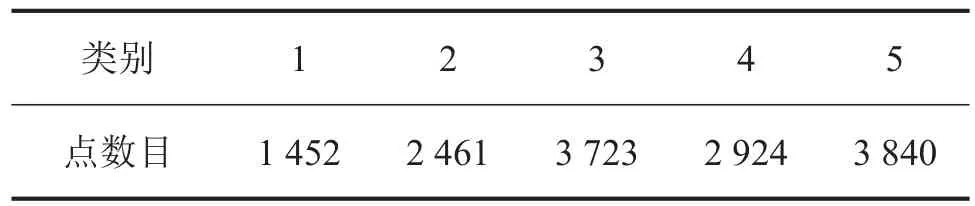
表1 类别包含点数统计表

对各类别中的点用不同的颜色进行绘制，得到区域划分的结果如图4(a)所示。在各区域中顶点之间的关联程度较高，区域之间的联系较为稀疏。图中区域1内噪声值最高，区域5噪声值最低。把各区域内的中心点作为该区域的噪声监测点得到图4(b)的5个噪声监测点，利用这5个监测点可以监测该区域的噪声变化情况，依据各个顶点之间的关联关系，可以得到其它顶点的噪声值。

图4 噪声影响区域的划分及监测点布局

图5为贪心算法所得检测点布局结果。通过对比图5和图4所得结果可以看出，一方面NMF方法所需要的噪声监测点覆盖范围较大，同时检测点分布更为均匀；另一方面在达到同等检测效果的前提下，NMF方法比贪心算法得到的6个监测点数[2]更少。因此可以认为，NMF方法可以相对更好的监测机场周边所有区域，实现监测优化的目的。

5 结语

本文利用中小型机场单次航班对机场附近地区噪声污染的数据，提出了基于NMF进行噪声区域划分，从而获得单个飞机噪声事件最小顶点覆盖模型的监测点分布方法。实验表明基于NMF方法以及顶点之间的关联，需要的监测点更少。在这些类别中心顶点设立监测点，能用最少的监测点监测到所有的飞机噪声事件。

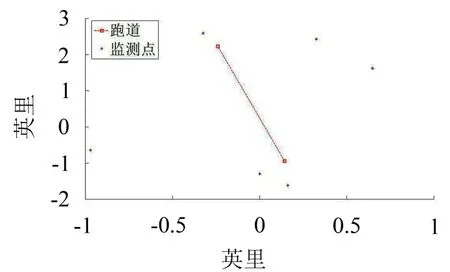
图5 贪心算法监测点布局

[1]上海市环境科学研究院.虹桥国际机场航空器噪声监控系统项目建议书暨工程可行性研究报告[R].2010.

[2]丁文婷，徐涛，杨国庆.单个飞机噪声事件最小顶点覆盖模型的几场噪声监测点分布方法[J].噪声与振动控制，2012，32(3).

[3]Forsyth D W,Gulding J,Dipardo J.Review of Integrated noise model(INM)equations and processes[R].NASA CR-2003-212414,May,2003.

[4]Faa.FAR 150,Airport noise compatibility planning[M].USA,2006.

[5]Dipardo D W F J.Review of integrated noise model(INM) equations and processes[R].2003.

[6]张庆友，许禄.DNA编码序列的图形表示及相似度计算[J].高等学校化学学报，2002(7).

[7]范常忠，周喜.灰色系统理论在城市区域噪声研究中的应用[J].噪声与振动控制，1997(5)：24-26.

[8]易德生，郭萍.灰色理论与方法：提要·题解·程序·应用[M].石油工业出版社，1992.

[9]邓聚龙，郭洪.灰色理论[M].武汉：华中科技大学出版社，2002.

[10]Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401 (6755)∶788-791.

[11]Seung D,Lee L.Algorithms for non-negative matrix factorization[J].AdvancesInNeuralInformation Processing Systems,2001,13∶556-562.

Optimal Locating Method for the Layout ofAirport Noise Monitoring Sites Based on Non-negative Matrix Factorization

LI Yong-hua1,TANG Xian-chao2

(1.College of Computer Science and Technology,CivilAviation University of China, Tianjin 300300,China; 2.School of Computer Science and Technology,Tianjin University,Tianjin 300072,China)

∶With the rapid development of domestic civil aviation in recent years,noise pollution of airports is becoming a serious problem.Thus,strengthening the noise monitoring in the airport vicinity is very important for airport construction and environmental evaluation.Aiming at the monitoring of airport noise pollution,an optimization method based on nonnegative matrix factorization(NMF)is put forward to optimize the layout of the noise monitoring sites.In this method,large number of the grid nodes is employed as the candidate monitoring points,and the non-negative matrix composed of the noise values from single flight event at the candidate monitoring points is formed.Then,the non-negative matrix is factorized to obtain the effective subdivision of noise.Furthermore,the location and number of the noise monitoring sites are determined by the representative central point of the effective subdivisions.It is shown that this method needs fewer monitoring locating sites and can get better results than the greedy algorithm.

∶acoustics;airport noise;NMF;location of monitoring sites;region division

X839< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.026

1006-1355(2014)06-0117-04+130

2014-03-27

李永华（1974-），女，内蒙古赤峰市人，讲师，主要从事软件测试工作。

E-mail∶yh-li@cauc.edu.cn