基于FLAC-3D强度折减法的边坡稳定性影响因素敏感性分析

梅 岭, 季佩祥, 张太玥

(江苏科技大学 土木工程与建筑学院,江苏 镇江 212003)

基于FLAC-3D强度折减法的边坡稳定性影响因素敏感性分析

梅 岭, 季佩祥, 张太玥

(江苏科技大学 土木工程与建筑学院,江苏 镇江 212003)

通过建立均质土坡模型,利用FLAC-3D 软件的强度折减法,求解边坡稳定系数,系统地研究了边坡稳定性影响因素的敏感性问题.利用边坡稳定安全系数以及塑性贯通区作为边坡失稳的判据,通过每次改变一个参数变量来确定稳定系数Fs与岩体力学参数的关系,找出敏感性最强的因素,结果表明:内摩擦角敏感性最强,粘聚力和土体重度次之,但两者之间没有定量的关系.

FLAC-3D; 边坡稳定; 敏感性分析

工程实践表明,滑坡严重威胁我国国民的生产和生活安全,其稳定性已成为我国目前工程建设中亟待解决的问题之一.影响滑坡稳定性的主要因素有滑带土的组构特性、物理力学特性以及滑带土的强度特性.因此,合理确定滑带土的力学参数是判断滑带稳定与治理的关键[1].由于岩土体具有随机性、模糊性及可变性等特点,在实际勘察设计中主要针对影响边坡稳定的较敏感的参数作敏感性分析[2].基于此,文中利用FLAC-3D软件对边坡稳定的主要影响因素,如粘聚力、内摩察角以及土体的重度分别作敏感性分析.

1 FLAC-3D强度折减法原理

强度折减法中边坡的安全系数定义为使边坡刚好达到临界破坏状态时,对其强度参数进行折减的程度,即岩土体的实际抗剪强度与临界破坏时的折减后剪切强度的比值.若边坡采用Mohr-Coulomb准则,影响其稳定性的强度参数是粘聚力c和内摩擦角φ,将坡体原始的粘聚力c0和内摩擦角φ0同时除以一个折减系数Ks,然后进行数值分析[3].通过不断增大Ks,反复分析直至边坡达到临界破坏状态,此时的折减系数即为安全系数Fs.假设此时粘聚力和内摩擦角为ccr和φcr,据此可得原始边坡对应的安全系数为:

(1)

2 三维边坡稳定性影响参数的敏感性分析

某边坡基本概况[4]如下:均质土坡,坡高10 m,坡脚为45°,坡脚到左侧边界的距离为2 m,坡顶到右侧边界的距离为8 m,坡脚向下延伸距离为3m.其基本的岩土体物理力学参数指标如表1所示,模型的具体尺寸见图1(y方向垂直于纸面,长度取4 m).

表1 物理、力学参数指标

Table 1 Index of physical,mechanical parameters on soil

密度ρ/kg·m-3体积模量K/MPa剪切模量G/MPa粘聚力c/kPa内摩擦角φ/(°)正应力σt/MPa20001003012.382010000

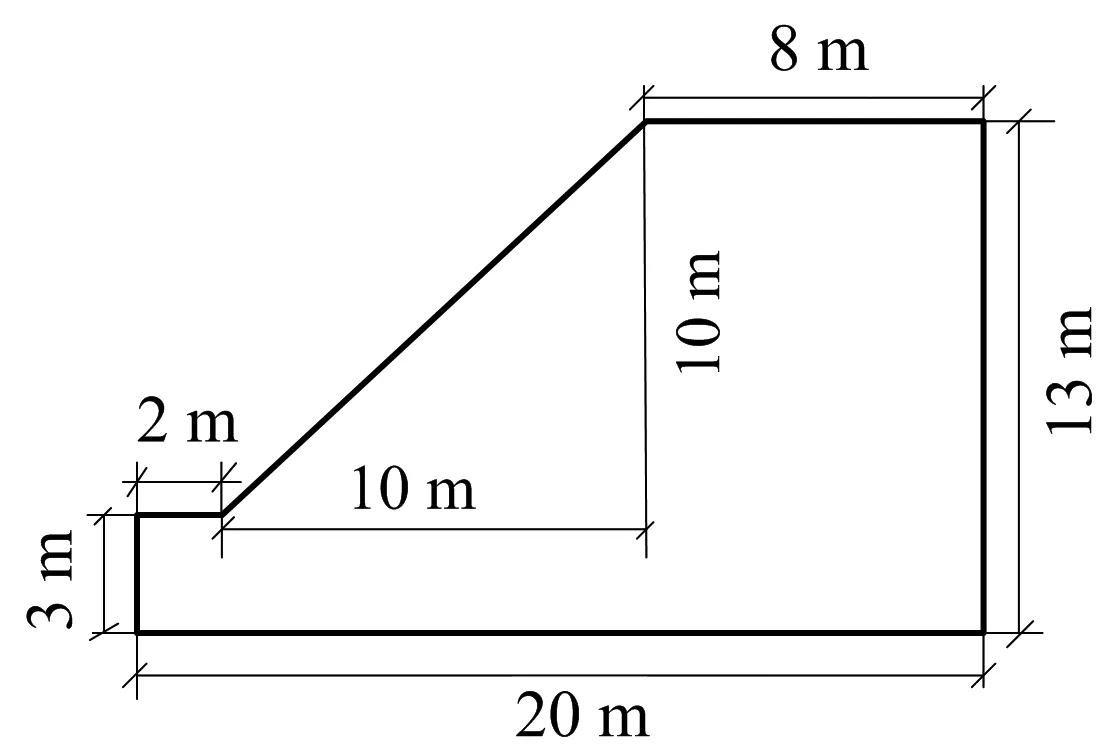
图1 边坡平面尺寸模型示意

为了反映边坡的实际状态,本模型还将边坡底部的x,y和z方向进行固定,并将边坡各边界的速度予以固定.所建模型采用的是Mohr-Coulomb准则,按自重应力的作用考虑模型的初始应力场,计算收敛的准则是确定模型内部各点的不平衡比率满足小于10-5的求解要求.经FLAC-3D计算分析后，最终所得的剪应变云图及塑性区的分布情况如图2所示.

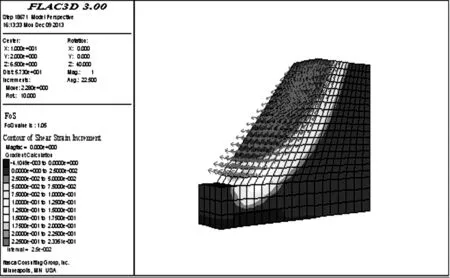
图2 算例模型剪切应变增量云图及速度矢量

从图中可以得到该算例模型的最终安全系数为1.05,其塑性贯通区域已经贯穿整个边坡,形成了潜在的滑动面,说明这一区域已经出现了明显的滑动,边坡此时发生了破坏.

由于数值模拟技术的发展,数值分析软件较传统的理论分析方法具有考虑因素全面、计算快捷等特点,基于此,可以通过FLAC-3D求解边坡稳定安全系数来分析不同参数间的敏感程度.由于FLAC-3D编程时需要设置的参数众多,故采取对边坡稳定性影响重大的主要参数进行敏感性分析.在阅读相关文献的基础上选取粘聚力c、内摩擦角φ以及土体重度γ作为主要研究对象来考察其对边坡稳定性的影响程度.使用FLAC-3D分析边坡的稳定性状态的基本步骤如上所述,具体的计算方法是每次只改变一个参数,而其他所需的参数则保持不变,最终建立的计算方案如表2所示.

表2 具体的计算方案

2.1c与φ关于Fs的敏感性比较分析

当γ=20 kN/m3时,分别通过改变c与φ的值来考察边坡的稳定安全系数,经FLAC-3D有限差分法计算后,分别得到粘聚力c固定时,φ与Fs的关系曲线以及φ固定时,c与Fs的关系曲线,结果分别如图3,4所示.

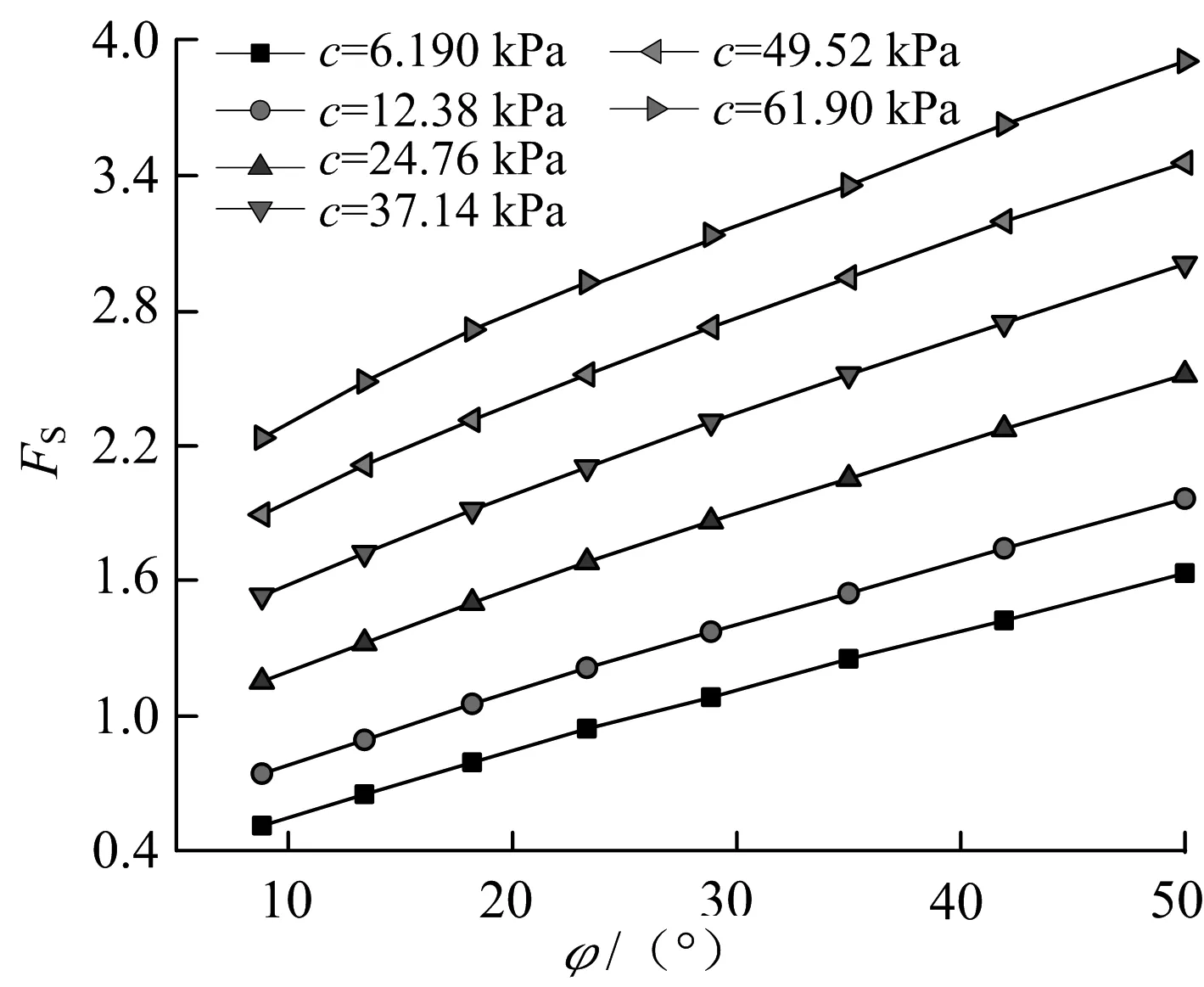
图3 φ与Fs的关系曲线

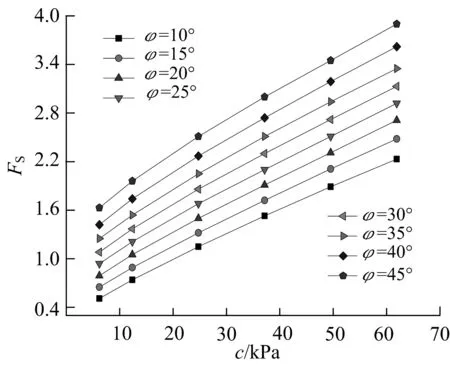
图4 c与Fs的关系曲线

从以上c、φ与Fs的关系曲线图中可以得出:无论粘聚力还是内摩擦角都与边坡的稳定安全系数近似成线性关系，且Fs分别随着c和φ的增大而增大.现分别取其中的一条曲线进行c与Fs和φ与Fs的曲线关系拟合,所得的结果分别如图5,6所示.

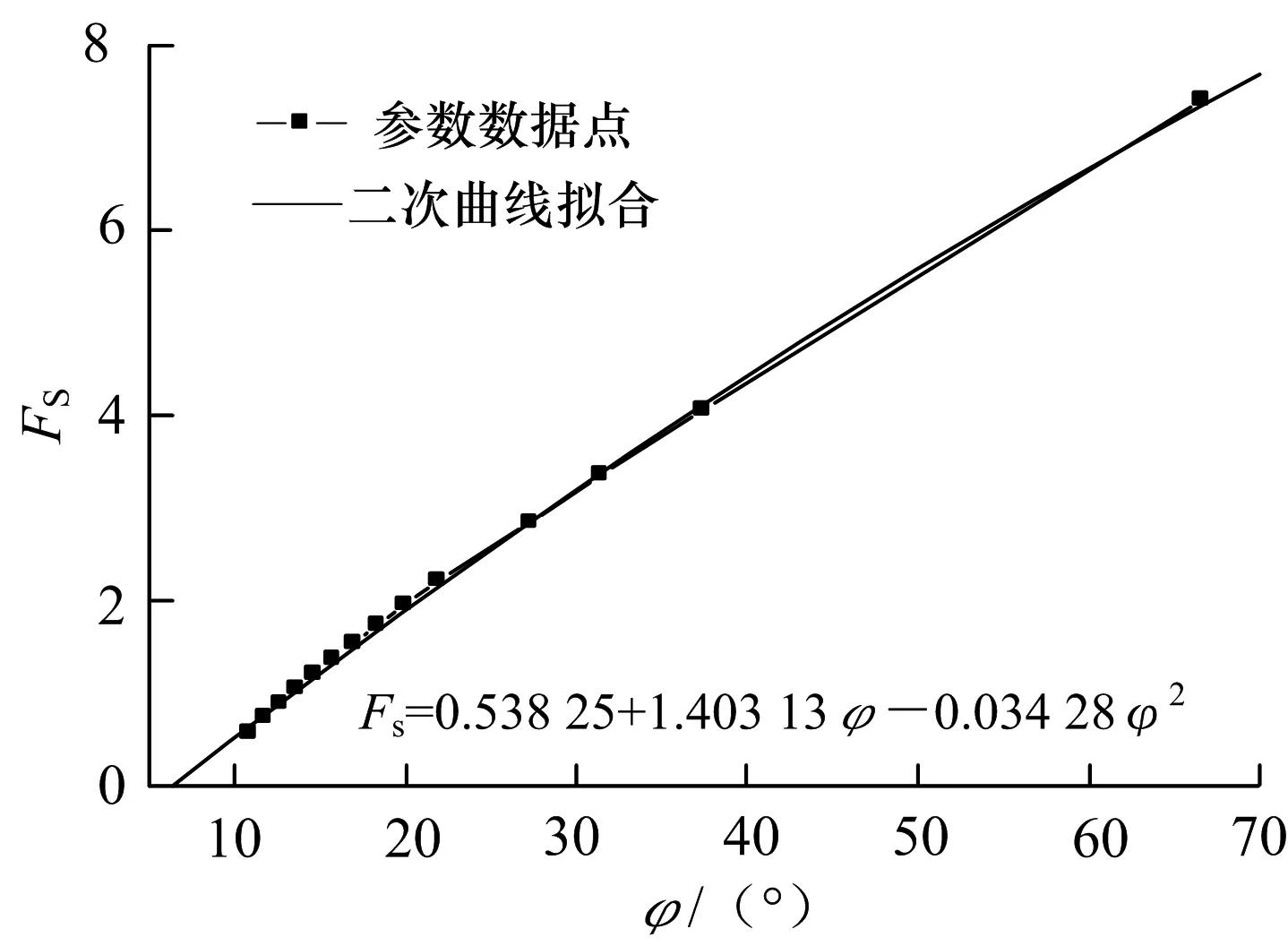
图5 φ与Fs的拟合关系曲线

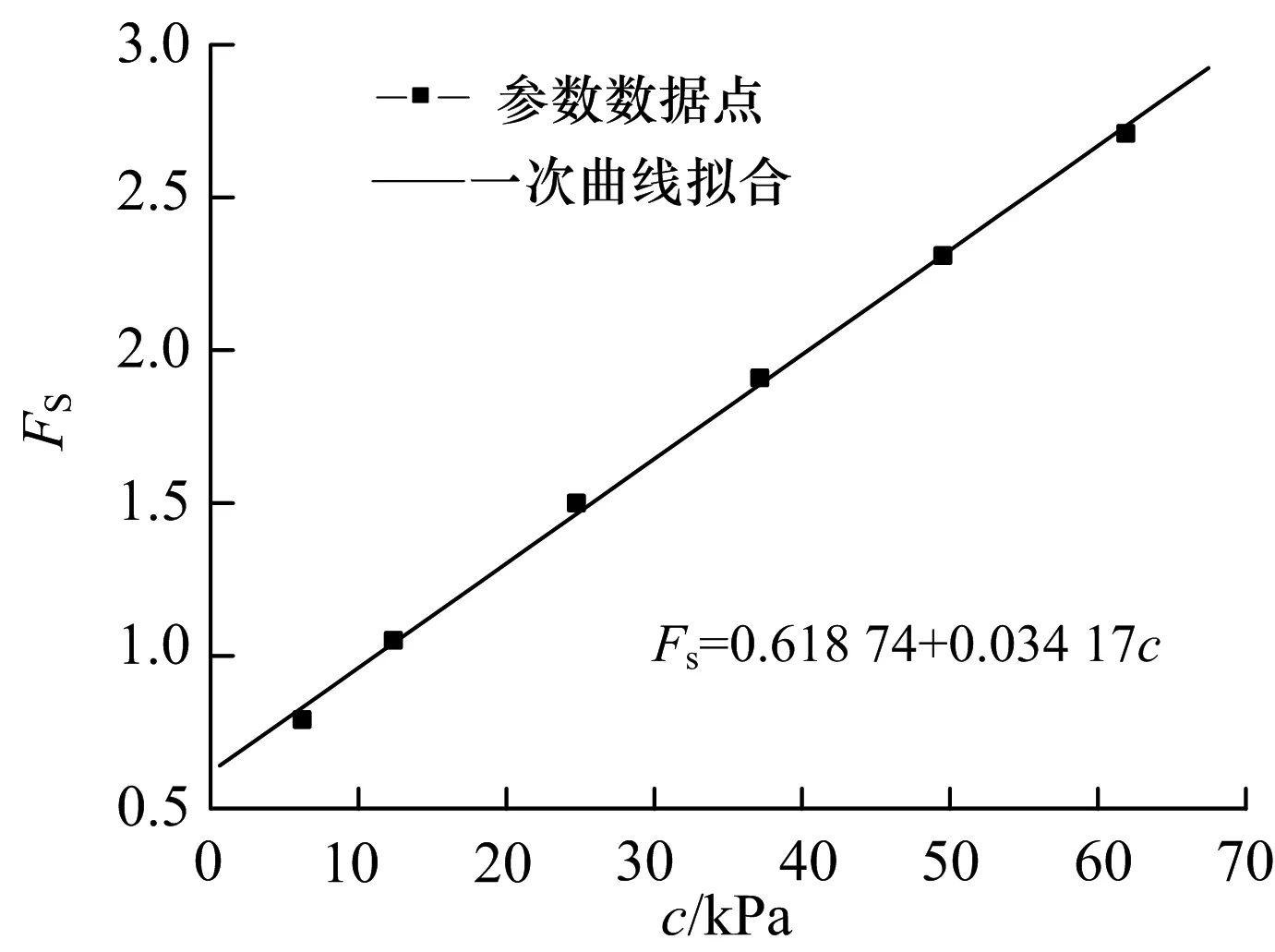
图6 c与Fs的拟合关系曲线

从c与Fs以及φ与Fs的拟合曲线关系图中可知,当γ=20 kN/m3时,图5，6中的相关系数分别为0.998 6和0.998 2,即以上曲线拟合的可信度非常高.由于Fs与φ拟合的曲线为二次抛物线,Fs与c拟合为一次线性函数,故可以通过二次函数的割线模量与一次函数的比例系数来判断各自的敏感性程度.因为图5中的割线模量为1.216 8远大于图6中的0.034 2,故可以最终判断φ对边坡稳定性的敏感程度高于c对边坡稳定性的敏感程度.

2.2γ与φ关于Fs的敏感性比较分析

当c=12.38 kPa时,分别通过改变γ与φ的值来考察边坡的稳定安全系数,经FLAC-3D有限差分法计算后,分别得到γ固定时,φ与Fs的关系曲线以及φ固定时,γ与Fs的关系曲线,结果分别见图7,8.

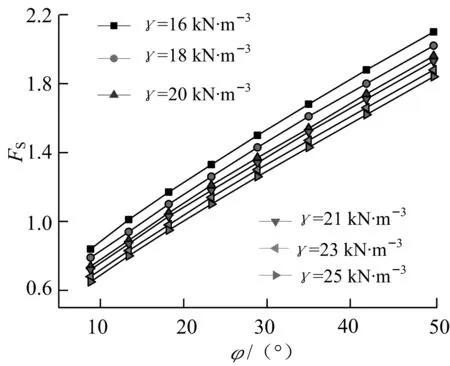
图7 φ与Fs的关系曲线

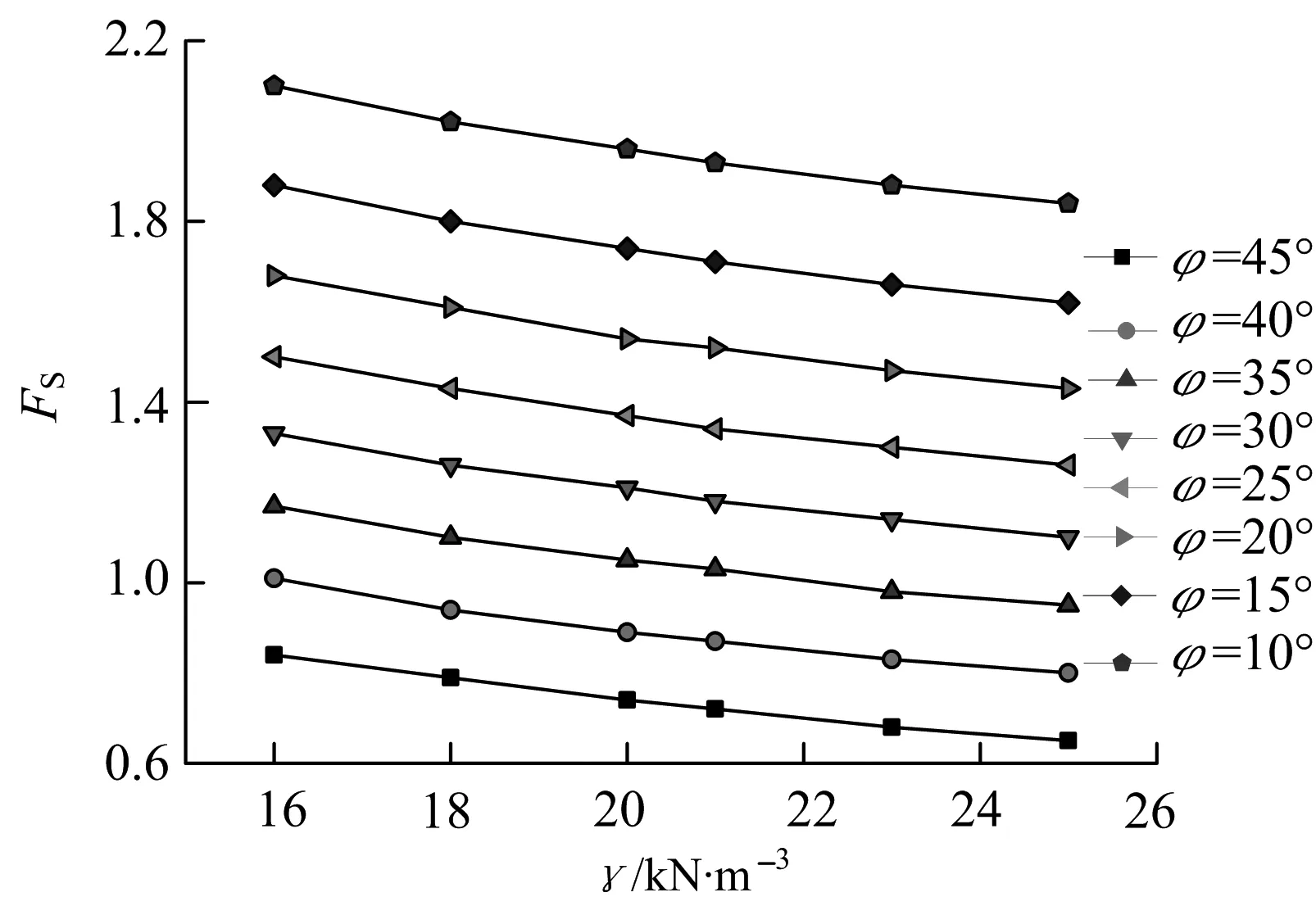
图8 γ与Fs的关系曲线

从以上γ，φ与Fs的关系曲线图中,可以得出,无论土体重度还是内摩擦角都与边坡的稳定安全系数近似成线性关系,但是Fs随着φ增大而增大,而Fs随着土体重度增大而减小.从图8中取一条曲线进行γ与Fs的关系曲线拟合,所得的结果如图9所示.

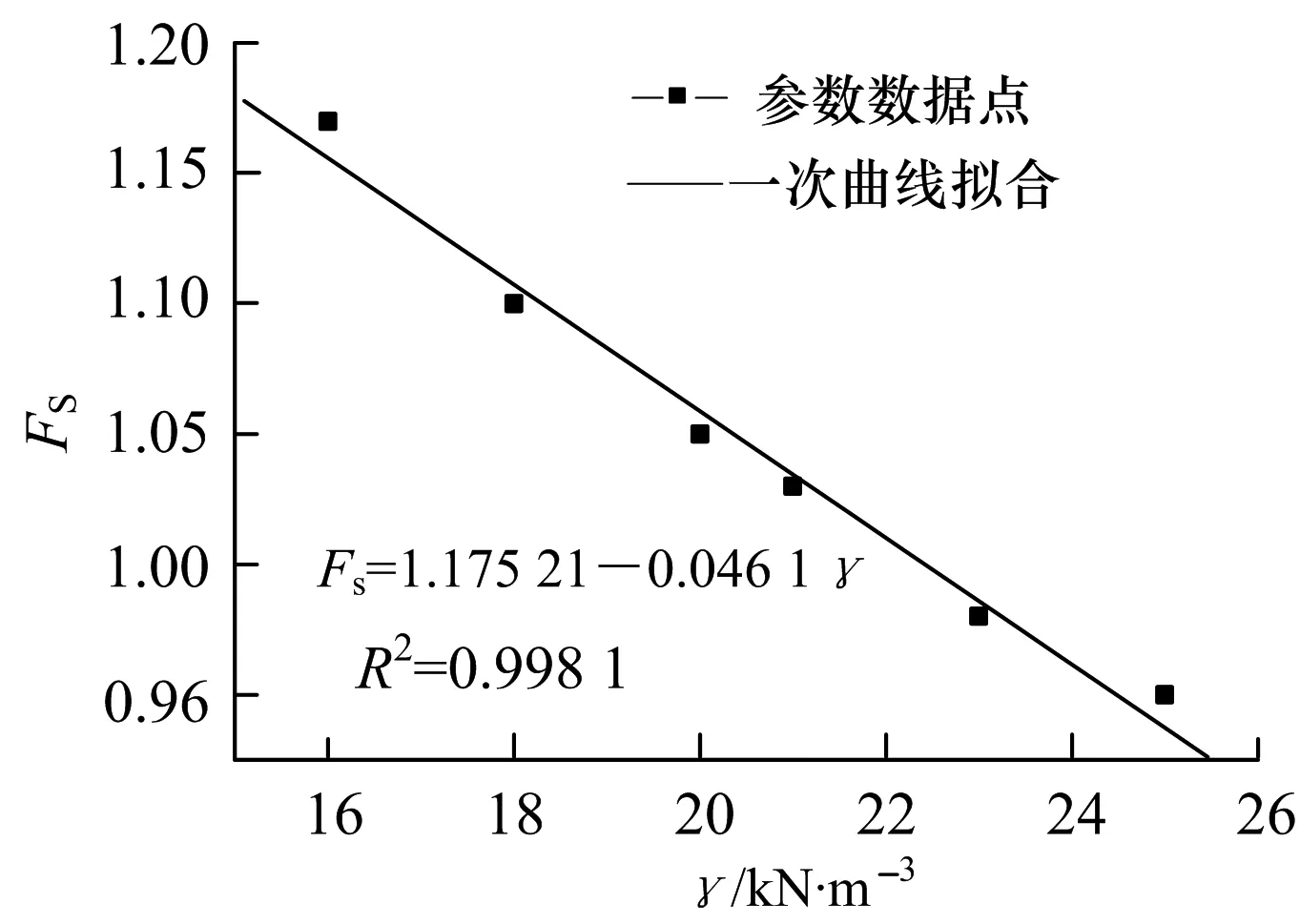
图9 γ与Fs的拟合关系曲线

由图9可以知道,γ与Fs则最终拟合为一次直线,其比例系数为0.024 3,远小于图5中的1.216 8,故可以最终判断φ对边坡稳定性的敏感程度高于γ对边坡稳定性的敏感程度.

2.3γ与c关于Fs的敏感性比较分析

当φ=20°时,分别通过改变c与γ的值来考察边坡的稳定安全系数.经FLAC-3D有限差分法计算后,分别得到γ固定时,c与Fs的关系曲线以及c固定时,γ与Fs的关系曲线,其结果分别如图10,11所示.

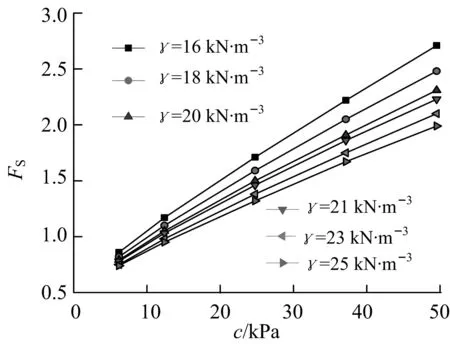
图10 c与Fs的关系曲线

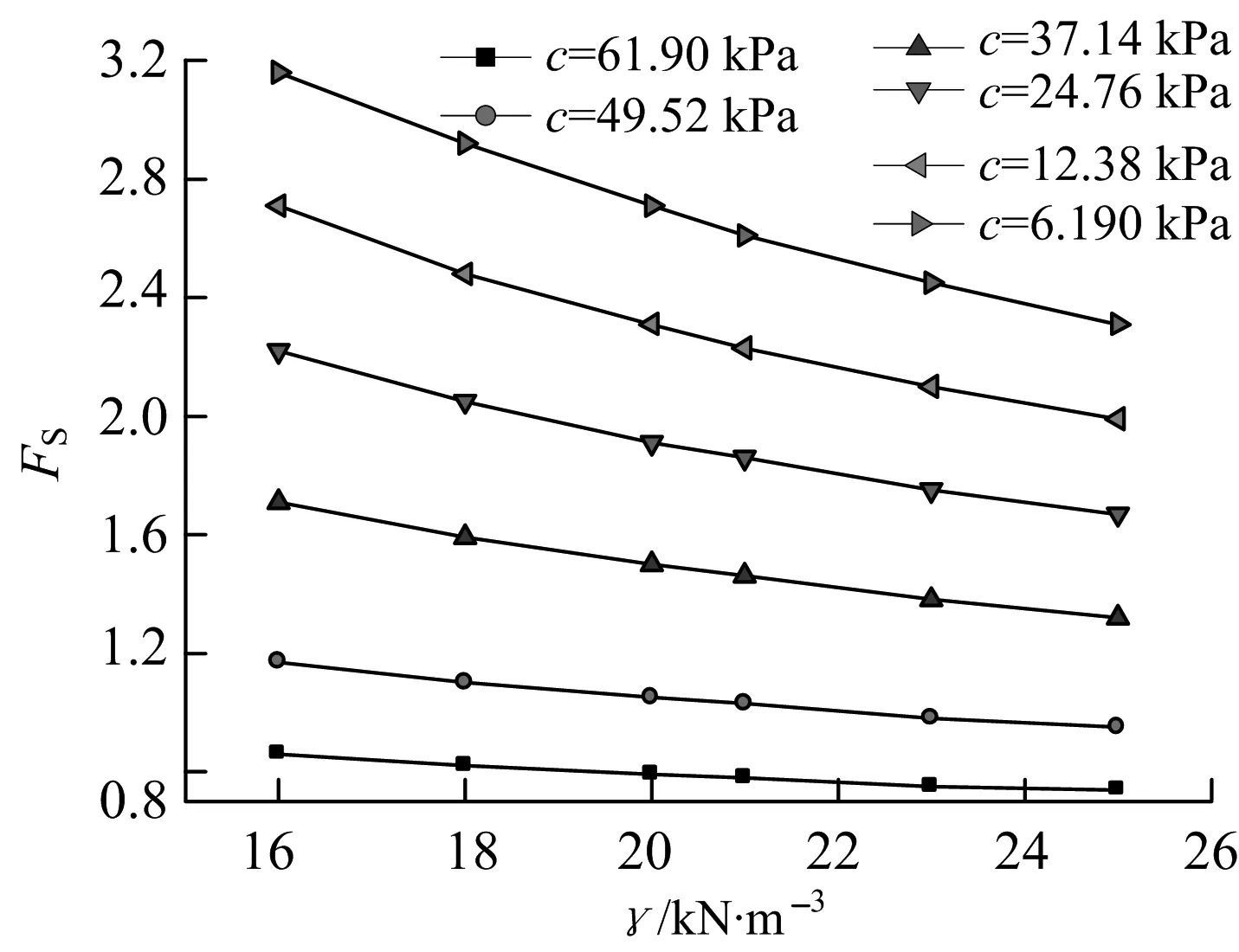
图11 γ与Fs的关系曲线

从以上γ、c与Fs的关系曲线图中,可以得出,无论土体重度还是粘聚力都与边坡的稳定安全系数近似成线性关系:随着粘聚力的增大,边坡越来越稳定,而随着土体重度的增大,边坡则逐渐有失稳的趋势.现从图11中取两条曲线进行γ与Fs的曲线关系拟合,所得的结果如图12所示.

由γ与Fs的拟合曲线关系图12可知,该图中一次线性拟合曲线的比例系数为0.024 3,小于图6中c与Fs的比例系数0.034 2,可以判断c对边坡稳定性的敏感程度高于γ对边坡稳定性的敏感程度;但是研究发现,当c=37.14 kPa时,γ与Fs的一次线性拟合曲线中的比例系数为0.060 8高于图6中的0.034 2,所以当c=37.14 kPa时γ对边坡稳定性的敏感程度高于c对边坡稳定性的敏感程度.

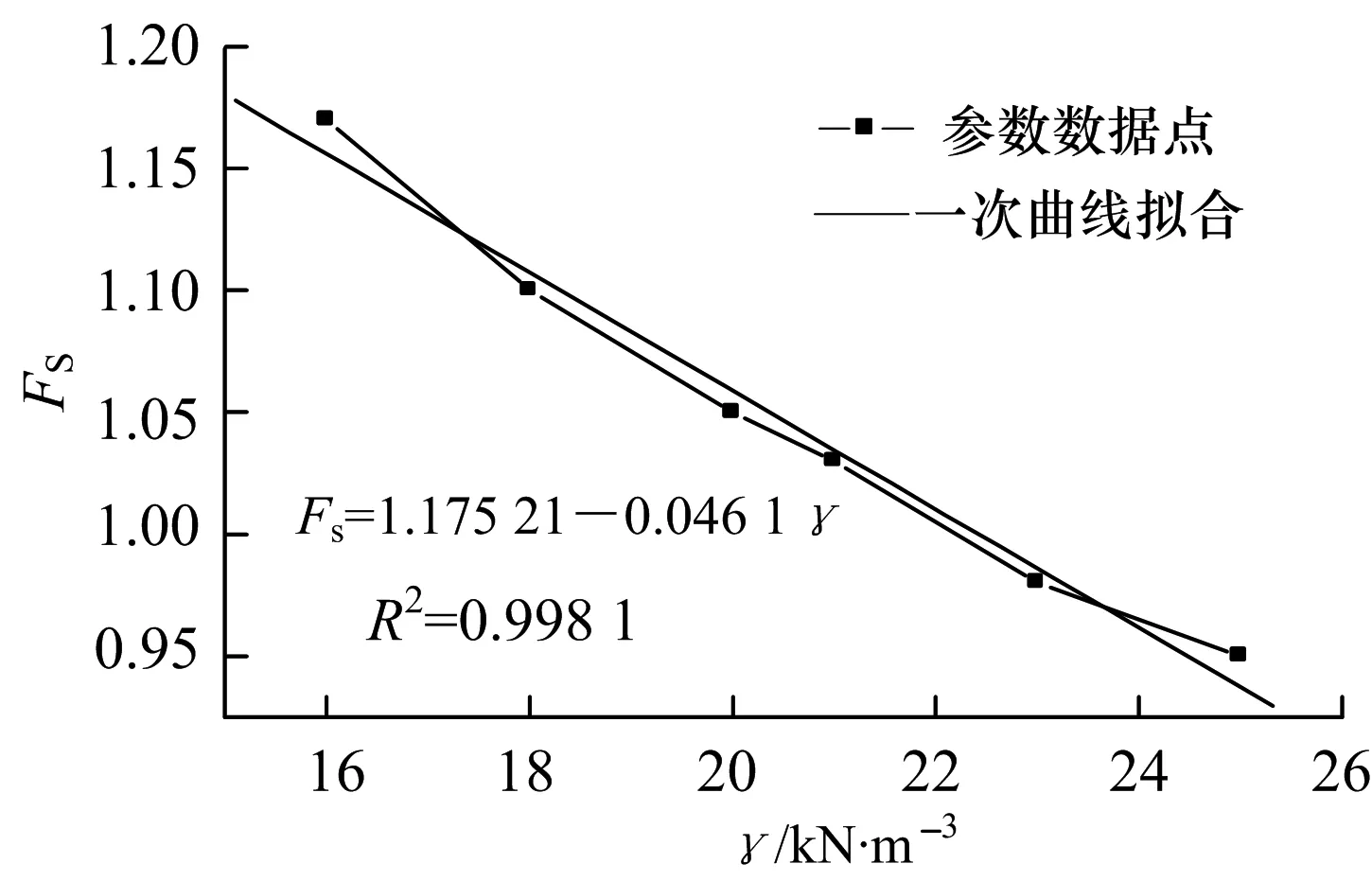
a) c=12.38 kPa

b) c=37.14 kPa

综上所述,在边坡稳定性的影响因素中,当内摩擦角固定时,土体重度与粘聚力的敏感性程度并无定性关系.当粘聚力较小时,土体重度对边坡稳定安全系数的敏感性小于粘聚力对边坡的敏感性,而当粘聚力较大时,土体重度对边坡稳定安全系数的敏感性大于粘聚力对边坡的敏感性.

3 结论

由于边坡岩土体的矿物、结构、状态等均随时间、空间而改变,其所反映的一些参数如粘聚力、内摩擦角、重度等多具有复杂多变的特点.当雨季来临时,土体的稳定性会大幅度下降,因此,分析影响边坡稳定的土体参数敏感性程度尤为重要.本文通过FLAC-3D有限差分法对影响边坡稳定性的岩土体参数进行敏感性分析,得到的结论如下:内摩擦角的敏感性最强,粘聚力和土体重度次之,与前人所得的结论相一致[5-7].但是土体重度与粘聚力对边坡稳定的敏感性的相互关系却与现有的研究结果存在一定差别[7],原因是FLAC-3D软件能够克服传统极限平衡法中的不足,能够有效地考虑变形、剪胀角等因素对边坡稳定的影响,故认为文中的结论更接近工程实际,可以作为边坡防治设计的有益借鉴.

References)

[1] 张新敏,蒋中明,刘建辉.公路滑坡滑带c、φ值反分析方法[J].中外公路,2005,25(5):24-26. Zhang Xinmin,Jiang Zhongming,Liu Jianhui. The inversing analysis method ofCandφon highway landslide zone[J].JournalofChina&ForeignHighway,2005,25(5):24-26.(in Chinese)

[2] 王家臣.边坡工程随机分析原理[M].北京:煤炭工业出版社,1996.

[3] 孙书伟,林杭,任连伟.FLAC-3D在岩土工程中的应用[M].中国水利水电出版社,2011.

[4] 陈育民,徐鼎平.FLAC/FALC-3D基础与工程实例[M].中国水利水电出版社,2008.

[5] 罗常青,陈征宙,李文勇,等.某加筋土边坡稳定性系数影响因素的敏感性分析[J].防灾减灾工程学报,2008(4):479-483. Luo Changqing, Chen Zhengyu, Li Wenyong,et al. Sensitivity analysis of stability coefficient influence factors on a reinforced soil slope[J].JournalofDisasterPreventionandMitigationEngineering, 2008(4):479-483.(in Chinese)

[6] 黄霞,谭鹏燕.敏感性分析在滑坡力学参数选取中的应用[J].重庆交通大学学报:自然科学版,2011,30(1):655-657. Huang Xia,Tan Pengyan. Application of sensitivity analysis in the selection of mechanical parameters of landslide[J].JournalofChongqingJiaotongUniversity:NaturalScience,2011,30(1):655-657.(in Chinese)

[7] 庞茂康,任光明,李冬芹，等.某滑坡滑带土强度参数的敏感性分析[J].水电能源科学,2010,28(10):47-50. Pang Maokang, Ren Guangming, Li Dongqin,et al. Sensitivity analysis of strength parameters of landslide slip zone[J].WaterResourcesandPower, 2010,28(10):47-50.(in Chinese)

(责任编辑： 贡洪殿)

Sensitivity analysis of factors influencing stability of slope by strength reduction method based on FLAC-3D

Mei Ling, Ji Peixiang, Zhang Taiyue

(School of Architecture and Civil Engineering,Jiangsu University of Science and Technology, Zhenjiang Jiangsu 212003, China)

A solution to the stability coefficient of slope is obtained by establishing a homogeneous soil slope model and using FLAC-3D software with the strength reduction method built in itself. The paper systematically studies the sensitivity factors of slope stability. The safety factor of slope stability and the plastic area are taken as the slope failure criterion. In order to find the relationship between the stability coefficient and the mechanical parameters of rock mass, and to find the most sensitive factor, only one parameter variable is changed. The results show that the sensitivity of the angle of internal friction is the highest, and cohesive strength and soil weight are less sensitive. There is no permanent quantitative relationship between cohesive strength and soil weight.

FLAC-3D; slope stability; sensitivity analysis

10.3969/j.issn.1673-4807.2014.03.004

2013-12-24

梅 岭(1982—)，男，博士,副教授，研究方向为边坡稳定性.E-mail:mling530@163.com

TU413

A

1673-4807(2014)03-0220-05