传输函数和平面波入射角对合成声场的影响

彭昌友 黄青华

（上海大学通信与信息工程学院，上海，200072）

引 言

随着音频技术的发展，人们不仅能够准确识别声源位置［1］，而且还可使用扬声器阵列在听音区域内营造声学场景。谱分法（Spectral division method，SDM）［2-3］是最近提出的一种新的合成声场方法。该方法首先对声场进行空间傅里叶变换，在波数域内推导合成声场的次源驱动函数，再根据次源和次源驱动函数合成声场。理想的次源分布是连续次源，而现实生活中的次源是扬声器，故需对连续次源分布进行空间抽样离散化，在空间放置离散的扬声器阵列。因而抽样过程产生混叠现象，相关文献提出了抗混叠条件［4-5］和抗混叠次源［6］。因此，在波数域内研究离散次源和离散驱动函数成为声场合成研究的重要内容。

本文分析了SDM合成平面波声场和推导次源驱动函数的过程，在波数域内对传输函数加矩形窗函数，消去传输函数的瞬逝部分，实现传输函数的修改。在平面波频率一定的情况下，离散次源合成平面波声场还与抗混叠频率大小有关，同时平面波入射角决定抗混叠频率的大小，因此提出了在波数域内联合传输函数和平面波入射角的方式分析其对合成声场的影响。仿真结果表明，修改的传输函数和较大的平面波入射角有利于合成理想声场。

1 线形次源合成的平面波声场

1.1 连续线形次源合成的平面波声场

声场合成系统目的是通过次源在听音区域内重现声学场景，这就要求分析合成声场的次源分布和找到合适的次源驱动函数［7］。现实中线形分布的扬声器能合成具有立体感的平面声场，如图1所示。

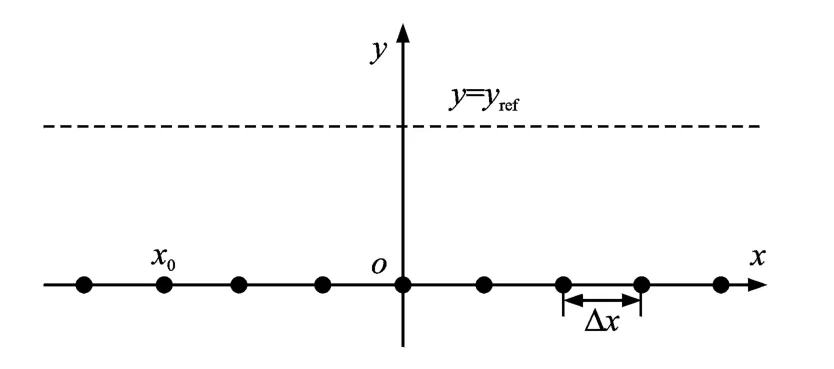
图1 线形次源分布Fig.1 Linear secondary source distribution

合成声场的次源分布在x坐标轴上，合成的声场可以表示为

式中：X0＝［x0，0，0］T为次源位置；X＝［x，y，0］T为xoy平面（（y＞0））的任意点位置；ω＝2πf为角频率；D（X0，ω）和G（X-X0，ω）分别为驱动函数和空间传输函数（三维格林函数）［8］。假设式（1）中次源具有全向性，即空间传输函数具有如下形式G｜y｜（x，y，z，ω）＝G｜y｜（x，-y，z，ω）＝G｜y｜（x，｜y｜，z，ω），那么合成的平面波声场相对于次源具有对称性，其表达式为

此时空间传输函数为

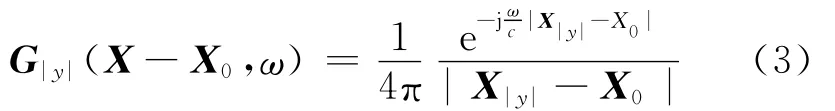
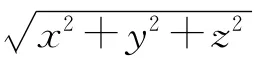
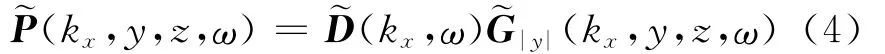
由式（4）可得次源驱动函数

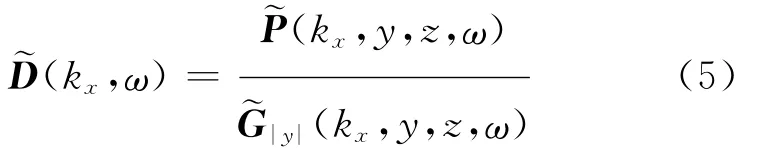
通过式（5）推导出驱动函数（kx，ω）的方法称为SDM，（kx，y，z，ω）是频率为fpw，传播方向为（θpw，αpw）的平面波声场，在波数域内的平面波和传输函数表达式｜y｜（kx，y，z，ω）见文献［2］，考虑合成声场在z＝0的水平面上，此时传输函数｜y｜（kx，y，0，ω）表达式为

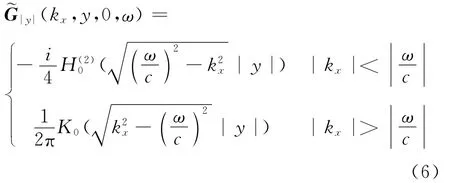
将（kx，y，z，ω）和式（6）代入式（5）得到驱动函数［2］

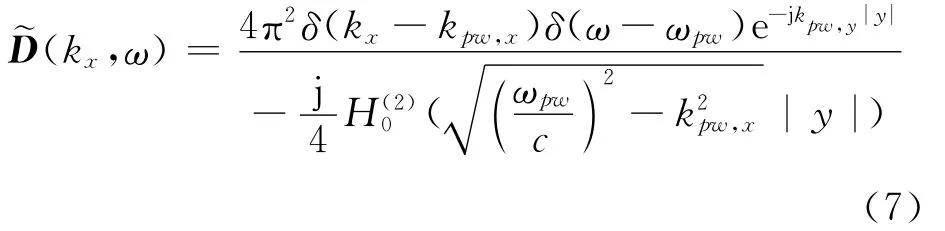
式中kpw＝ωpw/c，c是声音在空气中传播速度。在听音区内，文献［7］设｜y｜＝yref处到次源之间的区域能正确地合成声场，称｜y｜＝yref为合成声场的参考距离（见图1），kpw，x，kpw，y和已知频率ωpw关系为

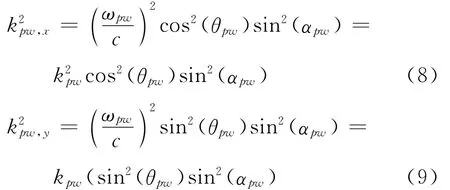
根据以上条件，可以得到次源的驱动函数

将式（10）和式（6）代入式（4），运用空间傅里叶反变换得到合成的声场为

由于连续次源未经过离散化，此时产生的声场为模拟声场，但实际生活中使用离散的扬声器阵列充当次源，故需要对连续次源的离散化进行分析。

1.2 离散线形次源合成的平面波声场

现实生活中使用离散的扬声器阵列合成声场，在理论分析时对次源抽样离散。设次源间隔为Δx，在空间离散位置放置扬声器，并且推导出相应的驱动函数。对驱动函数的抽样离散过程如图2所示。

图2 驱动函数的抽样和加窗的传输函数Fig.2 Sampling and windowing of driving function

抽样后的驱动函数表达式为

由传输函数式（6）和离散化后的驱动函数式（12）得到声场的表达式如式（13）所示。

传输函数在波数域内包含瞬逝部分和传播部分，由于传输函数的瞬逝部分离散化造成合成声场的不理想［7］。因此，尽可能消除传输函数的瞬逝部分，达到合成理想声场的目的。

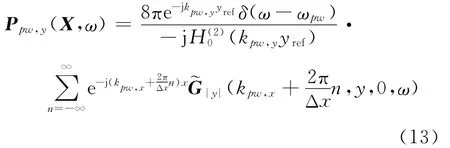
2 瞬逝声场的消除

2.1 传输函数的修改

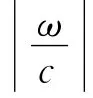
2.2 抗混叠频率与传输函数的组合

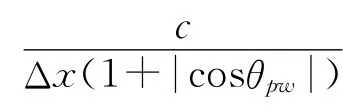
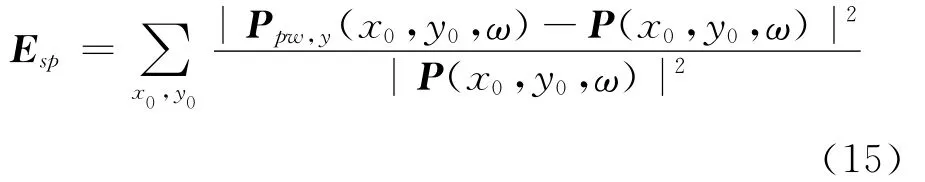
式中：（x0，y0）为声场中的各点的坐标；P（x0，y0，ω）表示点（x0，y0）理想平面波声场。通过这些不同的组合方式，综合分析传输函数的瞬逝部分与平面波入射角对合成平面波声场的影响。

3 仿真实验

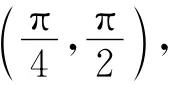
图3 线形次源合成的声场Fig.3 Sound field synthesized by linear secondary sources

对应于第2种组合方式，加上窗函数后的合成声场如图4所示，和图3（a）非抽样离散情况下合成的声场极相似，显然图4（a）合成的平面波声场优于图3（b）合成声场，即对传输函数加窗消除了部分瞬逝声场，提高了合成声场的效果。同时，经窗函数滤除的瞬逝部分合成的声场如图4（b）所示。

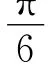
图4 入射角（θpw，αpw）＝合成的声场Fig.4 Synthesized sound field with incidence angle（θpw，αpw）＝

图5 入射角（θpw，αpw）＝合成的声场Fig.5 Synthesized sound field with incidence angle（θpw，αpw）＝

为了分析平面波频率在满足抗混叠情况下和平面波入射角对合成声场的影响，文中利用计算声场误差算法仿真了对传输函数加窗和不加窗两种情况下合成声场的误差图，如图6所示。

图6 传输函数加窗和不加窗时合成声场的误差Fig.6 Synthesized sound field error with modified transfer function and transfer function

4 结束语

本文分析了由连续线形次源和离散线形次源合成的平面波声场。针对传输函数中的瞬逝部分离散化对合成平面波声场的不利影响，提出了一种改进传输函数的方法，改进的传输函数减少了合成声场中的瞬逝声场，达到较好的效果。同时根据抗混叠频率大小对合成声场的影响，给出传输函数和抗混叠频率的组合方式。在平面波频率和离散次源间隔一定的情况下，加窗后的传输函数能消除传输函数的瞬逝部分，且当平面波频率满足抗混叠条件时，合成的声场较理想。当平面波频率不能满足抗混叠条件时，合成声场中存在混叠现象。文中没有分析扬声器间隔和平面波入射角的最佳结合取值对合成平面波声场的影响，以及在不满足抗混叠条件下，平面波入射角增大造成合成声场误差变大的原因，这些是今后研究的内容。

［1］陈少林，刘丽.基于波叠加方法的可视化声源识别［J］.南京航空航天大学学报，2008，40（6）：804-809.

Chen Shaolin，Liu Li.Acoustic source identification based on wave superposition method［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2008，40（6）：804-809.

［2］Ahrens J，Spors S.Reproduction of a plane-wave sound field using planar and linear arrays of loudspeakers［C］//3rd International Symposium on Communications，Control and Signal Processing（ISCCSP 2008）.［S.l.］：ISCCSP，2008：1486-1491.

［3］Ahrens J，Spors S.An analytical approach to local sound field synthesis using linear arrays of loudspeakers［C］//IEEE International Conference on Acoustics，Speech and Signal Processing.Prague：IEEE，2011：65-68.

［4］Start E W.Direct sound enhancement by wave field synthesis［D］.Delft：Delft University of Technology，1997.

［5］Spors S.Spatial aliasing artifacts produced by linear loudspeaker arrays used for wave field synthesis［C］//Second IEEE-EURASIP International Symposium on Control Communications and Signal Processing.Marrakech，Morocco，IEEE，2006：8-12.

［6］Ahrens J，Spors S.On the anti-aliasing loudspeaker for sound field synthesis employing linear and circular distributions of secondary sources［C］//129th convention of the AES.San Francisco：CA，2010：4-7.

［7］Ahrens J，Spors S.Sound field reproduction using planar and linear arrays of loudspeakers［J］.IEEE Trans on Sp and Audio Proc，2010，18（8）：2038-2050.

［8］陈晓东，陈心昭，陆益民，等.声全息重构卷积计算中混叠问题的研究［J］.数据采集与处理，2004，19（3）：346-351.

Chen Xiaodong，Chen Xinzhao，Lu Yimin，et al.Alias error in discrete convolution of reconstruction of near-field acoustical holography［J］.Journal of Date Acquisition and Processing，2004，19（3）：346-351.

［9］Ahrens J.The single-layer potential approach applied on sound field synthesis including cases of nonenclosing distributions of secondary sources［D］.Berlin：Technische University at Berlin，2010.

［10］Kamado N，Saruwatari H，Shikano K.Robust sound field reproduction integrating multi-point sound field control and wave field synthesis［C］//Acoustics，Speech and Signal Processing（ICASSP），2011IEEE International Conference on.Prague：［s.n.］，2011：441-444.