微积分及其在经济学中的应用

沈奇

（黑河学院 数学系，黑龙江 黑河 164300）

微积分及其在经济学中的应用

沈奇

（黑河学院 数学系，黑龙江 黑河 164300）

微积分的产生是数学发展史上一个重要的里程碑，在近代数学的发展中起到了重要的作用.微积分方法目前已被应用于各个学科领域.本文对微积分进行了简单的介绍，并对微积分在经济领域的边值问题、最值问题进行了相应的分析，给出了微分学和积分学在经济领域的应用实例.

微积分；边值问题；最值问题

1 微积分的产生及思想

“微积分”由微分学和积分学两部分组成，自17世纪以来，通过科学家们对不同领域的课题进行研究，使得微积分应运而生.微积分的产生通常可分为三个阶段：极限概念的产生；求积的无限小法（分割、求和、取极限）；积分和微分的互逆关.微积分的产生和发展构成了近代数学的主要内容，对数学的发展具有重要的意义.

微积分主要解决两类问题，即变化率问题（微分问题）和积累问题（积分问题）.解决变化率问题的思想是，考察在某个点附近的小范围内，近似的以“不变代变”、“以静代动”，求得平均变化率.该平均变化率近似等于该点处的瞬时变化率.再将小范围无限缩小而趋向于零，促使“近似”转化为“精确”，从而求得函数在指定点处的变化率.

积分问题的基本思想是，先将整体化为有限个微小的局部，在每个局部“以直代曲”、“以不变代变”，再积零为整求和式，得到整体的近似值，最后，再使每一局部无限变小，通过求和式极限，促使“近似”转化为“精确”,从而得到积累问题的准确值[1,2,3].

微积分的产生、发展与实际问题紧密相连，其思想为函数类型的判断、极值问题等提供了理论依据，并且在航海、天文学、物理学和经济学等领域得到了广泛地应用.

2 微分在经济学中的应用

2.1 微分在边际问题中的应用

边际问题是经济学研究的重要问题之一，比如边际成本、边际收入、边际利润等，在经济学角度看来都是十分重要的问题.

现假设经济函数y=f(x)，并且在定义域内是可微的，那么有：

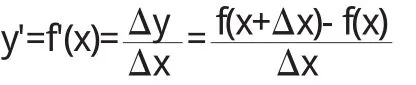
f'(x)称为函数f(x)的边际函数，表示因变量关于自变量的变化率，即经济变量的变化率.f'(x)在x0点处的函数值f'(x0)称为边际函数值，表示经济变量x在x=x0条件下改变一个单位，经济函数值改变f'(x0)个单位.因此，总成本函数的微分即为边际成本、总利润函数的微分就是边际利润，等等[4].

下面以边际成本为例，分析微分在边际问题中的应用.

设某企业生产某种产品，其产量为q，生产总成本为C，C是关于q的函数，且函数关系式为：C(q)=0.02q3+3q+200，那么边际函数为：C'(q)=0.06q2+3.

现假设产量为100，那么此时边际成本为：C'(100)=0. 06×1002+3=603，其经济意义表示当产量达到100时，若再增加一个单位的产量，总成本将会增加603，如果令产品的单位为p，当p>603时，此时扩大生产将会盈利；当p<603时，扩大生产将会导致亏损.

2.2 微分在最值问题中的应用

在自然科学、生产技术领域中，往往需要考虑如何在消耗最小的情况下，使得收益达到最大化的问题，在经济生产中，为了提高经济效益，这种关于优化的最值问题也是十分重要的.例如利润是衡量一个企业经济效益的重要因素，那么如何实现投入成本最低，而使得利润达到最大呢？这节将讨论在经济活动中的最值问题.

定理 设函数f(x)在x0点的某一邻域中有定义，f(x)在x0点连续且可导，若f'(x0)=0，且f(x)在x0点二阶可导，那么有：若f"(x0)<0，则x0是f(x)的极大值点.

对产品从生产到销售的过程进行核算时，都会涉及到成本、收益和利润的问题.设产量为q，则总成本为C通常为q的函数，一般表示为：

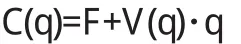
其中F>0为固定成本，通常认为与产量无关，为常数；V (q)·q为可变成本，V(q)是常值函数或常数，表示在生产q件产品的情况下，每生产一件产品的可变成本.设总收益为E(q)=p(q)·q，其中p(q)为价格函数，表示在生产q件产品的情况下，每件产品的销售价格.

由1中讨论可知C(q)、E'(q)分别为边际成本和边际收益，其经济学意义分别表示：在生产（销售）q件产品的情况下，再生产（销售）一件产品的成本（收入）.

令总利润函数为P(q)，那么有：

P(q)=E(q)-C(q)

当C(q)和E(q)的二阶导数存在时，要使得利润达到最大，由上述定理可知，应满足以下条件：

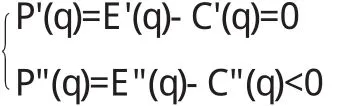
例 某产品的价格p(q)=α-βq（α,β>0,q<α/β），成本C(q) =F+vq（F,v为常数），那么利润P(q)=E(q)-C(q)=-βq2+(α-v)q-f,要使利润最大，即，则可得产量q=α-v02β（α-v>0保证企业盈利）.

3 积分在边值问题中的应用

在前面的讨论中，我们采用微分的方法求解由总函数求边值函数的问题.正如数学的角度一样，微分和积分是一对互逆的运算.本节我们将讨论用积分法求解由边值函数求解总函数的问题.

在经济问题中，通常会遇到对已知导数求原函数的问题，即求解常微分方程的问题.由边值函数求解总函数一般采用不定积分；如果要求总函数在某个范围的该变量，则采用定积分来求解.由于边际收益、边际成本、边际利润在产出量q的变动区间[α,β]上的增量等于它们各自边际在区间[α, β]上的定积分[5]，于是有:

例 设某产品的边际成本和边际收益为：C'(q)=0. 6q+10，E'(q)=30-0.2q

（1）产量由5增加到10时，总成本和总收益增加多少？

（2）已知固定成本为1万元，产量为多少时总利润最大，此时总利润、总成本和总收为多少？

解（1）产量由100增加到500时总成本与总收益的增加量分别为：

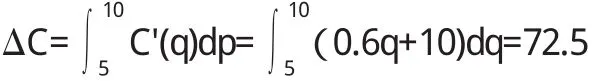
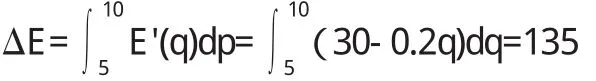
（2）由边际成本函数可得总成本函数：

由C(0)=1，代入上式得C=1，故总收益函数为

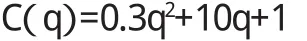
由边际效益可得总效益函数：

由E(0)=0，代入上式得C=0，故总收益函数为

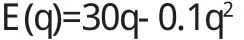
又由

可知，q=25时，总利润最大.此时，总利润、总成本和总收益分别为：

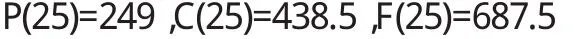
4 总结

在上述的讨论中，本文只对微积分在经济研究中的部分应用进行了相应的分析，而且，在经济领域中的很多类似的定量分析问题均可采用微积分的方法进行求解，微积分在经济研究中具有重要的作用.不仅如此，数学思想在经济学领域的应用，也使得金融数学学科得到了快速发展.利用数学思想对某些抽象的经济问题进行分析，可使问题简单化，易于理解.因此，将数学求解问题的方法应用到经济领域具有重要的意义.

〔1〕陈纪修，於崇华，金路.数学分析[M].北京：高等教育出版社，2004.

〔2〕马国良.微积分发展浅议[J].云南财经学院学报，2000.

〔3〕李万军.微积分思想及其认识[J].周口师范学院学报，2008.

〔4〕吴元芬.论微积分在经济分析中的应用[J].数学学习与研究，2010(15).

〔5〕谭瑞林，刘月芬.微积分在经济分析中的应用浅析[J].商场现代化，2008.

O172

A

1673-260X（2014）12-0006-02