分数阶微分方程积分边值问题正解的存在性探究
2014-07-25冉营丽孟琳琳
冉营丽,孟琳琳
(郑州华信学院 基础教学部,河南 郑州 451100)
分数阶微分方程积分边值问题正解的存在性探究
冉营丽,孟琳琳
(郑州华信学院 基础教学部,河南 郑州 451100)
本文针对分数阶微分方程积分边值问题正解的存在性问题进行了分析,希望所得结果能够引起大家的关注和重视.
分数阶微分方程;积分边值;问题正解存在性
0 引言
最近这些年,关于分数阶微分方程方面的问题逐渐成为许多专家和学者研究的热点话题.分数阶微分方程较多的应用在数学领域、流体流变学领域,其涉及到的理论知识十分复杂,关于分数阶微分方程解的存在性,很多专家和学者都进行了大量的研究和试验.
1 分数阶微分方程积分边值问题正解存在性研究的意义
在现实的问题当中,微分方程能够更准确的将化学、物理、生物等方面的问题做出合理的描述,而且在科学研究等领域,分数阶微分方程也具有十分广泛的应用.举个例子来说,在对扩音器进行反馈和分析的时候,都能够应用到这种理论[1].但是对于边值问题的提出和研究,主要是从应用物理和应用数学等领域得出的,除此之外,在热传导领域和流体学等领域对于分数阶方程积分边值的研究和应用也十分广泛.
2 微分方程边值问题的研究
2.1 边值问题的提出
给出一个微分方程:f(x,y,y',…,y(n))=0
在区间I上的点α1,α2,…,αk及值y(αi),y┡(αi),…,y(n-1)(αi)(i=1,2,…,k,k>1),对该方程设定一些条件,对于这个方程在I上面满足这些条件时候的边值和界值进行求解.
当该区间I的端点是K=2,α1、α2时,就能够证明,此时两点的边值问题.关于边值问题的提出涉及到了诸多的领域和学科,不仅仅与物理学有着密切的关系,而且也涉及到了材料力学、流体力学和波动力学.此外,边值问题在现代控制理论这一学科当中也具有重要的研究价值.常微分方程能够用来求解和进行解析的类型非常少,基于这点原因对边值问题进行求解也是具有相当难度的,但是为了适应实际问题的需要,采用近似求解也是一种不得已的方法.因此,我们首先需要回答这样一些问题:边值问题的解是否存在?是否惟一?这就是边值问题的基本论题[2].
2.2 分数阶微分方程积分边值问题的可解性研究
我们以射线法为例进行研究,选择一个微分方程的一般形式:

上述方程边值的条件主要有三个类型,其中第一类是:

第二类是:

第三类是:
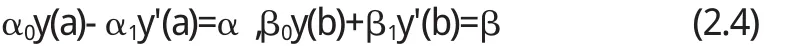
运用数值法对边值问题进行计算求解,求解之前需要在理论上进行验证,也就是说对边值问题的解是否合理进行解答.如果边值问题的解不存在,那么采用数值方法来对数据进行计算是没有意义的.所以,下面给出一个边值问题存在唯一解的充分条件,如下:



则边值问题(2.1)-(2.4)的解存在且唯一[3].
3 预备知识
假如二阶线性常微分方程边值存在解,并且是唯一正解,并定义出现行算子L:Ly=-y"+p(x)y'+q(x)y.
这样我们可以进行考虑,需要对两个线性微分方程初值问题进行合理的解释:
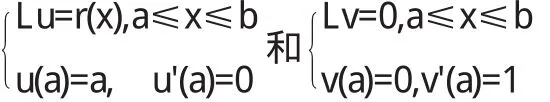
设u(x)和v(x)分别为上述两个问题的解,那么就不难验证是更上一个问题的解,其中v(b)≠0.
这样,通过以上的验证和描述,我们可以采用基于叠加原理的打靶式方法进行研究,该方法的主要步骤如下:
1.根据边值问题构造相应的初值问题;
2.分别求出两个初值问题的解,这里面为u(x)和v(x);
3.以上述问题为例,将u(x)和v(x)进行组合,最终所得到的函数y(x)就是上面边值问题的解.
u(x)和v(x)都是二阶常微分方程的初值问题,因此在进行求解的时候需要将变量代换引入进来,将这个问题进行转化,转化为与该方程相适应的一阶方程的初值问题就能够更好地解决.如令:

则该式可以写成
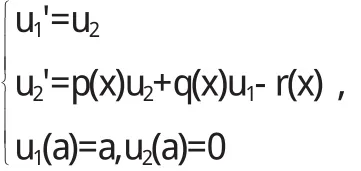
该式可以写成
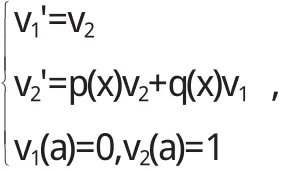
这样就可以利用Runge-Kutta方法求解.
对于更为普遍的线性边值问题:
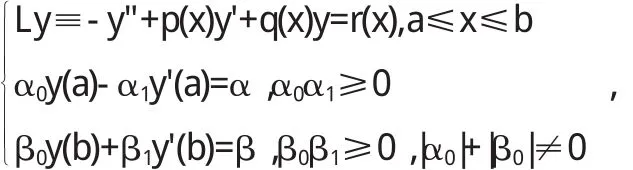
用基于叠加原理的打靶法的步骤为:
1.再重新构造一个方程,创造出两个与之相适应的处置问题:
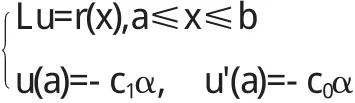
和
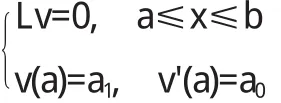
其中c0和c1是满足条件c1α1-c1α0=1的两个任意的常量[4].
2.对初值问题进行求解,设它们的解分别为u(x)和v(x).
由此计算得到的函数y(x)就是这个方程的解.
此外,再讲一个特殊方程的边值问题,我们将其称之为固有值问题,也有人称之为本证值问题.这是一个含参数λ齐次边值的问题,也就是说在这个方程里,无论是边界条件还是微分方程都是齐次的,所以保证齐次边值的问题具有非零解数值λ,就是特征值,对这些非零解本身就是一个特征函数,也可以称其为特征向量.
常型斯图姆-刘维尔问题(简称SL问题)是最典型的特征值问题:
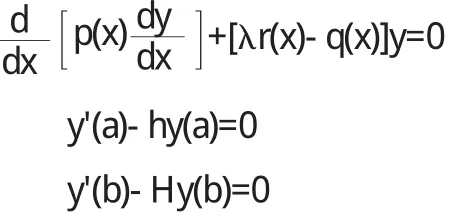
在上述式子中,(α,b)是一个有限区间,1/p(x),q(x),1/r(x)是实的有界连续函数.
常型问题一般都存在数不清的特征值,以λ0<λ1<λ2<…λn表示,每一个λn,都有一个对应的非零解yn(x),我们将其称之为特征函数.{yn(x)}组成(α,b)上的完备正交系.对任意函数f(x),有特征展开式
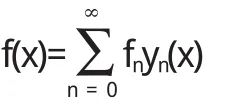
式中fn是f(x)的广义傅里叶系数,等于f(x)与yn(x)的乘积沿(α,b)的积分.当f(x)满足边界条件,且f┡(x)绝对连续时,展开式一致收敛.当f(x)平方可积时,展开式平方平均收敛.
斯图姆曾经证明了一个一般性的比较定理:如果g(x) 当(α,b)不是有限区间,或者1/p(x),q(x),1/r(x)中至少有一个不是有界连续时,就称微分方程为奇型SL方程.这样边界条件的体罚和展开形式相对来说就较为复杂.按照H.外尔的理论来说,对于某个复数λ,微分方程的任何解都在b点邻域平方可积,这样一来,b属于圆款;否则称b属于点款.而前面的方程,对于b点来说,需要提线性边界条件;而对于后面的方程,只提平方可积条件就可以了.若α点为奇点,也有同样的分类.当区间仅有一端为奇点,特征展开式为 式中 φ(x,λ)为满足α处边界条件的解;ρ(λ)为不减函数,称为谱函数.当ρ(λ)为纯阶梯函数时,展开式成为前述的级数形式(10),当ρ(λ)没有跳点,展开式成为广义傅里叶积分[5].对于区间两端都为奇点的情形,展开式为 式中[ρij(λ)]称为谱矩阵;φ1,φ2则是方程的线性无关解组. 4.1 当f(x)为pm(x)eλx与eλx[pl(x)cosωx+pn(x)sinωx]时,特解的形式及解法. 当f(x)为pm(x)eλx与eλx[pl(x)cosωx+pn(x)sinωx]时特解的不同形式. 二阶常系数非齐次线性微分方程的一般形式为 这里我们只讨论f(x)为pm(x)eλx与eλx[pl(x)cosωx+pn(x) sinωx]型. 4.1.1 f(x)=pm(x)eλx 利用待定系数法求通解. 据分析可设特解y*=Qm(x)eλx,推得y*=xkQm(x)eλx其中Qm(x)是与Pm(x)同次多项式.k按λ是特征方程的单根、重根,不是根可取为1、2、0. 例: 求下列方程的特解或通解. 4.1.2 f(x)=eλx[pl(x)cosωx+pn(x)sinωx] 利用上面结果及欧拉公式、性质推得 (1)当λ+iω是特征根时,k=1, (2)当λ+iω不是特征根时,k=0. 例: 求下列微分方程的特解 1.曲线上每点(x,y)处的切线在y轴上的截距为2xy2,且曲线过点(1,2),求此曲线方程. 解:设曲线的切线方程为Y-y=y'(X-x), 令X=0,于是切线在y轴上的截距为-xy'+y,从而 为贝努利方程,设u=y-1,上方程化为 其通解为,u=e-∫1xdx(∫2e∫1xdx d x+C)=x+C x 解: 方程两边对x求导,得 为一阶线性微分方程,解得 又因为f(x)|x-0=1,代入上式,得C=2,因此所求函数 解:方程两边对x求导,得f"(x)=6sin2x-f(x),即 此为二阶常系数线性齐次方程,其对应齐次方程的特征方程为r2+1=0,特征根为r1,2=±i,所以其对应齐次方程的通解为 且非齐次方程的右端函数为3(1-cos2x),2i不是特征根,所以非齐次方程的特解可设为y*=A+Bcos2x+Csin2x,代入原方程,比较系数得A=3,B=1,C=0,所以 于是原方程所求通解为又因f(0)=1,f'(0)=1,代入上式,求得C1=-4,C2=1,因此所求函数为f(x)=sinx-4cosx+cos2x+3. 在本研究当中,笔者主要针对微分方程边值问题正解的存在性问题进行了分析,同时研究了积分边值问题的非线性方程分数阶正解的存在性,从中可以得出,积分边值问题至少会存在一个正解,并且这是一个充分条件.通过本研究的论证可以得出,分数阶微分方程是存在正解的,但是关于正解的求法还需要更多的学者进行讨论和研究. 〔1〕高雷阜,王金希,吴洪涛.Banach空间中一类变分包含解的存在性和唯一性[J].辽宁工程技术大学学报(自然科学版),2012,14(02):154-155. 〔2〕夏顺友,黄南京.到锥度量空间上的半连续集值映射的连续性 [J].辽宁工程技术大学学报 (自然科学版),2012,11 (02):25-26. 〔3〕Hussein A.H. Salem. FRACTIONAL ORDER BOUNDARYVALUEPROBLEMWITHINTEGRALBOUNDARYCONDITIONSINVOLVING PETTIS INTEGRAL [J].Acta Mathematica Scientia. 2011,17(02):75. 〔4〕周昌宇,刘文斌.一类分数阶微分方程边值问题单调迭代解[J].黑龙江科技学院学报,2010,15(04):02-04. 〔5〕朱思念,王刚.一类非线性分数阶m点边值问题可数多正解的存在性[J].四川理工学院学报(自然科学版),2011,11 (03):24. O175 A 1673-260X(2014)12-0008-03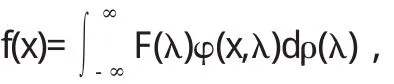

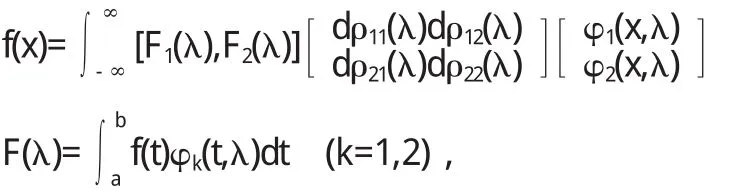
4 实际应用
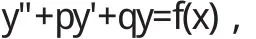


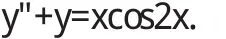
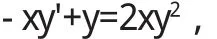
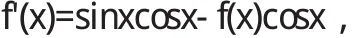
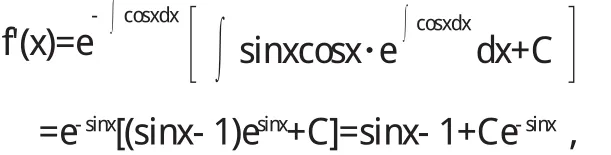
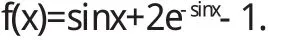
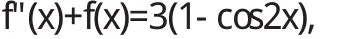
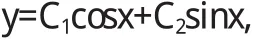

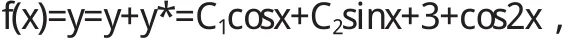
5 结语
