PEM燃料电池组装接触压力的有限元分析

刘永昌，胡学家，谈金祝，张晓维

（南京工业大学机械与动力工程学院，江苏南京210009）

PEM燃料电池组装接触压力的有限元分析

刘永昌，胡学家，谈金祝，张晓维

（南京工业大学机械与动力工程学院，江苏南京210009）

质子交换膜(proton exchangemembrane,PEM)燃料电池组装接触压力对燃料电池的性能至关重要。建立了包括燃料电池端板、电流收集器、双极板、垫片、气体扩散层(gas diffusion layer,GDL)、膜电极组件(membrane electrode assembly,MEA)和螺栓等在内完整的燃料电池三维有限元模型，采用有限元方法研究在不同组装力下PEM燃料电池的接触压力及其分布。有限元分析结果表明，燃料电池组装力增大，GDL与双极板以及MEA与GDL之间的接触压力也随之增大。组装力约为3.0 N·m时，燃料电池双极板与GDL之间的接触压力分布以及MEA与GDL之间的接触压力分布均具有较好的均匀性。

PEM燃料电池；组装力；接触压力；有限元方法

一个典型的质子交换膜(proton exchangemembrane,PEM)燃料电池由端板、电流收集器、双极板、垫片、气体扩散层(gas diffusion layer,GDL)和膜电极组件(membrane electrode assembly,MEA)等组成，这些部件通过螺栓组装在一起。在组装过程中，若组装力不足，燃料电池部件间接触压力过小，燃料电池不能很好地密封，导致反应气体泄漏，燃料电池界面接触电阻增加；若组装力过大，燃料电池接触压力过大，降低GDL的孔隙率，增大气体扩散阻力，损伤燃料电池的部件[1-2]。因此，在一定的组装外力下，PEM燃料电池部件间接触压力及其分布对燃料电池的电化学性能有重要影响。

有关组装力对燃料电池性能影响的研究有许多报道。Lee等[3]研究了分别采用三种不同的气体扩散层(ELAT，CARBEL和TORAY组合，TORAY)在三种组装力下的燃料电池电化学性能。Zhou等[4]利用数值模拟的方法研究了组装力作用下GDL变形对燃料电池的影响。Lee等[2]用数值模拟和实验的方法研究了燃料电池的组装对MEA和GDL接触状态以及接触压力的影响。李果等[5]针对PEM燃料电池中的双极板与气体扩散层，采用实验和有限元模拟相结合的方法研究螺栓夹紧力对接触电阻的影响。

尽管有一些文献报道了燃料电池组装行为以及组装力对燃料电池性能的影响，但有关PEM燃料电池组装接触压力及其分布的研究报道较少。本文以一台三通道蛇形流场PEM燃料电池为研究对象，采用有限元方法，研究在不同组装外力下，燃料电池GDL与双极板以及MEA与GDL之间的接触压力及其分布，采用统计学方法研究各部件之间的接触压力分布均匀性。

1 有限元模拟

1.1 几何模型及材料参数

本文采用三维有限元模型模拟单个燃料电池，其结构包括端板、电流收集器、双极板、密封垫片、螺栓、螺母、GDL以及MEA，在端板4个角以及边沿中间位置安装8个螺栓-螺母结构。双极板流场为蛇形流场，流道和脊的宽度均为1.2mm，流道深度0.6mm。各部件的几何尺寸见表1。由于燃料电池结构的对称性，取燃料电池结构的1/8建立有限元模型。燃料电池有限元分析几何模型见图1。

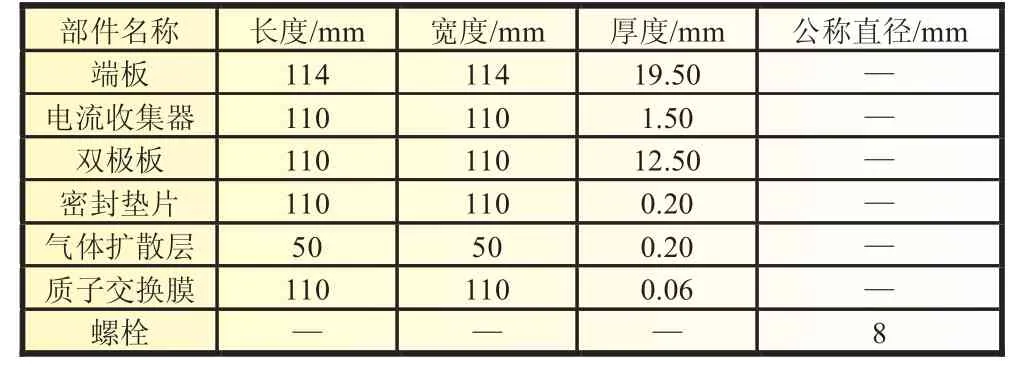
表1 各部件几何尺寸

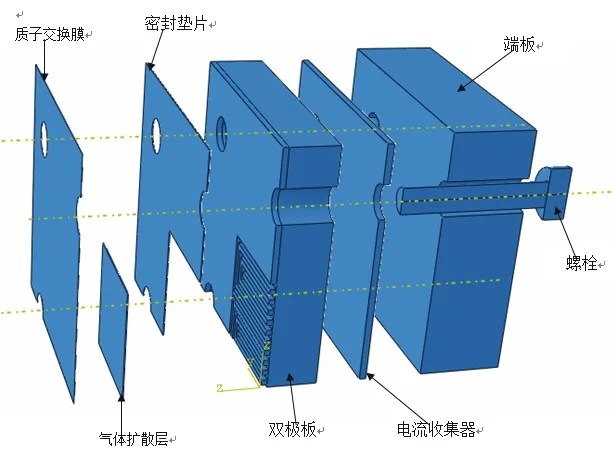
图1 PEM燃料电池结构示意图

燃料电池的PEM为美国DUPONT的Nafion212质子交换膜，GDL是日本TORAY公司的TGP-H-060碳纸，部分力学性能由商家提供，各部件的材料机械性能参数见表2。

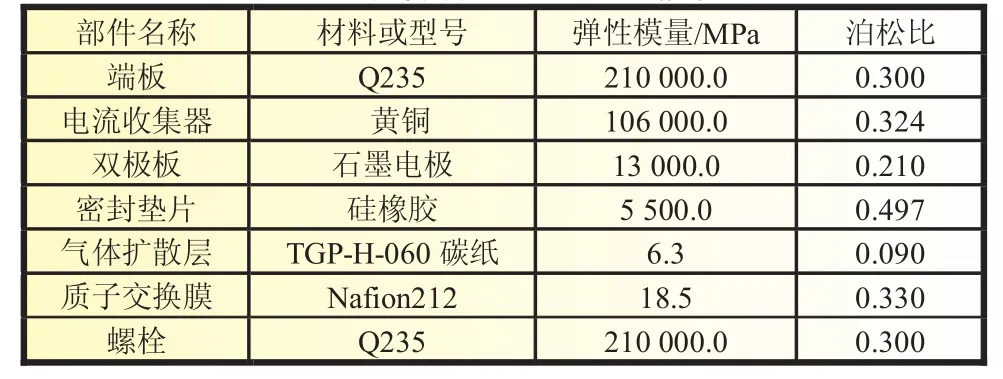
表2 各部件材料机械性能参数

1.2 网格划分

模型中所有部件均采用实体单元，单元类型为C3D8R，即八节点六面体线性缩减积分单元。线性缩减积分单元的优点是位移求解结果精确，即使网格扭曲变形时，分析精度都不会受太大影响，不容易发生剪切自锁现象[6]。GDL、MEA以及双极板流场部分是PEM燃料电池的关键部位，应将其网格局部细化，模型共划分为138445个单元，网格划分如图2所示。

1.3 边界条件及载荷施加

本文有限元分析模型为燃料电池结构的1/8，所以在其对称面上分别施加关于轴、轴、轴的对称边界条件。PEM燃料电池中各组件间的主要装配关系为接触装配关系。采用面对面算法定义端板与电流收集器、电流收集器与双极板、双极板与密封垫片、双极板与GDL、GDL与MEA、密封垫片与MEA、螺栓与端板的接触关系。忽略各个接触对之间的摩擦，全部采用无摩擦约束定义接触属性。

图2 模型网格划分

燃料电池每个螺栓上施加载荷为2.0～5.0 N·m，将所施加扭矩转化为螺栓力分别施加于螺栓上。螺栓力的施加如图3所示。

图3 施加螺栓力

2 结果分析

在不同的组装外力下，GDL与双极板接触压力的有限元分析结果见图4。图4(a)表示在施加组装外力为2.0 N·m时GDL与双极板接触压力的有限元分析结果，图4(b)表示在施加组装外力为5.0 N·m时GDL与双极板接触压力的有限元分析结果。图4中蓝色部分表示GDL与双极板流场流道接触区域，由于两个面的节点未发生接触关系，故其接触压力为零。由图4可以看出，GDL与双极板接触压力随着施加外力的增加而增加。

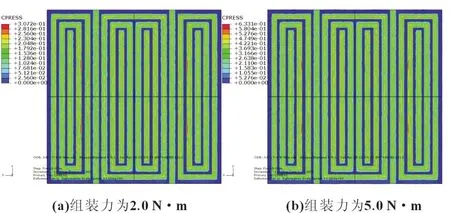
图4 气体扩散层与双极板的接触压力分布

为了进一步分析GDL与双极板接触压力分布情况，本文采用统计学方法中的平均值和标准差来分析GDL与双极板接触区域上的接触压力。

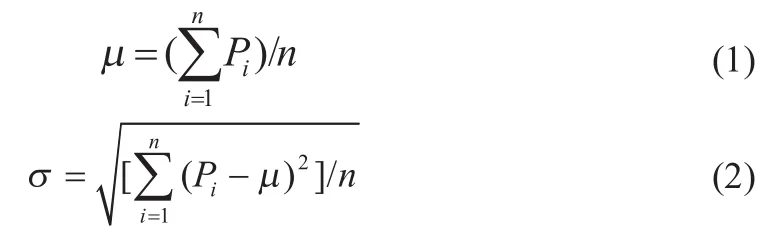
为了分析双极板流场脊与GDL接触区域上的接触压力分布规律，取GDL上接触压力大于零的所有节点(即双极板流场脊与GDL接触区域的所有节点)，共6630个。接触压力平均值及标准差见表3。

表3 气体扩散层与双极板的接触压力均值及标准差

从表3可以看出，GDL与双极板的接触压力平均值随着组装力的增加而增大；接触压力的标准差随着组装力的增大，呈先减小后增大的趋势。其中，当组装力为2.5和3.0 N·m时，接触压力的均匀性差别微小。由此可见，在2.5～3.0 N·m之间，存在一个使GDL上接触压力分布较均匀的组装力。

图5为MEA与GDL的接触压力有限元分析结果，图5 (a)表示在施加组装外力为2.0 N·m时MEA与GDL接触压力的有限元分析结果，图5(b)表示在施加组装外力为5.0 N·m时MEA与GDL接触压力的有限元分析结果。从图5中可以看出，浅蓝色部分为流场脊，接触压力较大，MEA与GDL的接触压力随着施加外力的增加而增加。MEA与GDL的接触压力平均值及标准差见表4。

图5 膜电极组件与气体扩散层的接触压力分布

从表4可以看出，MEA上的接触压力平均值随着组装力的增加而增大；接触压力的标准差随着组装力的增大，呈先减小后增大的趋势。其中，当组装力为3.0和3.5 N·m时，接触压力的标准差很接近且较小，这表明组装力在3.0～3.5 N·m时，MEA与GDL之间的接触压力较均匀。

表4 膜电极组件与气体扩散层的接触压力均值及标准差

为了分析在各种组装外力下GDL与双极板以及MEA与GDL之间的接触压力分布均匀性，将表3和表4中的数据绘于图6。由图6可以清楚地看到，组装力大约在3.0 N·m时，燃料电池双极板与GDL之间的接触压力分布以及MEA与GDL之间的接触压力分布均具有较好的均匀性。

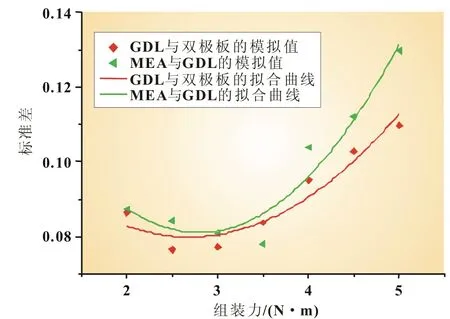
图6 接触压力标准差与组装力的拟合曲线

3 结论

采用三维有限元方法对PEM燃料电池进行有限元分析，在不同组装力作用下，研究了GDL与双极板之间以及GDL与MEA之间的接触压力及其分布，结果表明：

（1）考虑PEM燃料电池中各组件间的接触装配关系和接触属性，建立了包括端板、电流收集器、双极板、垫片、GDL、MEA和螺栓等在内完整的燃料电池三维有限元模型。

（2）组装力对GDL和MEA上的接触压力及其分布均匀性有显著影响，组装力增大，燃料电池部件之间的接触压力也随之增大。

（3）燃料电池组装过程中存在一个最佳组装力，从而使燃料电池GDL和MEA上接触压力分布最佳。本研究中组装力约为3.0 N·m时，GDL与双极板之间的接触压力分布以及MEA与GDL之间的接触压力分布都具有较佳的均匀性。

[1]LAI X M,LIU DA,PENG L F,et al.Amechanical-electrical finite elementmethodmodel for predicting contact resistance between bipolar plate and gas diffusion layer in PEM fuel cells[J].Journal of Power Sources,2008,182:153-159.

[2]LEE S J,HSU C D,HUANG C H.Analyses of the fuel cell stack assembly pressure[J].Journal of Power Sources,2005,145:353-361.

[3]LEE W K,HO C H,VAN Z J W,et al.The effects of compression and gas diffusion layers on the performance of a PEM fuel cell[J]. Journal of Power Sources,1999,84:45-51.

[4]LIM C,WANG C Y.Development ofhigh-power electrodes for a liquid-feed directmethanol fuel cell[J].Journal of Power Sources, 2003,113(1):145-150.

[5]李果，谈金祝，巩建鸣.PEM燃料电池双极板与气体扩散层界面接触电阻测量与模拟[J].机械工程学报，2011，47(8)：158-162.

[6]石亦平，周玉蓉.ABAQUS有限元分析实例详解[M].北京：机械工业出版社，2006.

Finite element analysis of assembly contact pressure in PEM fuel cell

LIU Yong-chang,HU Xue-jia,TAN Jin-zhu,ZHANG Xiao-wei

The contact pressure for proton exchangemembrane(PEM)fuel cell assembly was critical to the performance of the PEM fuel cell.A 3-dimensional finite elementmodel was built for the PEM fuel cell,including end plates,current collectors,bipolar plates,gaskets,gas diffusion layers(GDLs),membrane electrode assembly(MEA) and bolts.Using finite elementmethod,the contact pressure as well as pressure distribution were studied for the PEM fuel cell applied with various assembly forces.The finite element analysis results show that the contact pressures between GDL and bipolar plate and the GDL and MEA in the PEM fuel cell are increased with the increase of assembly force.It is found that the contact pressure distribution both between GDL and bipolar plate and between GDL and MEAhad the good uniformity as the PEM fuel cell was applied with the assembly force of about 3.0 N·m in this study.

PEM fuel cell;assembly force;contact pressure;finite elementmethod

TM 911.4

A

1002-087 X(2014)10-1818-03

2014-03-12

国家自然科学基金(51175241)；江苏省自然科学基金(BK2009362)

刘永昌(1984—)，男，河北省人，硕士研究生，主要研究方向为新能源技术。

谈金祝(1964—)，男，江苏省人，教授，主要研究方向为新能源技术及装备。