一种粗糙集遗传算法在入侵检测中的应用*
2014-07-25李锋
李锋
(广东交通职业技术学院,广东 广州 510650)
随着信息技术和网络的发展及应用,安全问题日益突出。入侵检测系统作为继防火墙后第二道安全防线,已成为保障网络安全的重要核心技术[1]。传统基于聚类的检测方法对数据输入顺序敏感,需要事先指定聚类数目等,造成聚类结果不理想,难以形成入侵特征,并且收敛速度慢,检测率不高。本文提出一种基于粗糙集的遗传算法并应用于入侵检测系统之中,通过粗糙集属性精简运算,降低算法时空复杂度。
1 入侵检测系统及其分类
1.1 入侵检测系统
入侵检测系统是一种主动防御体系,它从计算机系统或网络环境中采集分析数据,通过检测引擎判断可疑攻击和异常事件,在计算机网络和系统受到危害之前拦截特征行为攻击[2]。系统遭受入侵后,IDS能将收集到的入侵行为和相关信息纳入知识库,通过主动学习方式避免重复或类似攻击,有效弥补防火墙被动防御的不足。
1.2 入侵检测分类
入侵检测系统根据检测技术可以为分特征检测和异常检两类。特征检测是通过监视特定活动并与预先所设置的模式进行匹配来检测入侵[2]。这种利用特征库检测已知入侵行为的方法检测率高,速度快,并且对检测结果有明确的处理参照,但是不能检测未知攻击,很难将具体入侵手段抽象成知识特征。异常检测是基于系统或用户的正常行为模式检测入侵。该方法首先建立用户正常行为模式,当系统运行时将实时行为与正常行为模式进行匹配,一旦发生显著偏离即认为是入侵[2]。异常检测方式与系统环境无关,通用性较好,可以检测未知攻击和潜在威胁,但需要对每个户行为作全面描述,兼之个体行为的不确定性和独特性导致算法复杂,检测速度缓慢,漏报、误报率较高。
2 粗糙集理论
粗糙集理论是处理不精确、不确定和不完整数据的数学理论,能够对不一致、不完整、不完善信息提炼内在特征,揭示隐含规律。
粗糙集理论可以对决策表的属性进行约简,以便提高分类性能,获取潜在规则。对于任意决策表,不是每个属性对分类决策表的分类能力都有效,因此,在决策表分类能力不变的情况下,删掉冗余的条件或者决策属性,可以得到相对简单、易理解、易操作的决策表[3]。通过粗糙集理论对决策表属性进行约简,有利于过滤典型分类属性,形成新的决策表。通过约简决策表中的无关属性可以有效降低计算的时空复杂度,加速算法收敛。粗糙集理论如下。
表1给出一个简单的决策系统,包含 a、b、c、d 4个条件属性和一个决策属性e,隶属于8个目标对象。
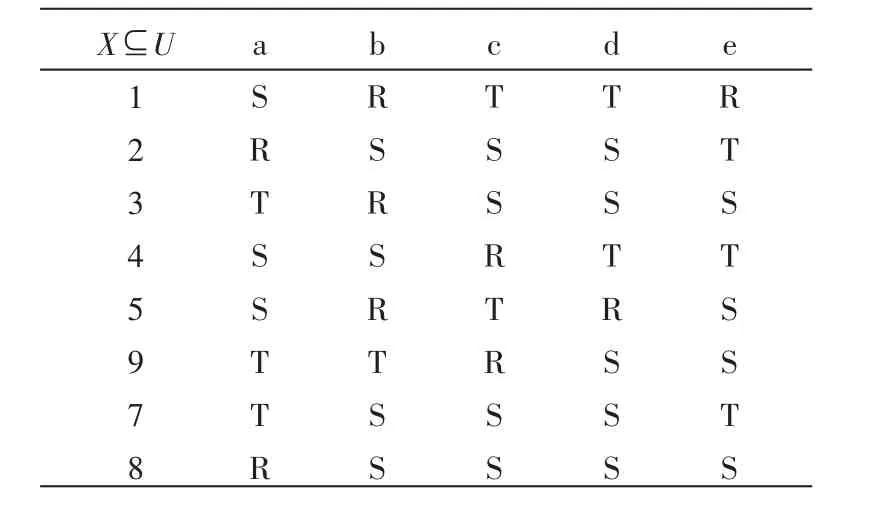
表1 决策系统
令X⊆U,在属性集合P中用P上近似和P下近似对集合X进行近似分类,分别用和表示P的上下近似值,表示如下:

((X),(X))所在区间称为粗糙集,如图 1 所示。图中每个方格表示一个等价类,通过等价类可以构建集合X的上下近似区域,位于P下近似内的等价类可以确定它们属于集合X。
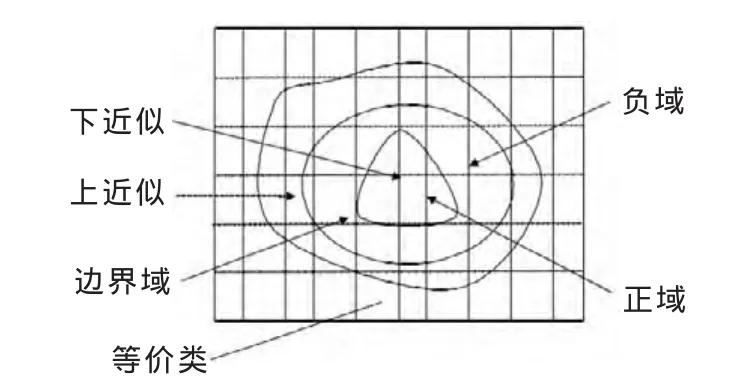
图1 粗糙集示意图
令P和Q是论域U中的等价关系,Q的P正域记为POSP(Q),负域为 NEGP(Q),边界域为 BNDP(Q),有如下关系:
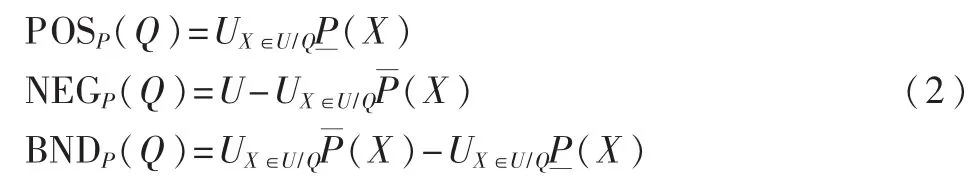
根据表1 决策系统,令P={b,c},令Q={e},按式(2)分别可以算出{e}的{b,c}正域、负域和边界域:

从计算结果可以得出,对象 3、4、6能够被{b,c}划分为{e}所确定的类别,分别是R、S和 T,而其他对象不能明确地分类,因为{b,c}对其对象不可分辨。
3 遗传算法
遗传算法 GA(Genetic Algorithms)源于达尔文的进化论和孟德尔、摩根的遗传学理论,由美国John Holland教授于20世纪60年代末提出,模拟生物遗传机制“适者生存、优胜劣汰”。遗传算法操作对象是一群二进制串,称为染色体或种群,每个染色体都对应于问题的一个解。从初始种群出发,采用基于适应度比例的选择策略在当前种群中选择个体,通过交叉选择和变异操作产生新一代适应度更高的染色体,重复上述繁衍进化过程直到收敛到一个最合适的染色体上,从而找出问题的最优解。遗传算法拥有卓越的智能学习效率和自适应性,近年来应用于故障诊断、行为仿真和入侵检测等领域。
决定遗传算法性能的3个参数分别为群体大小pop、交叉概率pc和变异概率pm。群体大小pop太小时难以找出最优解,太大则增加收敛时间;交叉概率pc太小时难以向前搜索,太大则容易破坏高适应值的结构;变异概率pm太小难以产生新的基因结构,太大使遗传算法成了单纯的随机搜索。
4 一种基于粗糙集遗传算法
粗糙集理论和遗传算法各有优势。粗糙集适用于主动学习模式,通过约简高维数据属性维数降低算法时空复杂度。而遗传算法处理数据量不大时具有良好的收敛性和鲁棒性,但在处理海量数据时,特别是当处理高维数据时,参数难以界定,易出现染色体的变异交叉操作使得算法经高次迭代繁衍仍无法收敛的问题。
本文将粗糙集约简原理与遗传算法进行整合,通过自适应学习方式为入侵检测系统提供行为特征。基本思想是通过粗糙集约简策略先过滤数据流量的无关属性,然后对处理后数据采用结合邻域思想进行分类,为遗传算法初始化种群,并保证筛选样本的稳定性和典型性,避免遗传算法处理数据量过大难以收敛的问题,最后由遗传算法迭代完成入侵行为特征的提炼和描述。
4.1 算法思想和流程
粗糙集的属性约简原理适合于处理精确数据,进行数据知识分类与获取,同时对决策分析进行辅助。经过粗糙集属性约简后的系统,属性的减少降低了计算的复杂性,但仍能够保持相同的决策要求和效果。遗传算法对数据特征进行选择和优化建立在选择合适的适应度函数以及合理进行选择、交叉和变异的基础上。
另外在遗传算法中,交叉变异算子作用是将群体中优良个体遗传到下一代,加速算法的收敛速度,并增加和维持群体多样性,以免陷入局部最优解的问题。但是传统算法中,交叉变异算子以一个极小概率随机改变染色体某些字位,随意性和任意性影响算法的收敛速度。本文再次利用粗糙集约简属性,将优异个体朝重要属性加速变异,并将其基因繁衍给下一代个体,以此改善遗传算法进行随机选择的不足,优化算法收敛速度。算法流程如图2所示。
4.2 算法实现步骤
(1)对网络流量进行二进制编码。
(2)用粗糙集理论寻找重要属性。
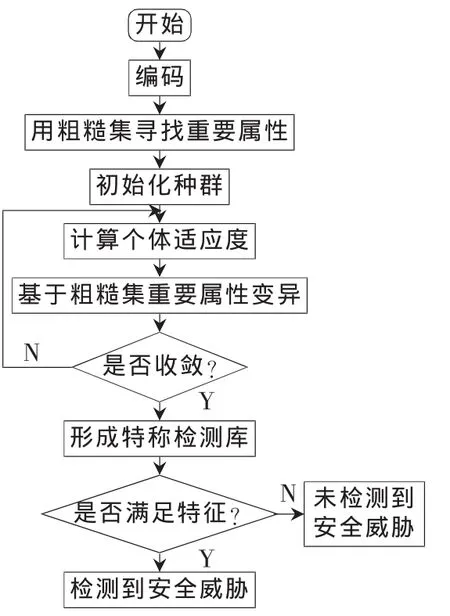
图2 新算法流程图
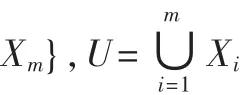
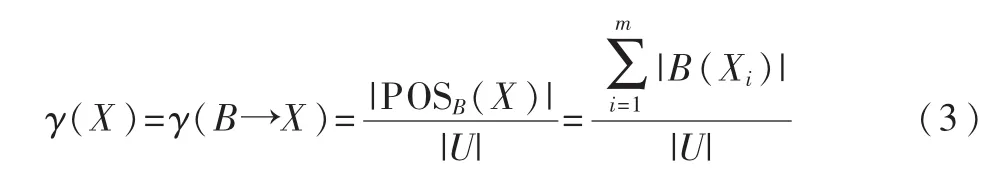
其中,γ(X)表示属性子集B对属性X的依赖度。
②若B⊆A满足 γB(X)=γA(X),称B是 A 的一个约简,记为 redx(A)。
③所有约简子集的交集,记作:

在分类方法中,邻域作为划分类别的判别标准。
④对于X上的任意对象Xi,其邻域表示为:δ(Xi)={X|Δ(X,Xi)≤δ}且 δ≥0,δ(Xi)称为Xi的邻域粒子。其中Δ是一个度量函数,它满足对于任意的Xi、Xj和Xk,重要属性需满足以下条件:
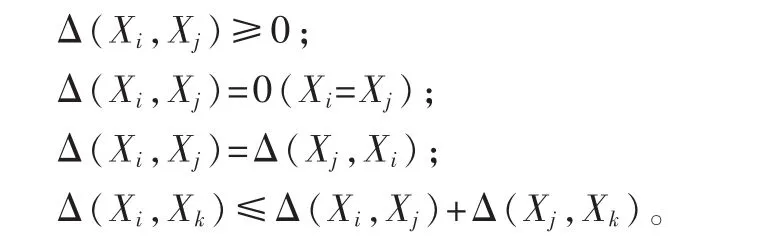
(3)初始化种群。属性占有数为M的染色体作为初代种群,产生初始种群N={N1,N2,…,Ni},适应度分别为N1,N2,…,Ni。
(4)计算平均适应度为:

(5)适应度函数的选择:
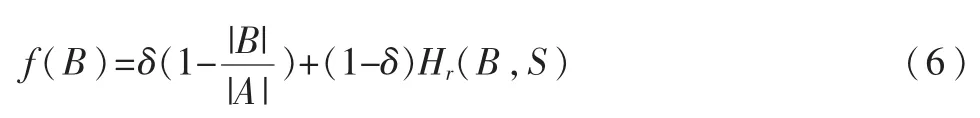
其中,|A|是原始数据集属性个数;|B|是遗传算法中染色体二进制串中的“1”的个数,即属性占有数;Hr(B,s)为染色体命中率。
(6)选取大于平均适应度的染色体个体是正常个体,设异常个体适应度为A,正常个体适应度为B,将适应度函数定义为{A,B}两类。
(7)根据步骤(2)过滤的属性构建信息数据表,其中,N={N1,N2,…,Ni}为 论域,Ni={X1,X2,X3,…,Xi}表 示第i条染色体;Xi表示第i种基因,即网络中的位置为i的网络连接数据;C为条件属性集;D为决策属性。
(8)以概率Pm对染色体依照信息数据表中的重要属性进行变异操作。
(9)把经过遗传算法迭代收敛后得到的染色体都放入池中,重新计算染色体适应度值,将满足重要属性的优良特征加入入侵特征库,并以此检测攻击行为。
5 实验测试
5.1 新算法检测率测试
新算法对基核函数的3个参数和NIDS试验数据的32个特征进行测试。编码方式采用n位参数编码加上32位的特征编码,组成64位联合优化编码。混合优化中遗传算法参数设置如下:初始化群体大小为300,最大遗传代数为2 000,变异概率为0.25,交叉概率为0.92,参数测试结果如表 2所示。
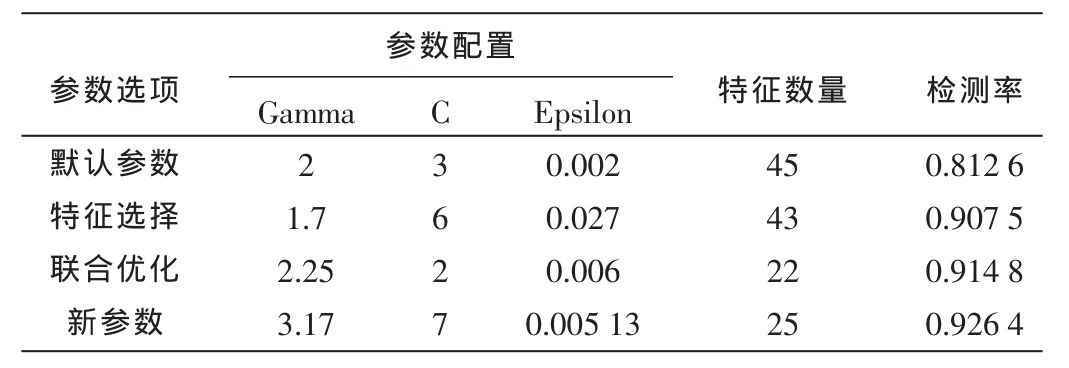
表2 新算法参数测试
5.2 新算法在入侵检测中的测试
本文数据集取自KDD99数据训练样本集中的513 021个样本,每个样本包括41个条件属性,1个决策属性,其中有34个属性值是数值类型,4个属性值是二元变量类型,其余4个属性值为标称类型[4]。分别从该数据集中分别选取5 000和10 000个数据为训练样本,经MATLAB 7.0处理工具将标称类型数字化。为验证新算法的有效性,本文采取表2中的新参数,并与遗传算法(GA)、遗传算法改进支持向量机(GA-SVM)进行比较[5-12],实验结果如表3所示。
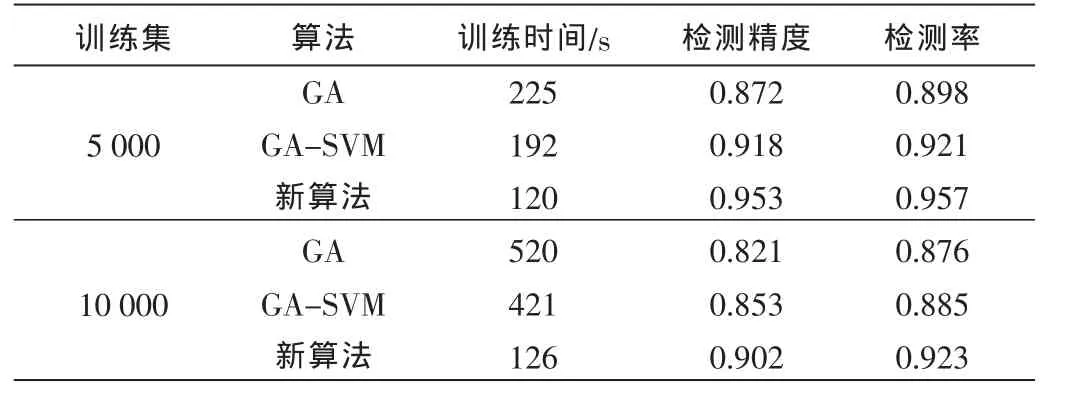
表3 3种算法测试数据表
新算法通过粗糙集理论约简属性,一方面为遗传算法提供初始化种群,减少训练时间;另一方面可避免随机变异造成的缓慢收敛,减少算法时空复杂度,随着样本的增多,新算法在训练时间上更具优势。在检测精度和检测率方面,新算法有效去除无用样本和冗余属性,检测更为方便快捷,检测精度和检测率都有不错表现。
5.3 个体适应度和迭代次数测试
新算法个体适应度明显优于其余两种算法。新算法利用粗糙集约简属性,将优异个体朝重要属性加速变异,并将其基因繁衍给下一代个体,使得个体适应度更高,新算法在第640次迭代已趋于收敛,如图3所示。而其余两种算法由于变异的随机性和任意性,适应度不高,分别在经760次和740次迭代才趋于收敛。
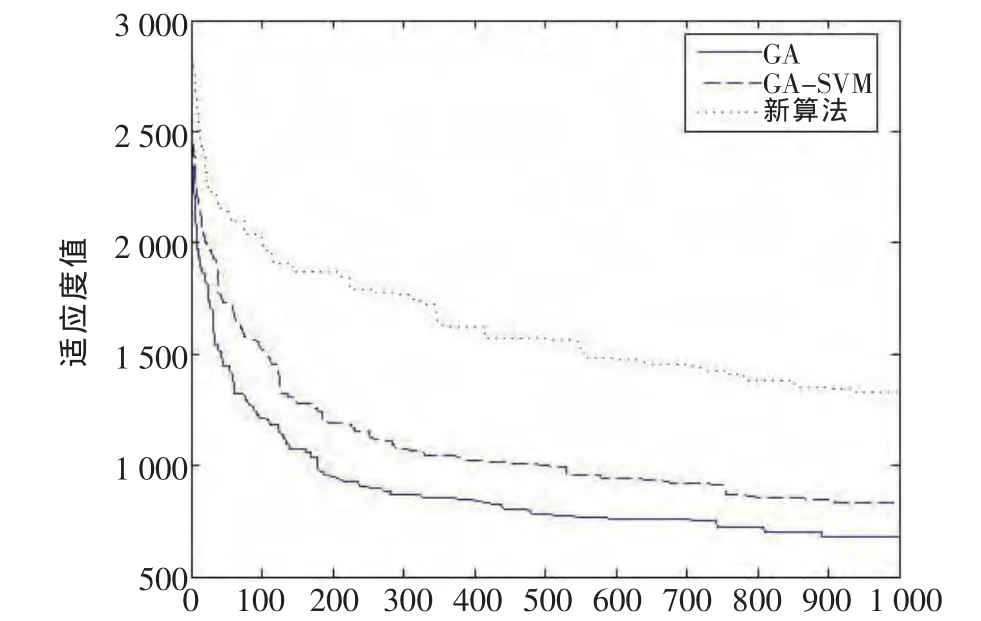
图3 个体适应度和迭代次数测试图
5.4 种群占重要属性比例趋势
新算法在变异操作中将优异个体朝重要属性加速变异并繁衍给下一代个体,种群占重要属性比例在500次迭代后呈指数上升,在630次迭代达到峰值,如图4所示,测试结果与图3数据相吻合。其余两种算法由于变异操作的不确定性,种群占重要属性比例在800次迭代前几乎呈线性关系,并且达不到峰值,这表明新算法能切实提高个体适应度,加快向优异群体变异速度,保持物种优势。
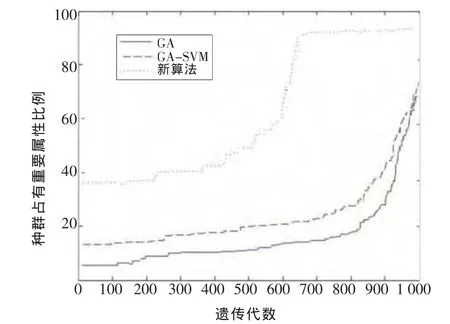
图4 种群占重要属性比例图
本文在研究粗糙集和遗传算法的理论基础上,提出一种基于粗糙集的遗传算法,通过粗糙集属性精简遗传算法种群,并在变异操作中将优异个体朝重要属性加速变异,降低算法时空复杂度。通过算法对比和实验分析,本文提出的新算法在提高网络入侵检测速度和准确率方面是有效的、可靠的和可行的,为网络安全信息建设提供强有力的保障。
[1]HOFMEYR S A,FORREST S.Architecture for an artificial immune system[J].Evolutionary Computation Journal, 2000,8(4):443-473.
[2]TSUI J B.Fundamentals of global positioning system receivers:a software approach[M].New York: Wiley, 2000.
[3]HOFMEYR S,FORREST S.Architecture for an artificial immune system[J].Evolutionary Computation, 2000,8(4):443-473.
[4]TARAKANOV A,DASGUPTA D.A formal model of an artificial immune system[J].BioSystems, 2000,55(55):151-158.
[5]BEHDINAN N A K,FAWAZ Z.Applicability and viability ofa GA based finite elementanalysis architecture for structural design optimization[J].Computers and Structures,2003,81(22-23):2259-2271.
[6]MIDDLEMISS M,DICK G.Feature selection of intrusion detection data using a hybrid genetic algorithm/KNN approach[C].Design and Application of Hybrid Intelligent Systems, IOS Press Amsterdam,2003:519-527.
[7]KWON Y, KWON S, JIN S, et al.Convergence enhanced genetic algorithm with successive zooming method for solving continuousoptimization problems[J].Computers and Structures,2003, 81 (17) :1715-1725.
[8]HUSSEIN O,SAADAWI T.Ant routing algorithm for mobile ad-hoc networks (ARAMA)[C].Proceedings of the 2003 IEEE International Conference on Performance, Computing,and Communications, 2003:281-290.
[9]ONDREJ HRSTKA,ANNA KUCEROVA.Improvements of real coded genetic algorithms based on differential operators preventing premature convergence[J].Advances in Engineering Software, 2004(35):237-246.
[10]KABREDE H,HENTSCHKE R.Improved genetic algorithm for global optimization and its application to sodium chloride clusters[J].Journal of Physical Chemistry B, 2002,106 (39) :10089-10095.
[11]HEISSENB U M,BRAUN T.Ants based routing in large scale mobile ad-hoc networks[C].Proceedings of the 13th ITG/GI-Fachta-gung Kommunikation Inverteilten System(KiVS2003), 2003:181-190.
[12]TIMMISJ, NEALM, HUNT J.Anartificialimmune system for data analysis[J].BioSystems, 2000,55,(55):143-150.
