混沌粒子群优化算法在柴油排产中的应用

姚明

（广东石油化工学院 计算机科学与技术系，广东 茂名 525000）

加氢精制是炼油厂广泛采用的加工过程，主要用于柴油的精制等。油品调合则是将各种柴油组分油以一定的比例混合，使油品质量符合国家标准。参与调合的柴油组分以及各组分的比例，需要根据各组分的性质、产品质量要求以及具体生产实际而定。在追求最低生产成本方面，产品性质与生产成本相互制约，通过加氢精制与调合优化可以解决这一问题。但油品调合存在着组分油种类多、目标多样化以及过程不可终止等限制条件，采用传统的计算方法如一些常规线性算法会出现计算量巨大、结果失真等问题[1-2]。近年来已有了一些新的方法和手段用于柴油的精制与调合。其中，使用计算智能优化算法和技术，可以在求解时间和求解精度上取得平衡，较好地解决这些问题。

粒子群优化算法 PSO （Particle Swarm Optimization）是由Kennedy和Eberhart等人于1995年提出的一种全局搜索算法，同时也是一种模拟自然界的生物活动以及群体智能的随机搜索算法，具有容易实现、应用领域广泛等优点。利用混沌独特的性质，将其引入到粒子群中，可有效提高现有粒子群算法的优化性能，解决粒子群算法易陷入局部极值的不足问题。目前已有不少混沌粒子群优化算法的成功应用[2-4]。本文根据某炼油厂柴油生产需求，建立了加工成本和库存成本优化模型，并使用设计的混沌粒子群算法进行实例计算，得到了较优的结果。

1 模型建立

柴油生产过程中降低成本的主要手段是在出厂柴油满足含硫量等质量指标要求的前提下降低高成本组分（包括调合和加氢柴油）的比例。同时，还要考虑原油的库存成本，降低高库存成本率组分油的库存。

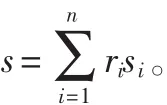
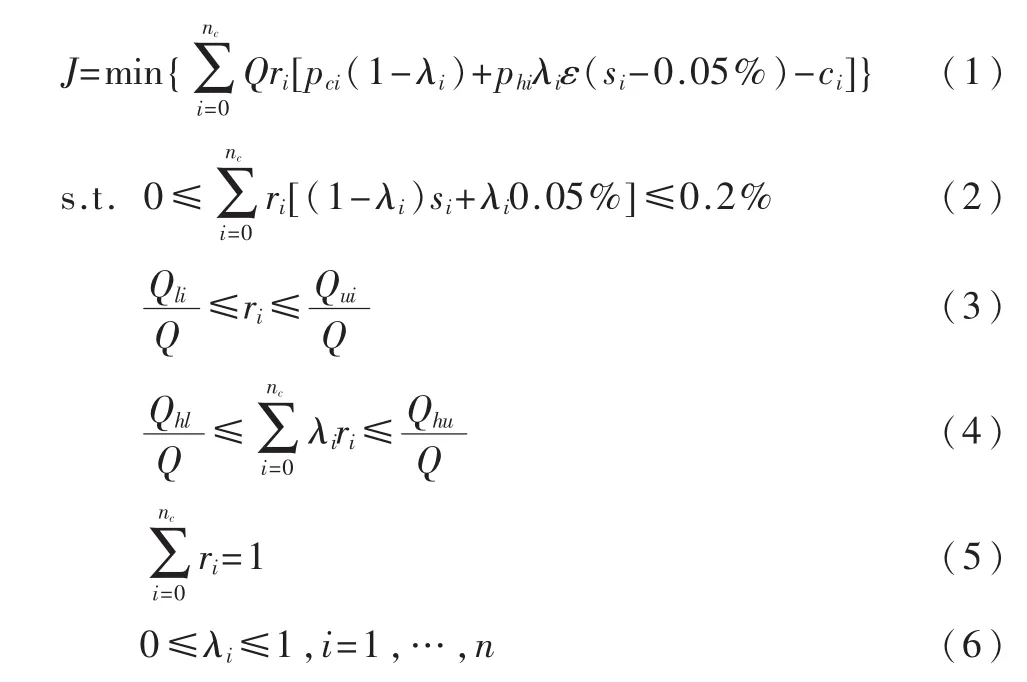
约束条件中，式（2）限制出厂柴油含硫率不得超过0.2%，式（3）将调合柴油第 i组分流量限制在该组分流量的上下限 Qui和 Qli之间，式（4）将加氢精制柴油总流量限制在加氢精制能力的上下限Qhu和Qhl之间。式（1）～式（6）表明，加工和库存成本优化即为在约束条件下，通过求解调合柴油各组分比例ri和组分中加氢精制的比例λi，使 J取最小值。

2 粒子群优化算法简述

粒子群优化算法是一种群体智能SI（Swarm Intelligence）算法，它结合了动物的群体行为特性以及人类社会的认知特性[5]。在该算法中，每个个体被视为在n维搜索空间中的一个不同的粒子，都具有速度和位置；速度决定了其运动的方向和速率，位置则体现了粒子所代表的解在解空间的位置，为评估该解质量的基础。算法要求粒子在进化过程中维护这两个向量。位置的维护，体现在每个粒子各自维护一个自身的历史最优位置向量，群体维护一个全局最优位置向量。假设在一个D维的搜索空间中，有m个粒子组成一个群体。其中第i个粒子在 D 维的搜索空间中的位置 xi=（xi1，xi2，…，xiD），i=1，2，…，m。将 xi代入目标函数可计算出其适应值，根据此值的大小衡量xi的优劣；对于最小化问题，目标函数值越小，对应的适应值越好。第i个粒子的历史最优位置记为 pi=（pi1，pi2， …，piD）， 群体最优位置向量记为pg=（pg1，pg2，…，pgD）。 速度则是由个体的飞行经验和群体的飞行经验进行动态调整；第i个粒子的速度vi=（vi1，vi2，…，viD），其第 d维的速度和位置按如下方程进行迭代更新：

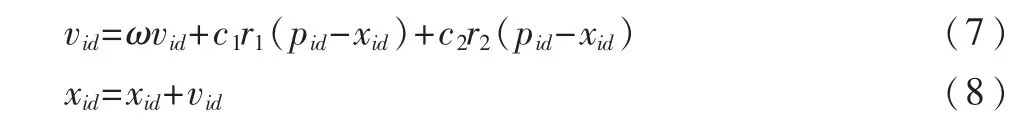
其中，ω为惯性权重，c1和 c2称为加速系数 （或学习因子），r1和 r2为[0，1]区间上的随机数。 由式（1）可见，ω用来控制粒子以前速度对现在速度的影响，其值较大时对全局搜索有利，较小时则对局部搜索有利；c1调节粒子飞向自身最优位置方向的步长，c2调节粒子飞向全局最优位置方向的步长。在更新过程中，算法要求粒子的速度在一个由用户设定的最大速度vmax的范围内。式（2）中的位置在每次更新后均要检查是否在搜索空间中，否则须进行修正。

粒子群优化算法的流程图如图1所示。

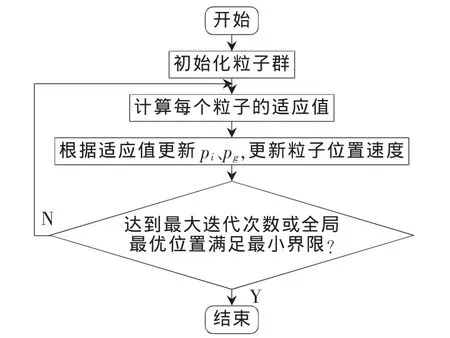
图1 粒子群优化算法的流程图

3 改进的粒子群优化算法

粒子群优化算法虽然容易实现、应用广泛，但也存在着早熟收敛、收敛精度不高的缺点，在求解多极值优化问题时难以获得真实的全局最优解。自该算法提出以来，研究者就不断地通过将其与其他搜索算法或者思想技术相结合来进行算法的改进。混沌优化算法作为一种较新的搜索算法，其基本思想是把变量从混沌空间变换到解空间，利用混沌变量在一定范围内具有随机性、遍历性和规律性的特点进行优化搜索，能使算法跳出局部最优，保持群体的多样性，具有全局渐进收敛和收敛速度快的搜索性能。本文尝试将这两种算法相结合，即使用一种新的混沌粒子群优化算法，将混沌融入到粒子的运动过程中，为粒子提供遍历参考点，增强其主动搜索性，以达到更好的效果。

算法步骤如下：

步骤（1）：初始化。设定种群大小m、搜索空间维数D、最大迭代次数为T，对粒子群和资源系数进行初始化。 其中，资源系数 a（d）=0.39+0.1×rand，rand 为区间上的均匀分布随机函数。

步骤（2）：定义 Logistic 混沌序列 c（t，d）。 即 c（1，d），rand，c（t+1，d）=a（d）×c（t，d）×（1-c（t，d）），t=1，2，…，T+4×D，d=1，2，…，D。 定义遍历参考点序列 x（t，d）=l （d）×c （T+4×D，d）， 其中搜索空间长度 l=（l（1），l（2），…，l（D））。定义 t时刻的随机动态邻域：ε（x（t），r）={p|p（d）∈[x（t，d）-r（d），x（t，d）+r（d），d=1，2，…，D]}，其中 r=（r（1），r（2），…，r（D））为指定随机动态邻域半径向量，r（d）=l（d）/（2×10round（5×rand）），round 为 取整 函数 。 设计一个与时间t相关的主动探测概率 p（t）=0.1+0.9（T-t）/T。

步骤（3）：更新全局最优粒子。 计算 p（t），若 rand＜p（t），则计算遍历参考点 x（t，d）和随机动态邻域半径向量 ε（x（t），r），并以采样率 m/10 对 ε（x（t），r）进行随机采样，选出m/10个点，通过比较确定个体最优粒子pi与全局最有粒子 pg；否则，令 pg=pi，转步骤（4）。

步骤（4）：若满足终止条件或 t＞T，则转步骤（5）；否则，转步骤（3）。

步骤（5）：输出最优解 pbestg（t），运行终止。

4 改进的粒子群算法在柴油排产中的应用

算法采用Java语言编程实现，开发工具为Eclipse IDE forJava Developers （Version：Juno Service Release 2），运行环境为 Java（TM）SE Runtime Environment（build 1.7.0_11-b21）。测试以某炼油厂一个月的柴油生产数据为例[6]，25种不同源地（种类）的原油经过蒸馏、焦化、催化等装置处理所生成的8种柴油将参与加氢精制与调合。将这些原油按其所生成的柴油的硫含量从高到低加以排序并用编号表示。粒子维数设为组分油的个数25，各粒子的初始位置和速度通过随机函数生成（定义随机函数时以使粒子的初始位置为各组分油的量附近的随机值、速度参数生成值稍小为宜），设定粒子群规模为80，最大迭代次数为10 000。算法运行20次，所得最优解可使编号前12种组分油进行加氢，所有组分油经调合后平均硫含量为0.194%，相比参考文献[6]的预测排产方案（编号前11种组分油进行加氢，所有组分油经调合后平均硫含量为0.191%）要稍优，并使库存成本处于较低的水平。具体数据见表1。

本文针对柴油生产过程中的加氢精制与调合优化问题，建立了加工和库存成本优化模型，并采用改进粒子群算法进行实验。测试所得最佳结果可使产品质量更加逼近临界合格标准从而降低柴油生产成本，同时也降低库存成本，对柴油排产具有一定的指导作用。此算法对于更多的组分油以及更多的质量指标的排产也具有一定的参考价值。

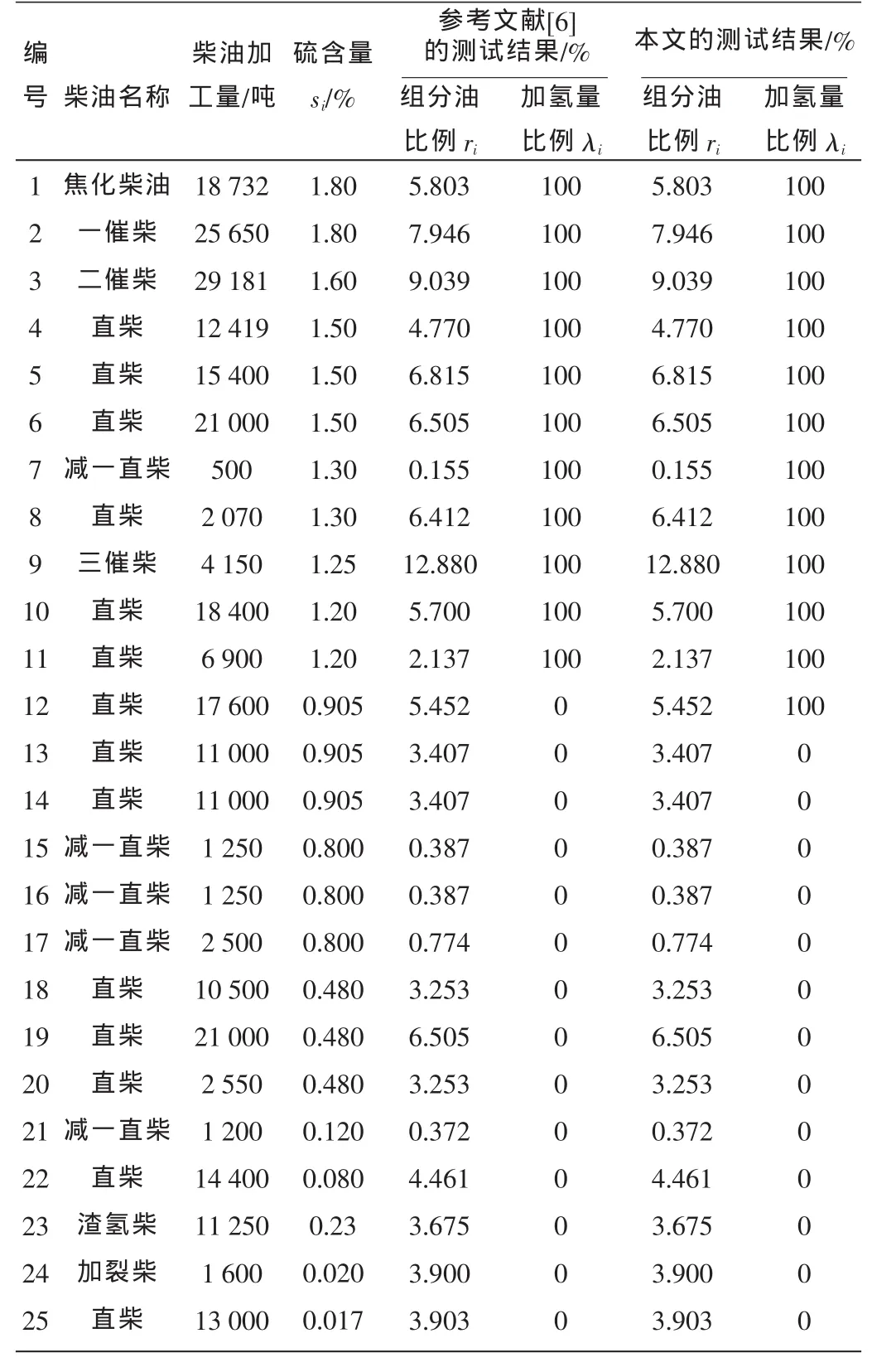
表1 柴油生产数据及测试结果

[1]蔡智，黄维秋，李伟民，等.油品调合技术[M].北京：中国石化出版社，2005.

[2]宁建华，赵英凯，李丽娟.基于改进粒子群算法的柴油调合配方优化 [J].化工自动化及仪表，2010，37（10）：22-25.

[3]黄平.粒子群算法改进及其在电力系统的应用 [D].广州：华南理工大学，2012.

[4]徐文星．混沌粒子群优化算法及应用研究[D]．北京：北京化工大学，2012.

[5]张军，詹志辉.计算智能[M].北京：清华大学出版社，2009.

[6]陈晓龙，吴世逵，梁朝林.柴油加氢精制工艺的线性规划优化[J].茂名学院学报，2003，13（4）：18-22.