基于改进共生矩阵BGLCM的半色调图像分类*

林海龙，文志强，周 济

（湖南工业大学 计算机与通信学院，湖南 株洲 412000）

许多的图像渲染技术只有二进制输出，例如：印刷领域、压缩存储、纺织及医学、数字打印设备等。将一幅0～255连续的图像通过一定的技术将其转换成 0、1的二值图像过程称为图像的半色调。图像的半色调是通过一个二值设备装置产生出一种连续图像的错觉方法，是使用黑白两点的密度表示图像像素值。有效的数字半色调可以大幅提高以最小的成本渲染图像质量，常用的半色调图像技术主要分为有序抖动、误差分散、点分散。通过误差分散法实现的半色调图像质量最好但算法复杂度相对最高，点分散法次之，有序抖动法最差但算法复杂度也最低。

在纸质图像的数字化、数字出版社系统、半色调图像的锐化、较色、压缩等图像的再处理领域需要将半色调图像转换成连续色调图像为图像的逆半调过程。逆半调技术在20世纪90年代有了一定的研究成果，当前公开报道过逆半调技术主要有滤波法、最优化估计法、机器学习法、矢量法等。大部分的逆半调方法均需要知道产生半色调图像的方法，例如参考文献[1]采用多尺度梯度估计法以及参考文献[2]采用MAP最大后验概率估计的逆半调就需要知道误差分散的分散核，针对误差分散抖动掩膜技术[3]就需要知道相应的半色调图像抖动方法，所以半色调图像的分类研究便显得十分必要。灰度共生矩阵（GLCM）常用灰度图像的特征提取，具有较好的效果。本文在传统共生矩阵的基础上对其进行改进提出适应于二值图像特征提取的BGLCM。

1 半色调图像分类回顾

在公开发表的刊物中对半色调图像分类研究的文献相对较少，最早的为Chang Pao-Chi[4]在1997年提出了LMS滤波的半色调图像复原即逆半调过程，为了设计不同种类滤波模板参数，使用了一维自相关函数提取出半色调图像特征，且用该数据训练神经网络，而后支持按半调类型初始化不同尺度的滤波模板，且依据LMS原理迭代生成相应类型的滤波模板系数。但文中仅仅对clustered-dot、constrained average、dispersed-dot、error diffusion 4类半色调图像进行了分类，显然当前的半色调技术不止上述的3种，当error diffusion的误差分散核就存在6种，而Bayesian算法在应用中就需要知道误差分散核的种类。

孔月萍[5]等人在Chang Pao-Chi的一维自相关函数基础上提出了半色调图像自相关与纹理特征相结合的半色调图像分类算法，文中将半色调图像通过适当的分辨率进行按照式（1）“下采样”将得到M/2×N/2（M、N为原图像尺寸）的0～7级灰度级图像。之后提取出共生矩阵（GLCM）、灰度游程矩阵（GLRM）的纹理逆差距特征C和线纹理特征R，之后结合自相关函数提取特征通过最邻近分类器进行分类。实验结果表明相对于参考文献[4]分类的种类及准确率明显提高，但文中仅将半色调图像分成ED和有序抖动两大类。半色调图像类别除了ED和有序抖动两大类还有块置换法、模板替换像素法、meseDotDitherHvs、meseDotDitherWeighting等，且半色调图像自相关与纹理特征相结合的半色调图像分类算法时间复杂度高，会大大的降低特征提取效率。

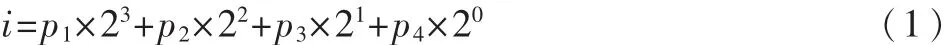
2 灰度共生矩阵及其特征

图像的纹理是图像给人传达最直接的线索，图像的特征通常包括颜色、形状及纹理，纹理即是图像像素值与其像素值的空间分布，是图像中普遍存在且又难以描述的特征。纹理特征提取主要是将图像中像素值、空间分布关系用一定的数学模型计算出特征值。其提取标准主要有维数少、可靠性好、识别能力强、提取过程的时间复杂度低等。

关于纹理特征提取算法主要追溯于20世纪70年代，参考文献[6]将纹理特征的提取分为统计类、模型类、信号处理类、结构类4种。本文将灰度共生矩阵GLCM（G rey Level Co-cocurrence Matrix）作一个简要的描述，G LCM首先由Julesz[7]提出之后由Haralick[8]证明其用于特征提取中具有较好的有效性。但由于待提取的半色调图像是一个只含有0、1的二值图像，传统的共生矩阵便失去了统计意义所以提出基于共生矩阵思想上的改进算法。

f为一幅连续的灰度图像，其灰度值为0～L。G为一矩阵，该矩阵的元素gij是f图像灰度值i、j在位置相对算子Q（为d、φ函数）出现次数，其中，0≤i，j≤L。按照该种方法形成的矩阵G称之为灰度共生矩阵，其求解过程如图1所示。

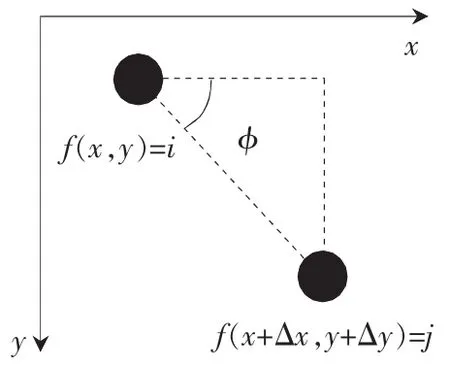
图1 共生矩阵求解图

共生矩阵G的大小和原连续图像f的灰度值L有关，在实际的运用中为了计算上的方便常将灰度值L划分成n等分，将0～L灰度值量化成0～n从而缩小G的大小，减少计算过程中的时间复杂度。同时使用式（2）共生矩阵出现的概率来替代其次数大小。

在对原始连续的图像提取共生矩阵时，为了能更好地描述原图像纹理特征，参考文献[9]计算出了共生矩阵G的8种描绘子，式中省略参数d、φ。

（1）最大概率

度量共生矩阵G的最强响应，其值越大表明该店响应最大，值域为[0，1]。

（2）相关性

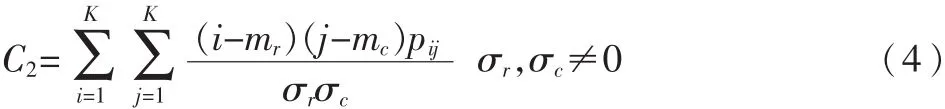
度量一个像素与其邻域像素的相关性，值域为[-1，1]，若任意的一个标准差为0，则像素的相关性无意义。

（3）对比度

纹理对比度是表示GLCM的一个像素与其邻域其他像素灰度对比的度量，反应了图像纹理的清晰度。

（4）熵

反应了GLCM图像像素的随机性以及信息量的多少，由公式可知当所有的pij为零时熵值为 0，当pij值相等时熵值最大。

（5）同质性

反应了GLCM矩阵对角线元素空间分布的紧密度，当其元素全部位于对角线时值最大，其值的范围为[0，1]。

（6）一致性

GLCM的一致性为G矩阵各个元素平方之和，其值域为[0，1]，它反映了灰度分布均匀程度和纹理粒度。

（7）逆差距

灰度共生矩阵GLCM的逆差距反应了图像的均匀性，其值越大则图像越均匀。

（8）角二阶矩

3 算法设计

产生半色调图像主要分为误差分散（Error diffusion）、点分散（Dot diffusion）、有序抖动法（Ordered dither）、直接二值搜索法（Direct binary search）。通过参考文献[9]可知有序抖动与点分散法时间复杂度低，但半色调图像的质量较差，误差分散法时间复杂度低，质量好，直接二值搜索法时间复杂度最高但产生的半色调图像质量最好。

在实际应用与研究中虽然直接二值搜索法[10]能够产生最好的半色调图像，但由于其时间复杂度很高，所以并非常用。误差分散法使用最多，其次为点分散法，最后为有序抖动法。误差分散法和点分散法主要用于人物、景观等打印显示，有序抖动法主要用于图形类图像。

图2为常见的半色调图像，设计算法对其特征进行提取，将提取之后的特征通过BP神经网络分类，实验结果证明该算法在半色调图像分类准确率且分类种类均优于传统GLCM，适用于二值图像的特征提取及分类，故将其称为BGLCM。

图2 待分类半色调图像

由于半色调图像是一个二值图像，所以将其转换成灰度共生矩阵（GLCM）得到的是一个2×2的矩阵如图3所示，元素为在位置相对算子Q上在原图同时出现（0，0）、（0，1）、（1，0）、（1，1）的次数，那么该共生矩阵便失去了统计意义。本小节就在基于灰度共生矩阵的思想上将其进行改进使其适用二值图像的特征提取。

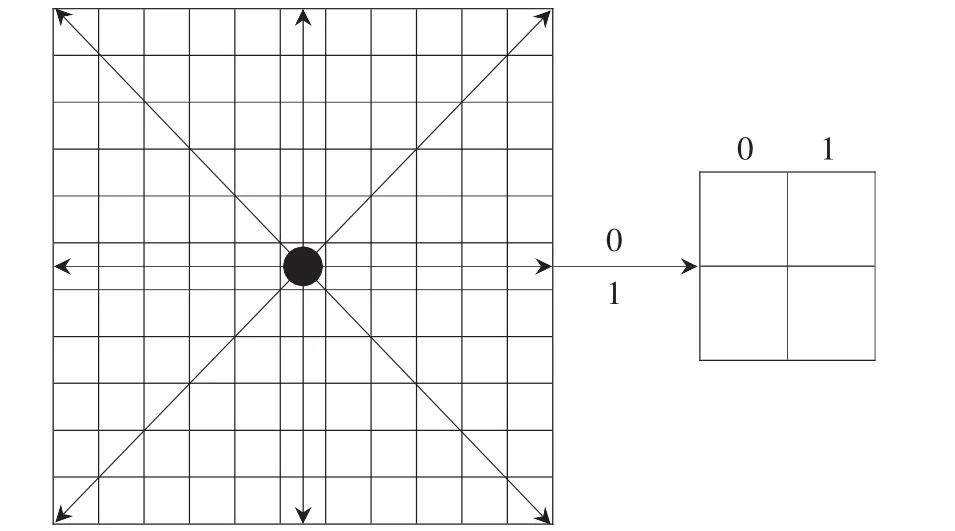
图3 半色调图像对应的GLCM

半色调图像产生的 GLCM 其元素值g（i，j，d，φ）（i，j=0或 1，d、φ由Q确定）如图 1所示，通过不断地改变位置相对算子Q便会产生不同的GLCM，每个相对算子Q在（0，0），（0，1），（1，0），（1，1）均会有一个统计值与之相对应。 通过实验证明仅当（0，1）或（1，0）时的统计值对分类是有效的。 文中将d取 1～5，φ 值取 0°，45°，90°，135°，180°，225°，270°，315°的 8 个 方 向 如 图 3 所 示 ，那么每幅半色调图像就会产生40个共生矩阵G，将每个矩阵对应（0，1）、（1，0）的统计值相加作为该共生矩阵G的一个特征值，总共有40个共生矩阵那么就存在40个特征值作为一幅图像的特征向量B。之后将统计的特征数据通过式（9）最大最小规格化方法将其归一化。

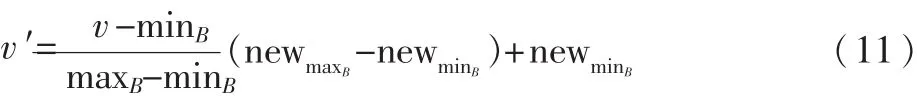
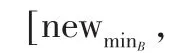
4 实验结果分析

本实验在Windows XP操作系统环境下进行操作，采用VC6.0结合OpenCv及Matlab进行编程。通过对12种半调方法产生的半色调图像库中每一类随机地取出2 000幅图片通过上述传统共生矩阵（GLCM）及改进之后共生矩阵（BGLCM）算法的特征进行提取及归一化，之后从2 000个特征向量中随机抽取10个特征向量形成特征曲线比较如图4所示，由上至下依次对应着图2所示的半色调图像类型。

图4显示了使用传统共生矩阵（GLCM）和改进之后共生矩阵（BGLCM）对半色调图像特征提取形成特征曲线图，横轴代表每幅半色调图像的特征数8和40，纵轴为每一个特征数对应的特征值，由图中可见两种算法产生的半色调图像的特征曲线均具有很好的拟合度，但传统的共生矩阵（GLCM）产生曲线图在不同种类之间识别度不高而改进之后共生矩阵（BGLCM）不同类型的曲线又有很好的辨识度适合分类。

从产生的特征向量中选取500个特征对BP神经网络进行训练，之后随机选取1 500个特征向量经过训练之后的BP神经网络进行测试得其分类的准确率如表1、表 2 所示，表为一 个矩 阵 A（i，j）（1≤i≤12，1≤j≤12），其中i，j分别对应着图 2中的 12类半色调图像，A（i，i）（1≤i≤12）即对角线上数目为第i类正确数目，第13列为各类分类准确率。表中反应出在同一个实验环境由传统的灰度共生矩阵对12类半色调图像提取的特征通过BP神经网络进行分类的准确率较改进之后的BGLCM更差。

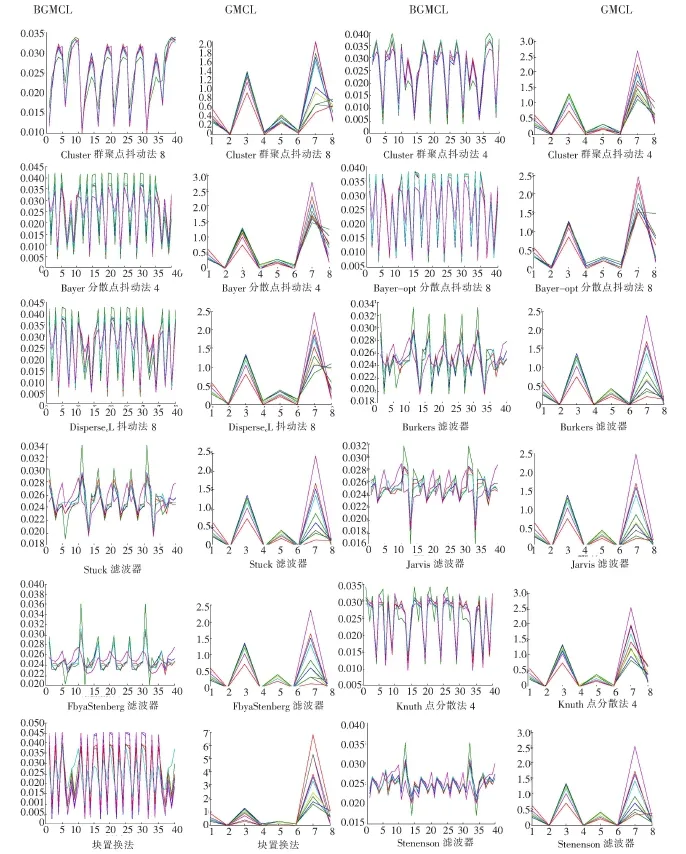
图4 特征图差异比较

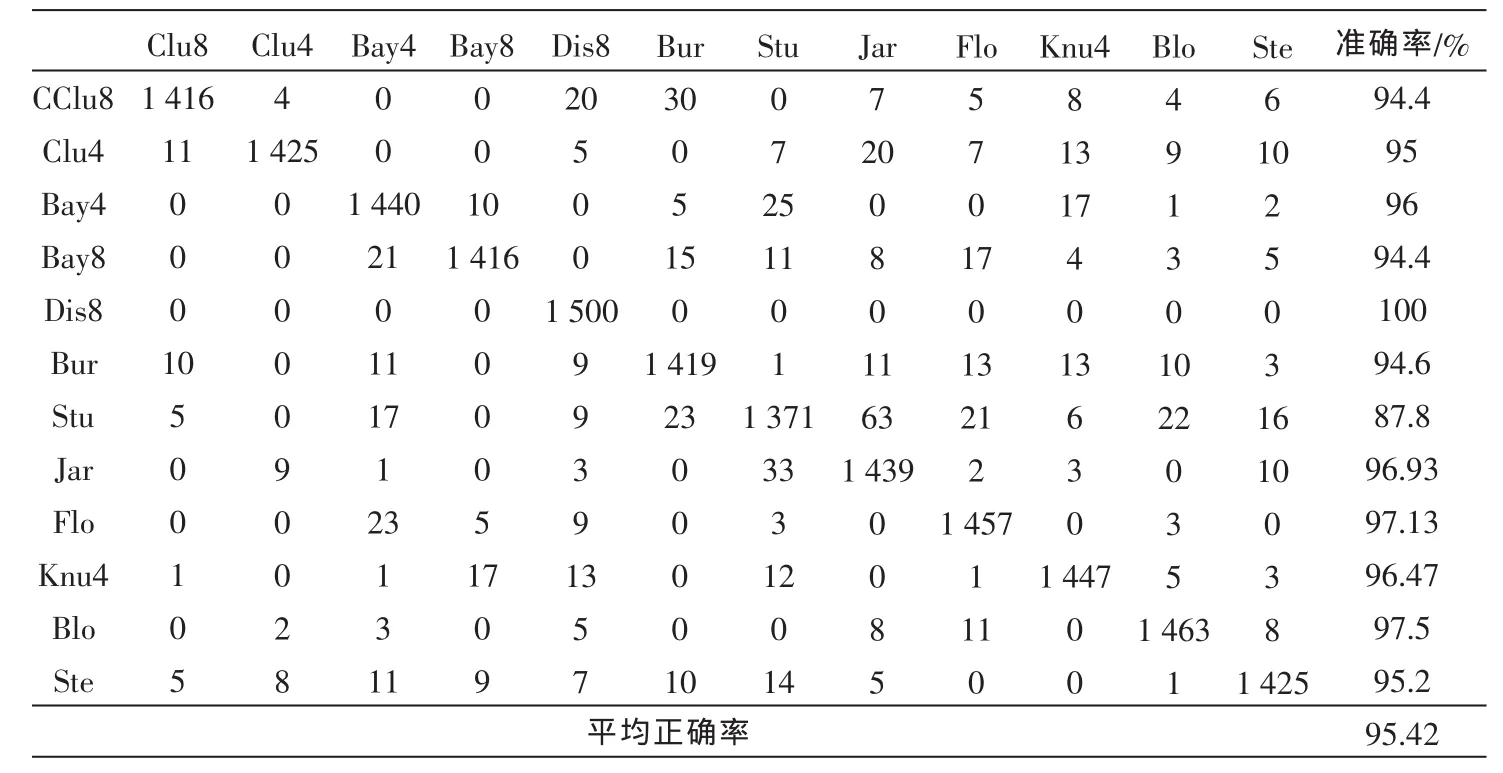
表1 改进BGLCM分类准确率

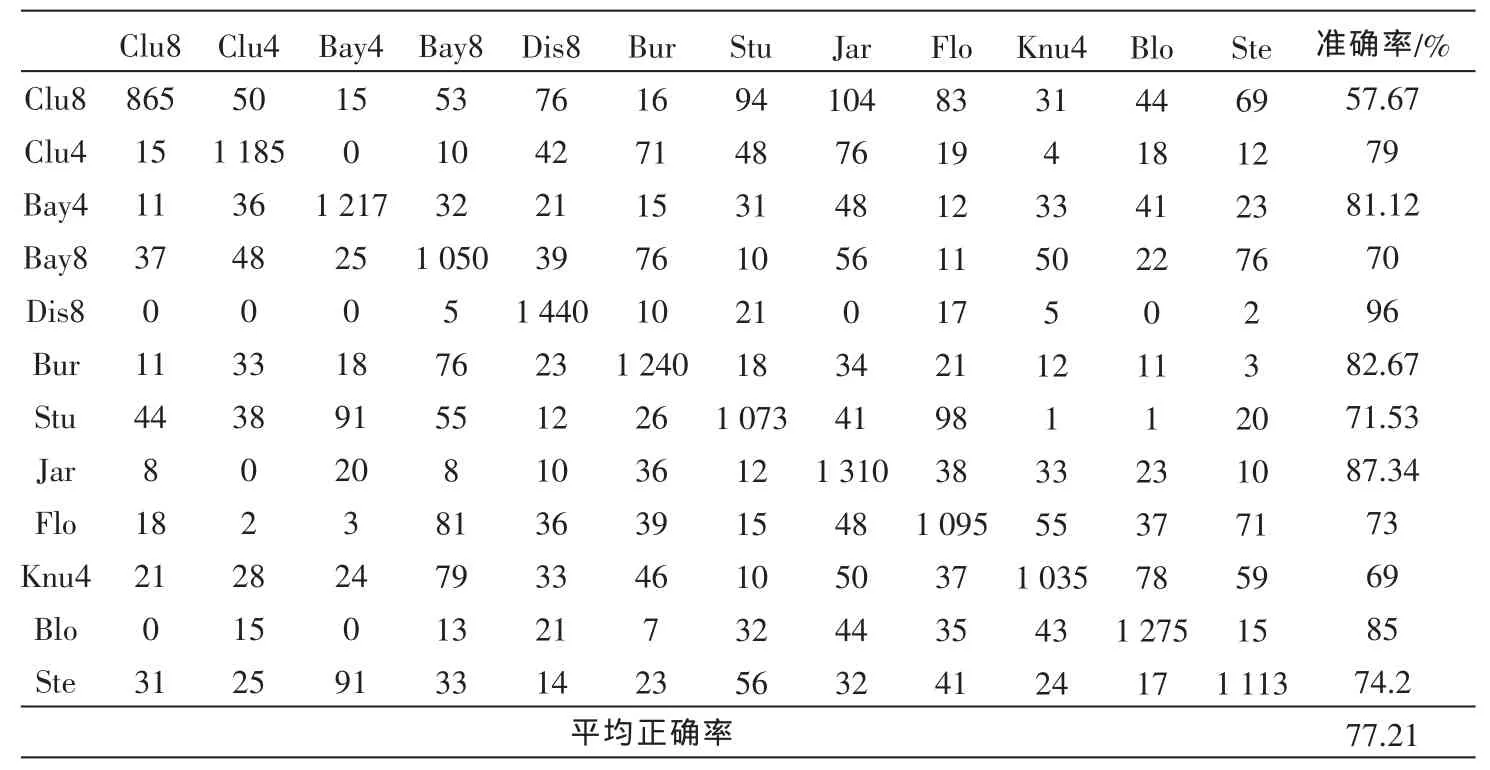
表2 传统GLCM分类准确率

本文先介绍了半色调技术的应用与常用的一些技术以及半色调图像的再重建需要将二值图像通过逆半调技术将其转换成连续色调的灰度图像。在逆半调技术中大部分需要知道相应半色调图像产生的方法，所以对半色调图像的分类就显得十分重要。之后分析现有的半色调图像分类相关报道的不足之处，同时基于传统的共生矩阵（GLCM）思想上对其进行相应的改进使其适用二值图像分类的BGLCM，改进之后的BGLCM省略了求共生矩阵的特征值而是对不同的相对算子 Q含有（0，1）和（1，0）元素进行统计，相对传统共生矩阵可以减少算法的时间复杂度，通过实验分析可以看出在同一个实验环境中经过改进之后的BGLCM对二值图像分类准确率优于传统的灰度共生矩阵。

[1]KITE T D， DAMERA-VENKATA N， EVANS B L， et al.A fast high-quality inverse halftoning algorithm for error diffused halftones[J].Image Processing，IEEE Transactions on， 2000， 9（9）： 1583-1592.

[2]STEVENSON R L.Inverse halftoning via MAP estimation[J].Image Processing， IEEE Transactions on， 1997， 6 （4）：574-583.

[3]KARNIZ， FREEDMAN D， SHAKED D.Fastinverse halftoning[C].31st International Congress on Imaging Science（ICIS 2010）， Beijing， China.2010.

[4]CHANG P C，YU C S.Neural net classification and LMS reconstruction to halftone images[C].Photonics West′98 Electronic Imaging.International Society forOptics and Photonics，1998：592-602.

[5]孔月萍，杜旭苗.一种半调图像类型识别方法[J].计算机应究，2009，26（12）：4850-4851.

[6]刘丽，匡纲要.图像纹理特征提取方法综述[J].中国图象图形学报，2009，14（4）：622-635

[7] JULESZ B. Visual pattern discrimination[J].InformationTheory，IRE Transactions on， 1962， 8（2）： 84-92.

[8]HARALICKRM，SHANMUGAM K， DINSTEIN I H. Textural features for image classification[J].Systems， Man and Cybernetics，IEEE Transactions on， 1973 （6）：610-621.

[9]孔月萍，曾平.图像逆半调及其质量评价技术研究[D].西安：西安电子科技大学，2008.

[10]ANALOUIM，ALLEBACH JP.Model-based halftoning using direct binary search[C].SPIE/IS&T 1992 Symposium on Electronic Imaging： Science and Technology.International Society for Optics and Photonics， 1992： 96-108.