由单桩静载试验曲线推求群桩沉降研究

□文 /董光辉

由于桩基工程施工条件的复杂性和理论计算方法的局限性使得群桩沉降计算结果与实际结果相差较大，所采用的经验修正系数变化范围也太大，以至于群桩沉降计算始终是个难点，因此正确预测群桩沉降显得越来越重要。

实际上，群桩基础沉降与桩基实际特性、施工方法和实际土层状况等密切相关，而单桩试桩曲线包含了丰富的桩土相互作用信息，在一定程度上直接反应了现场土质的力学性且包含了桩土相互作用信息，但目前单桩试验曲线一般只应用于验证单桩承载力设计值，很少直接用于群桩沉降计算中。本文以单桩静载荷试验结果为基础，预测群桩沉降；对比分析表明该方法切实可行，具有较强的适用性。

1 桩基沉降设计和研究中的问题

1.1 桩基沉降计算方法存在的问题

目前国内常用的方法有实体深基础法和基于Mindl in解法的弹性理论法[1]。实体深基础法计算桩基础沉降是在工程实践中最广泛应用的近似方法。该方法假定桩基如同天然地基上的实体深基一样工作，认为桩与桩间的地基土形成一实心体，其深度可取不大于桩长的某一比例，地基土与连接桩的基础形成混合刚体而一起下沉，因此沉降就等于实心体以下地基土的压缩变形；其沉降计算沿用浅基础的沉降计算方法。该方法是桩基沉降计算的最简单模式之一，但它忽视了影响桩基沉降的桩距、桩长、桩数及排列形式等对沉降的影响。基于Mindl in解法的弹性理论法则认为桩与土是两种地基介质，考虑两者的相互作用，建筑物沉降就等于桩土的垂直变形，能够计算群桩中各桩的沉降和差异沉降。弹性理论法能考虑群桩中桩-桩、桩土相互作用特性，从而能够考虑桩数、桩位布置、桩径、桩长对沉降的影响，比较符合实际。Poul os[2]通过大量的计算机运算，提供了许多参数曲线与表格。这些图表使得在工程设计中应用弹性理论分析桩基沉降及其他性状成为一种得以实施的较为完整的体系,但由Cooke[3]的试验结果得知，弹性理论解过高地估计了群桩相互作用。因此，该方法很难准确确定群桩沉降。

1.2 桩基沉降设计方法存在的问题

在桩基础设计中，一般都要进行单桩的静载荷试验。单桩静载荷试验得出的试桩曲线一般只应用于验证单桩承载力设计值，实际上单桩静载荷试验得出的载荷位移曲线包含了丰富的桩土相互作用信息，不仅反映了土体分层、土体性质，还反映了桩本身质量以及弹性和塑性变形等。因此单桩试验没有得到充分的重视，使得很多有用的资料被弃之不用。因此，如何利用单桩静载荷得出的载荷位移曲线推求群桩沉降是值得研究的问题。

2 利用单桩静载试验推求群桩沉降

利用单桩载荷试验的载荷位移曲线和群桩沉降比推求群桩沉降，将单桩静载荷试验这一很有价值的曲线应用到群桩变形设计计算中，使桩基设计更加合理。

2.1 由单桩试验推求群桩沉降的研究进展

几十年来，国内外研究人员对此做了大量的工作。首先由Skempt on[4]提出沉降比概念并建立了砂土中群桩沉降与单桩沉降之比的纯经验关系式，Meyer hof[5]和Vesic[6]也各自提出了经验公式，这些经验公式在一定程度上应用了单桩试桩曲线，但是该方法缺乏理论指导。自从Poul os[7]提出相互作用系数以后，许多学者采用此概念对沉降比进行了改进。Randol ph&Poul os[8]提出了一个相当实用的近似公式用以预估Gibson土的群桩沉降比；杨敏[9]对Gibson土中群桩也提出了群桩沉降比折减系数并给出了图表；另外由于桩邻近的土模量可能比桩之间土体的模量小很多[10]，Poul os提出了考虑土模量径向变化的分析方法；Hewitt对于不相似的桩之间的相互作用给出了近似方法[11]；Chow[12]提出了采用Muki理论考虑桩的加筋效应。Randol ph&Wr ot h[13]认为桩基础的塑性部分的变形对其他桩影响很小，从而提出了在群桩变形计算中只考虑弹性变形叠加对群桩的影响，单桩中的塑性变形对群桩中其他桩不产生沉降影响。Mandol in&Viggiani[14]对此也进行了相似的研究。

虽然Randol ph认为单桩中的塑性变形对群桩中其他桩不产生沉降影响，但整理苏联学者1939年的试验结果[15]发现不同群桩中的塑性变形并不相同。

从图1和图2知：在某一载荷下随着桩数的增大，塑性变形也在增大，而且随着载荷水平的增大塑性变形也在增大。

图1 单群桩载荷沉降曲线

图2 不同桩数情况下的塑性变形大小

2.2 基于静载试验的群桩沉降分析法

在实际工程中，单桩的载荷位移曲线中某一载荷对应的位移包含了2部分，一部分是桩土之间的弹性变形，一部分是不可恢复的塑性变形，见图3。

由图3可知，一般都存在卸载回弹曲线，当试验的载荷较大时，则不可恢复的变形就较大，但不同载荷的回弹曲线斜率都比较接近，因此可以从原点画一条平行于卸荷回弹曲线来划分它们。如果没有卸荷回弹曲线，则可简化地从零点做一切线来划分弹性变形和塑性变形。

因此某一载荷下单桩沉降可以分成下式

式中：S为某一载荷对应下的单桩位移；Se为位移的弹性变形部分；Sp为位移的塑性变形部分。

由于塑性变形不能叠加，本文在此基础上提出了弹性沉降比和塑性沉降比，即

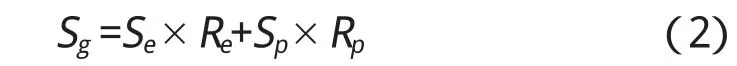
式中：Sg为群桩沉降；Se为单桩的弹性沉降；Sp为单桩的塑性沉降；Re为弹性沉降比；Rp为塑性沉降比。

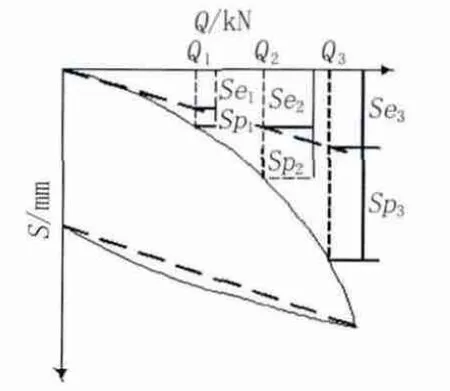
图3 单桩试桩曲线

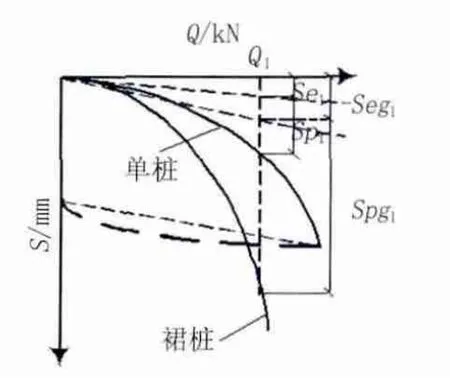
图4 单桩和群桩的载荷沉降曲线

3 弹性沉降比和塑性沉降比的确定

Poul os在考虑桩与桩之间的相互影响时，仅对两桩变形简单叠加[2]，而未考虑桩的存在对地基土变形所带来的影响，忽略了桩群在土中的加筋效应。

Muki（1970）基于量纲分析基础上，采用较为严密的轴向受荷弹性杆件在无限体半空间中理论解，提出能够考虑桩体存在影响的桩-桩相互作用系数分析方法[16]。

由n根桩组成的群桩基础，桩桩相互作用系数计算至少涉及2根桩之间相互作用。首先以2根桩为基础计算相互作用系数。在弹性半空间中建立三维坐标体系{0，x，y，z}以第 i、j桩为研究对象，求解相互作用系数。然后再推广到3根以上桩的相互作用系数。其中桩i直径为di，截面面积为Api，桩长为li，弹性模量为Epi；桩 j的直径为 dj，截面面积为 Apj，桩长为 lj，弹性模量为Epj；桩间距为Sij；半空间地基土的弹性模量为Es和 νs。

根据Muki&St er nber g的方法将真实桩分解为虚拟土和虚拟桩。由虚拟桩与虚拟半空间土在桩身的竖向应变协调来求群桩沉降，从而可以求出相互作用系数。根据上述理论得出了4×4和5×5群桩的Re值,然后根据Poul os[2]从应用的角度上考虑，对于较多桩数的群桩（n＞25），其Re值可近似按下式计算

为估计塑性沉降比的大小，本文提出以下计算公式

从上式可以看出，在某一载荷水平下，当弹性沉降越大，则塑性沉降比越小；同理弹性沉降越小，塑性沉降比则越大。从图4可见，随着载荷水平的增大，塑性沉降增加的速率比弹性沉降增加速率大，由式（4）得出塑性沉降比变小，从而保证群桩沉降预测较合理。

4 实例分析

某学院18层教工住宅楼[17]系框架-剪力墙结构，建筑高度为56.15 m，基础平面为23.8 m×32.2 m,总桩数为152根，桩长为32～33 m，桩径为0.6、1 m两种，基础布置和基础土的性质见图5和表1。

图5 基础平面布置图与单桩试桩曲线

表1 各土层的物理力学性质指标

桩长取 32.5 m，桩径为 0.8 m，l/d=40.6，s/d=4,直径为0.6 m的单桩设计载荷为1.6 MN，直径为1 m的单桩设计载荷为2.8 MN，因此取桩的设计载荷为2.5 MN。由于土的扰动，土的弹性模量的取值较困难，因此很多学者提出了相应的经验公式[2]。本文综合单桩试验曲线取Ep/Es=1 500。根据前面求弹性沉降比的方法可以得出R16=5.628，R25=7.557，根据式(3)可以得出Re=21.69。从图4知在单桩载荷为2.5 MN，单桩沉降为1.5mm，根据前面的方法可以得出弹性沉降为1.0mm，塑性沉降为0.5mm。得Rp=5.42。则由式(2)知：Sg=21.69×1+5.42×0.5=24.4(mm),实测沉降为25mm。本文得出的沉降部分考虑了工后沉降，如果要计算长期沉降则需要在此基础上进行修正。

5 结论

1）单桩静载荷试验得出的载荷位移曲线包含了桩土相互作用信息，不仅反映了土体分层、土体性质，还反映了桩本身质量、弹性和塑性变形等。本文采用试桩曲线法推求群桩沉降，充分利用了单桩静载荷试验曲线，使桩基设计更加合理。

2）提出了弹性沉降比和塑性沉降比并给出了弹性沉降比和塑性沉降比的计算公式，同时指出塑性沉降比随着载荷水平的变化而变化。

3）根据本文提出的群桩分析方法，对某学院18层教工住宅楼工程实例分析得知，其计算结果和实测结果较接近，证明了本文方法合理可行。

[1]桩基工程手册编写委员会.桩基工程手册[M].北京：中国建筑工业出版社，1995.

[2]Poul os.H.G.&Davis,E.H.Pi l e f oundation anal ysis and design[M].John Wi l ey and Sons,New Yor k,1980.

[3]Cooke,R,W.,Price,G&Tarr,K.Jacked pil es in London cl ay：int eract ion and group behaviour under working condit ions[J].Geot echnique,1980,30(2)：97-136.

[4]Skempt on,A.W.Discussion：Pi l es and pi l e f oundat ions,S-et t l ement of pi l e f oundation[C].Proc.3rd ICSMFE,Zur ich,1953,172-174.

[5]Meyer hof,G.G.Compact ion of sands and bear ing capacit y of pi l es[J],J.SMFD,ASCE,1959,85(SM6)：1-30.

[6]Vesic,A.S.Exper iment s wit h inst r umented pil e gr oups in sand[C].Per f ormance of deep f oundations,ASTM,STP 444，1969，177–222.

[7]Poul os,H.G.Anal ysis of the set l ement of pi l e Gr oups[J].Geotechnique 1968，18(4)：449-471.

[8]Randol ph,M.F.&Poul os,H.G.,Est imat ion of the f l exibil it y of of f shore pil e gr oups[C].Pr oc.2nd Int.Conf.Numer ical Method in Of f shor e Pil ing,Austin.1982.

[9]杨敏,上部结构与桩筏基础共同作用的理论与试验研究[D].同济大学,1989.

[10]O’Nei l l,M.W.,Ghazzal y,O.I.&Ha,H.B.Anal ysis of three dimensional pi l e gr oups with nonl inear soil response and pi l e-soil-pi l e int er act ion[C].Pr oc.9t h Annual Of f shor e Technol ogy Conf er ece,Houst on,Texas.1977.

[11]Poul os,H.G.Modi f ied cal cul ation of pil e group set t l ement inter action[J].J.Geot ech.Engng,ASCE,1988.Vol.114,Vol.114,No.GT8.

[12]Chow,Y.K.Iterat ive anal ysis of pil e-soi l-pil e interaction[J].Geot echnique,1987,37(3):321-333.

[13]Randol ph,M.F.&Wroth,C.P.An anal ysis of t he vert ical def or mat ion of pil e gr oups[J].Geot echnique,1979,29(4):423-439.

[14]Mandol ini,A,&Viggiani,C.Sett l ement of pi l ed f oundations[J].Geot echnique 1997,791-816.

[15]陈惠康，桩基沉降分析[J].上海地质，1990，（1）：1-18.

[16]Muki,R.,Ster nber g.E,El ast ostat ic l oad-t ransf er to a hal f-space f rom a par tial l y embedded axial l y l oaded r od[J].Int er nat ional Jour nal of Sol ids and St ructures,1970,6(7):69-90.

[17]孙 毅.高层建筑独立承台桩基础的桩土共同作用分析研究[D].南京：东南大学,2003.