用改进的Duffing理论判断轴承故障的微弱信号

任学平，刘桐桐

（内蒙古科技大学机械工程学院，内蒙古包头014010）

用改进的Duffing理论判断轴承故障的微弱信号

任学平，刘桐桐

（内蒙古科技大学机械工程学院，内蒙古包头014010）

分析了传统Duffing振子混沌系统的基本理论对检测微弱信号的不足，给出了基于改进之后的Duffing振子检测微弱信号的新方法。改进后的方法能够突破传统方法对系统固有频率的限制，检测具有较大固有频率的微弱信号。通过一个实例，利用传统方法和改进方法分别对轴承外圈故障信号进行验证性分析，发现改进方法能更好的找出微弱故障信号。经过对仿真信号分析和轴承故障诊断实验，结果验证了检测方法的有效性。

振动与波；混沌理论；Duffing振子；改进算法；信号检测；轴承故障

轴承作为各种旋转机械中应用最广泛的一种通用机械零件，它们在旋转机械中起着十分重要的作用。经过初步的统计，在旋转机械故障损失中，因为轴承出现故障而造成的损失占到所有损失的1/3[1]。如何在轴承故障出现之初将其发掘出来，把故障发现在萌芽中，将会对社会产生巨大的经济效益。因此，提出一种能够有效判别轴承故障的方法势在必行。

在轴承工程实际应用过程中，轴承故障出现之初，发出的信号往往只是微弱的特征信号。在分析时发现，轴承的微弱信号包含着轴承本身极为丰富的运行信息，因此对微弱信号的检测分析现已成为检测轴承早期故障的最主要方法之一。但是这种微弱信号的幅值相对于噪声是微乎其微的，因此在实际问题分析过程中，发现微弱信号通常会被强噪声所淹没，很难将微弱信号识别出来。如何将淹没在强噪声中的微弱信号识别出来是现如今信号处理和故障诊断的重要研究内容[2]。

1 基于混沌振子检测信号的方法

1.1 传统Duffing振子方程

用小幅度的与内驱动力角频率相近的周期信号对传统Duffing方程的周期内驱动力进行摄动，并且考虑到谐波的影响，最终得到的Duffing振子方程如式1所示[3，4]

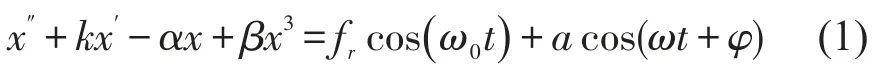
式中

frcos(ω0t)——周期策动力；

k——阻尼比；

ω0——内策力角频率；

-αx+βx3——非线性恢复力；

a cos(ωt+φ)——待测微弱信号。

采用4阶Runge-Kutta[5]对（1）式进行数值微分。令x′=y，则（1）式变为

Duffing振子方程对初值具有很强的敏感性，即给定系统一个固有频率ω0和周期策动力fr，当输入信号a cos(ωt+φ)后，系统的周期策动力发生改变。若在系统输入外界信号之前通过改变fr将系统调节至临界大尺度周期状态，输入外界信号后系统变为大尺度周期状态，则可以反映出存在和给定系统固有频率相近的一个微弱正弦信号。

经过大量的仿真实验表明，当ω0数值比较小时，系统能够很好的表现出大尺度周期状态，但是当ω0大于某一值后，发现系统总是在大尺度周期状态和混沌态之间变换。通过对传统Duffing方程不同内策力角频率ω0进行模拟仿真，发现当ω0＞13时即使加入微弱信号系统也不总能进入大尺度周期状态，很多时候会对是否存在故障信号进行误判。

令式（2）中k=0.5，fr=0.723 5，α=β=1，ω0=1，ω=1.01时，利用wolf方法对Duffing振子最大Lyapunov指数计算[6，7]，Duffing方程相图如图1所示：（a）为系统在没有加入待测信号时相轨迹图；（b）为系统在加入待测信号后的相轨迹图。通过比较可以很明显的看出系统在加入待测信号后进入尺度周期态，反映出待测信号中含有微弱同频周期信号。

令（2）中k=0.5，α=β=0.5，ω0=15，ω=15.03，得出系统临界阈值fr=0.764 9，系统加入微弱信号前后系统相图如图2所示：（a）为系统在没有加入待测信号时相图；（b）为系统在加入待测信号后的相轨迹图。通过仿真实验发现，加入微弱周期信号后系统仍然处于混沌状态。

1.2 改进Duffing振子方程

在轴承故障诊断实际应用过程中，轴承各部件的特征故障频率基本都在50～240 Hz之间，若采用传统的Duffing振子方程将无法对轴承故障进行准确的判断。为了提高轴承故障的准确判断率，需要对传统Duffing方程进行进一步改进。

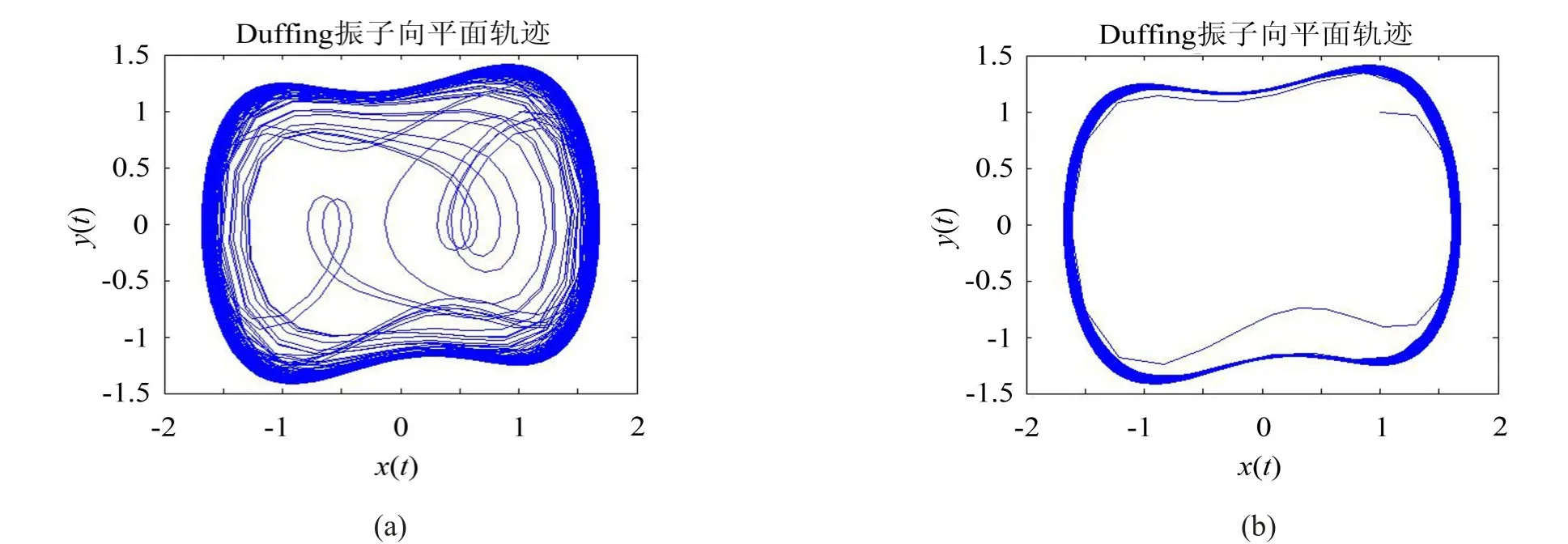
图1 w=1时系统相轨迹图

Duffing方程为非线性方程，方程主要由系统给定的非线性恢复力和随外界条件而变化的周期策动力两部分组成。通过进一步的研究发现，传统Duffing振子方程不能满足要求，主要是因为传统Duffing振子方程中非线性恢复力不能够满足非线性要求。因此需要对系统的非线性恢复力进行进一步的改进，目前比较常见的是将传统方程改为αx3-βx5[8，9]，现尝试将传统方程改为αx5-βx7，并且通过和传统方程进行比较，发现改进后的方程非线性性能有了显著提高，但随之而来计算量也随之增大。通过对同一套方程进行模拟，若采用αx3-βx5，需要18.10 s，而采用αx5-βx7，则需要18.62 s。改进后的Duffing振子方程为

为了验证改进后Duffing方程相比传统方程的优越性，利用改进Duffing方程对上述混有高斯白噪声的微弱周期信号进行模拟仿真。令（3）中k=0.5，α=β=1，ω0=ω=15，通过对改进Duffing方程进行最大lyapunov指数计算得出，系统临界阈值fr=0.826 69，得出系统加入微弱信号前后系统相图如图3所示。

图3表示改进Duffing方程的相轨迹图。其中(a)为没有加入待测信号时的相图，(b)表示加入待测信号后的相图。对图2和图3进行比较，发现改进后的Duffing系统能够识别出传统方程不能识别的微弱周期信号。通过比较反映出改进Duffing方程对较大固有频率的信号具有更好的识别能力。

2 滚动轴承故障分析

为了验证改进Duffing系统在现场也能够得到应用，本文采用美国凯斯西大学电气工程与计算机科学系轴承实验数据[10]进行实验。测试轴承为6502-2 RS SKF深沟球轴承，分析轴承外圈在转速为1750 r/m in时的故障。外圈故障为人为用电火花加工一个0.007''的微小圆坑故障。其滚动体直径8 mm，节圆直径40 mm，滚动体数9，接触角0°。数据的采样频率为12 000 Hz，采样点N=5 050，发动机转速n=1 750 r/m in。计算所得轴承各部件故障频率如表1所示。

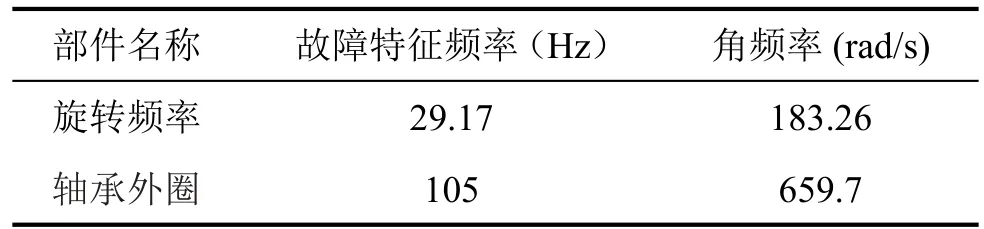
表1 轴承各位置故障频率

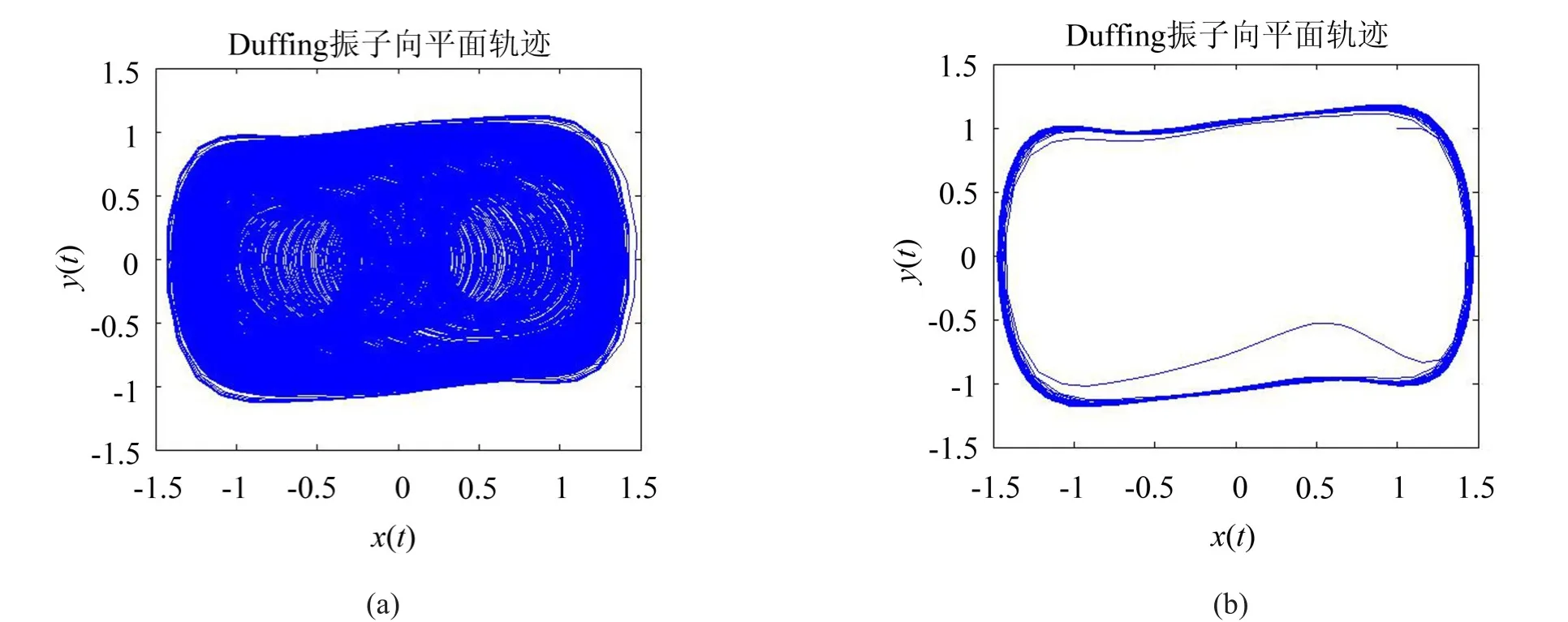
图3 ω=15时改进系统相轨迹图

由于刚开始采集的信号中噪声信号太多，若直接利用Duffing方程进行分析，则大大增加了计算量，为了减少计算时间，在进行混沌分析之前先对采集到的信号进行小波包变换。其处理方案如图4所示。

根据表1可知轴承外圈的故障频率主要在100～140 Hz之间，因此在小波分解时我们可以将其它频段的波过滤掉。现采用Daubechies小波对故障原始数据进行6层分解[10]，由于采样频率为12 000 Hz，故通过小波分解后留下94 Hz～187 Hz频率的数据带入Duffing振子方程进行混沌分析。小波分解前后数据时域波形图如图5所示。

图4 信号处理方案

分别利用wolf方法对传统Duffing振子和改进Duffing振子进行最大Lyapunov指数计算，得到两方程的临界阈值：fr传统=0.731 4，fr改进=0.717 286。根据轴承的参数，传统Duffing方程和改进Duffing方程分别为式（4）、（5）。

将小波降噪后的数据分别利用传统Duffing方程和改进Duffing方程进行进一步的分析，得到的相轨迹图如图6、图7所示。图6是利用传统Duffing方程进行分析得到的相轨迹，图7是利用改进Duffing方程进行分析得到的相轨迹，两图中(a)表示系统未加待测信号时Duffing振子相轨迹，(b)表示系统加入待测信号后Duffing振子相轨迹。通过比较发现，改进Duffing方程在加入待测信号后由临界状态进入到大尺度周期状态，而传统Duffing方程在加入待测信号后仍然处于混沌状态。

图5 轴承小波降噪前后时域波形图

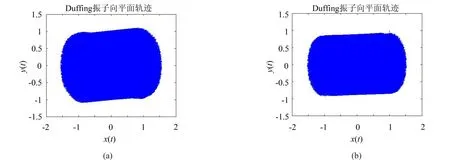
图6 传统Duffing振子检测轴承故障相轨迹图

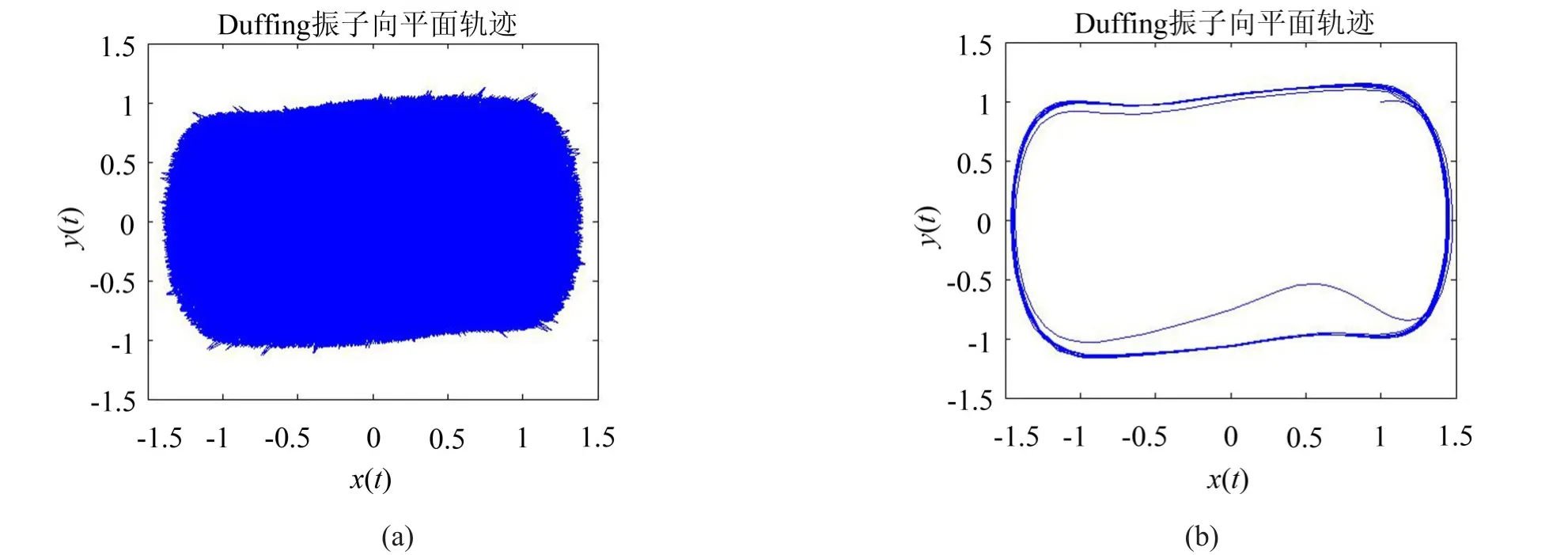
图7 改进Duffing振子检测轴承故障相轨迹图

通过比较发现，改进Duffing方程在加入待测信号后由临界状态进入到大尺度周期状态，而传统Duffing方程在加入待测信号后仍然处于混沌状态。上述实验验证了本文改进的Duffing振子方程可应用于滚动轴承故障诊断。

3 结语

通过对传统Duffing方程和改进Duffing方程进行仿真实验对比，并利用两种方法对轴承外圈故障信号进行检测。结果表明改进Duffing方程能够很好的反映轴承外圈确实存在故障状态，而传统Duffing方程无法将轴承故障显现出来。从而验证了改进Duffing系统对于轴承故障微弱信号检测的有效性。该方法具有简单、直观、便于实现的特点，在轴承故障诊断方面具有很好的应用前景。

[1]苏新伟.基于小波理论的滚动轴承振动信号的分析研究[D].哈尔滨：哈尔滨工程大学，2011年.

[2]郭玉秀，倪晓红，王玉田.基于混沌弱信号检测的轧机故障诊断研究[J].工程设计学报，2011，18(3)：218-221.

[3]张勇，纪国章.基于混沌振子和小波理论的轴承故障诊断方法[J].轴承，2010，(5)：53-55.

[4]李久彤，姜万录，王益群.齿轮早期故障的间歇混沌诊断方法[J].燕山大学学报，1999，23（3）：219-222.

[5]朱夜明，乔宗敏.一道数学建模问题的Matlab求解方法[J].安庆师范学院学报，2006，12（1）：42-45.

[6]Hafstein S.F.A constructive converse Lyapunov theorems on asymptotic stability for nonlinear autonomous ordinary differential equations[J].Dynam ical Systems,Sep.,2005, Vol.20（No.3）:281-299.

[7]孙克辉，谈国强，等.Lyapunov指数计算算法的设计与实现[J].计算机工程与应用，2004，（35）：12-14.

[8]李香莲.机械振动微弱慢频变信号的混沌振子检测[J].中国机械工程，2006，17(1)：12-16.

[9]王丽霞.混沌弱信号检测技术[D].哈尔滨：哈尔滨工程大学，2011.

[10]Case western reserve university bearing data center website[OL].http://www.eecs.case.edu/laboratory/ bearing,2013-02-19.

Detection of Weak Fault Signals of Bearings Based on the Improved Duffing Theory

REN Xue-ping,LIU Tong-tong

(Mechanical Engineering School,Inner Mongolia University of Science and Technology, Baotou 014010,Neimenggu China)

The shortcom ing of the fundamental theory of traditional Duffing oscillator chaotic system for weak signal detection is analyzed,and a new method for the detection based on improved Duffing oscillator is proposed.This method can break through the limitation of natural frequency in the traditional method.It can detect the weak signal with large natural frequencies.In this paper,the fault signal of the outer ring of a bearing is analyzed using the traditional and the current improved method respectively.The results show that the improved method can find the weak fault signal better than the other one.The results from simulation signal analysis and bearing fault diagnosis experiments are in good agreement, which shows that the method proposed in this paper is effective.

vibration and wave;chaos theory;Duffing oscillator;improved algorithm;signal detection;bearing fault

TB52

A

10.3969/j.issn.1006-1335.2014.01.039

1006-1355(2014)01-0173-05

2013-03-19

内蒙古自治区自然科学基金项目（基金编号：2012MS0717）

任学平(1963-)，男，河北省阳原人，博士，主要从事机械工程测试与故障诊断研究。

刘桐桐(1988-)，男，济南人，在读研究生，主要从事机械故障诊断与混沌理论研究。

E-mail:liuxiaohang1314277@126.com