傅里叶逆变换模拟路面对车辆平顺性的影响

岳杰，张进秋，宋征，彭志召，贾进峰

（装甲兵工程学院，北京100072）

傅里叶逆变换模拟路面对车辆平顺性的影响

岳杰，张进秋，宋征，彭志召，贾进峰

（装甲兵工程学院，北京100072）

利用Matlab仿真生成各种等级随机路面激励对二自由度履带车辆模型所产生的振动响应，并进行平顺性影响的分析。其间，设计了基于离散傅里叶逆变换生成路面不平度的方法，并对仿真生成的B级和D级路面与标准功率谱进行了对比验证。构建了二自由度车辆模型，利用Simulink软件建立了系统仿真模型，在不同车速、不同路面等级输入下对履带车辆平顺性影响进行了分析。结果表明，路面变差和提高车速都将降低车辆的行驶平顺性。

振动与波；履带车辆；离散傅里叶逆变换；平顺性；振动响应；路面不平度

履带式装甲车辆悬挂系统的弹性特性和阻尼特性都具有很强的非线性，在分析这类车辆的路面行驶时的非线性随机振动时，需要在时域里进行研究[1]。且履带式装甲车辆行驶路面非常复杂，其路面不平度是车辆振动的主要激励源，而这种振动达到一定程度时，不仅会使乘员感觉不舒适或疲劳，而且还会造成车载装备的损坏。因此，研究输入不同路面的随机激励对车辆行驶平顺性的影响显得尤为重要。

本文采用离散傅里叶逆变换方法生成随机路面不平度，并构建了车体振动分析模型，利用悬挂系统参数求出了传递函数，再把随机路面不平度作为输入激励对振动响应进行分析，从而可以评价不同路面和车速下对平顺性的影响。

1 路面不平度数学描述

路面不平度具有随机、零均值、平稳和各态历经的特性，可以用平稳随机过程理论来分析描述[2,3]。在实际工程中，路面不平度可由路面不平度系数拟合的功率谱密度来评价[4]，并可利用统计参数所描述的路面功率谱进行道路模拟、车辆平顺性和悬挂特性的研究。路面不平度的统计特性一般采用位移功率谱密度来描述，其公式为[1]

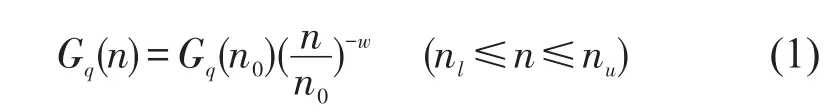
式中n为空间频率，表示每米长度中包含n个波长，单位：m-1；n0为参考空间频率，单位：0.1 m-1；Gq(n0)为参考空间频率n0下的路面谱，称为路面不平度系数，该值取决于车辆行驶的路面等级，单位为m2/ m-1；w为频率指数，它决定路面谱的频率结构，通常取2；nu，nl分别表示路面谱的上下限空间频率。

上下限空间频率的选取要保证车辆以常用速度行驶时由路面不平度激起的振动频率范围，包含车辆系统振动时的主要固有频率。车辆受到的激振频率为：f=n·v。f为输入的时间频率；v为车辆行驶速度。如果车辆振动的主要固有频率范围为(fl，fu)，行驶速度范围为(vl，vu)，便可得出路面不平度功率谱密度的上下限空间频率nu和nl，分别为fu/vl，fl/vu。

2 逆变换生成路面不平度

频域信号通过傅里叶逆变换就可得到时域信号，傅里叶逆变换法的基本思路是由己知路面功率谱求得与其对应的一系列离散傅里叶变换的模值，然后用正态分布的随机序列经傅里叶变换后得到的相位谱作为相角输入，构造出频域信号，再对其进行傅里叶逆变换就得到路面不平度随机序列[5,6]。对获得的随机序列反求功率谱密度能够与理论值相符合，保证了该变换方法模拟路面不平度的精度。路面样本实际采样信号是离散的并且采样信号的样本长度是有限的，对路面样本进行离散傅里叶变换，其表达式为

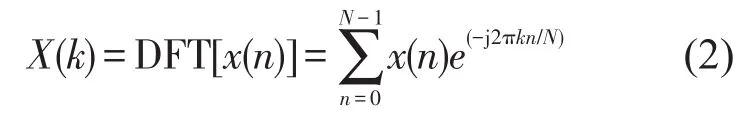
式中X(k)为采样序列x(n)的离散傅里叶变换，k=0,1,2,...N-1，n=0,1,2,...N-1。其中N为数据点采样长度，采样间隔为Δl，采样周期T（即总采样距离L）T=L=N·Δl，最小频率间隔为Δn=1/T，某空间频率nk对应的谱线序号为k，nk=k/NΔl；由于实际工程信号采用单边功率谱，且路面不平度随机信号属于能量有限信号，因而X(nk)=ΔlX(k)。根据Parseval定理，采用Cooley-Turkey法[7,8]计算的路面不平度的位移自功率谱密度Gq(nk)为

根据(2)(3)式得

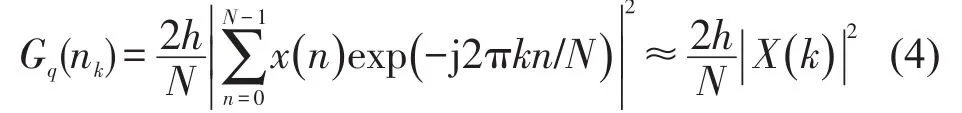
该式即为实测路面不平度数据的功率谱密度的计算式。根据上式可以得到离散傅里叶变换模值为

而与时域序列x(n)对应的X(k)是复数，若相角为φk，φk可以在[] 0,2π内随机选取。则有

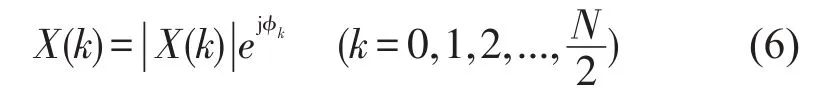
由(5)(6)式可知,对具有N个数据的离散时域序列x(n)（n=0,1,2,...,N-1），其离散傅里叶逆变换有N个数据,但在计算其功率谱密度时只需其前(N+1)/2个数据。现在利用(5)(6)式可得到其离散傅里叶变换的前(N+1)/2个数据,所以若要通过逆变换得出离散时域序列x(n)，就必须根据其特性补齐后部分数据。

对由(6)式得到的N/2+1个离散傅里叶变换值X(k)(k=0,1,2,...,N/2)基于共轭关系进行补齐，可以得到X(k)(k=0,1,2,...,N-1)。最后对X(k)进行离散傅里叶逆变换得到路面不平度随机序列：

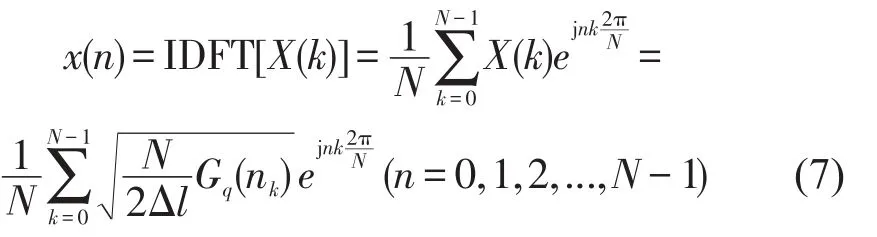
3 模拟路面生成

3.1 有效空间频带

履带车辆质心垂直振动的固有频率约1.5 Hz，负重轮的垂直振动固有频率约为30 Hz，而由履带板连接处不平所引起的激励频率在高速时由于远离负重轮固有频率而忽略不计[1]。选取时间频率下限为0.5 Hz，上限频率为30 Hz，便可覆盖其固有频率。履带车辆只在A级或B级路面上行驶时能够达到最高车速约为(70～80)km/h，而车辆平均速度一般约为最高速度的60%～70%（约为42 km/h～56 km/h），相当于车辆在C级至D级路面行驶时速度达到50 km/h。考虑行驶等级路面情况，车速u=(21.6～72)km/h即（6～20 m/s）。因此，模拟路面不平度的上限频率nu为5 m-1,下限频率nl为0.025 m-1。

依据采样定理，空间采样频率应大于模拟路面的截止频率的2倍，则有(1/Δl)≥2 nu，可得Δl≤0.1 m。为保证在计算离散的功率谱密度时其下限频率准确，则有nl≥Δn，即总采样距离L≥1/nl，可得L≥40 m。因此，采样间隔Δl取0.05，总采样距离L取500 m，可以满足以上要求。因此有采样点数N=L/Δl=10 000，空间最小频率间隔Δn=1/L=0.002。仿真参数如表1所示。

3.2 数值仿真与分析

利用Matlab仿真工具，按照傅里叶逆变换方法生成路面不平度，其相位角由randn函数产生。按功率谱密度公路路面分为A～H共8个等级，根据统计我国高等级公路基本属于A、B、C3个等级[9]。本文针对履带车辆行驶路面情况，对B级和D级路面的不平度进行研究，仿真生成B级和D级路面不平度，如图1、图2所示。图上的横坐标是沿着道路行驶方向的路面长度，纵坐标是路面相对于基准平面的路面不平度。

图1 B级路面的不平度曲线

图2 D级路面的不平度曲线

通过对500 m路面的仿真结果可以得出，傅里叶逆变换法生成的B级路面不平度峰值范围约为8～15 mm，而数据相对均值的散布程度方差为5 mm；生成的D级路面不平度峰值范围为40～60 mm，方差为20.2 mm。

3.3 功率谱对比验证

为验证基于傅里叶逆变换方法的正确性，根据仿真结果，分别把模拟的路面不平度功率谱密度曲线与标准谱进行对比，如图3、4所示。图中坐标系采用双对数坐标，横坐标是空间频率，纵坐标是功率谱密度。采用该方法生成的路面不平度功率谱密度曲线与标准谱直线都能较好的重叠，证明所采用方法的正确性。其模拟路面不平度数据是由给定功率谱密度经过严密的推导计算和仿真得出的，所用理论分析与计算保证了路面不平度的功率与给定功率谱密度完全一致。因此，本文采用傅里叶逆变换方法生成模拟路面并作为输入激励应用到履带车辆平顺性仿真分析中。

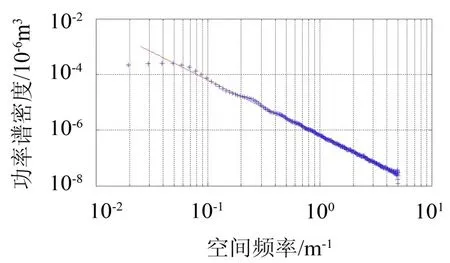
图3 B级路面功率谱密度比较图

图4 D级路面功率谱密度比较图

4 振动响应分析

4.1 基本假设

履带车辆行驶路面比较复杂，要承受复杂的路面激励，其振动响应为随机振动。进行悬挂系统建模时可假设：车辆在规定的匀速条件下行驶，路面的不平度是各态历经随机过程，行驶过程中路面是刚体，不平度不产生变化；车上各轮子悬挂的减振器阻尼和弹性特性相同，悬挂刚度和阻尼系数相同；扭力轴刚度和减振器阻尼系数可等效换算到垂直方向；车体与负重轮均为刚体，且仅考虑垂直方向运动；不计履带影响，前后轮各自独立，相互不产生耦合作用；负重轮胶圈有相同的线性弹性特性，忽略阻尼。

表1 路面激励仿真参数表

4.2 车辆模型建立

为研究车辆行驶的平顺性，在考虑负重轮胶圈刚度的情况下，可建立双质量二自由度车辆振动系统简化模型[10]，如图5所示。

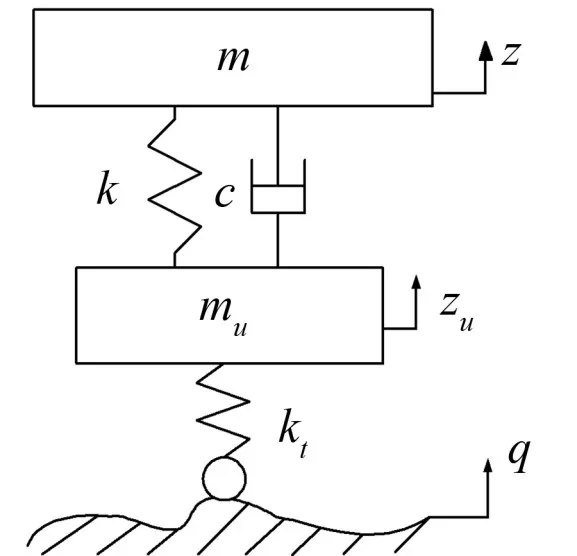
图5 车辆二自由度模型

图5中，m为悬挂质量（车体）；mu为非悬挂质量（负重轮）；k和kt分别为悬挂和负重轮胶圈刚度；c为减振器阻尼系数；q为路面不平度激励；z和zu分别为车轮和车体垂直位移。其动力学方程为

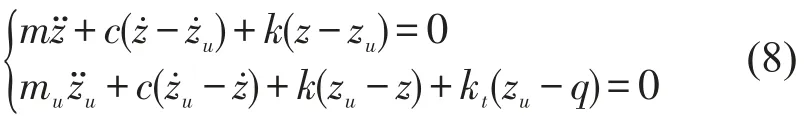
对式（8）两个方程分别进行Laplace变换，并整理得车体位移与路面不平度的传递函数

4.3 系统建模

为得到车体在随机激励下的振动响应，首先把模拟的空间频率路面不平度q(x)转换为不同车速下的时间频率路面不平度q(t)，将表2所列某型履带车辆悬挂参数代入式(9)，通过Simulink仿真软件建立系统模型，如图6所示。

输入路面随机激励q(t)后，再经过线性传递函数模型模块及2个微分模块后，可输出车体垂直振动加速度响应，对其输出信号进行均方根计算后，即可进行行驶平顺性分析。

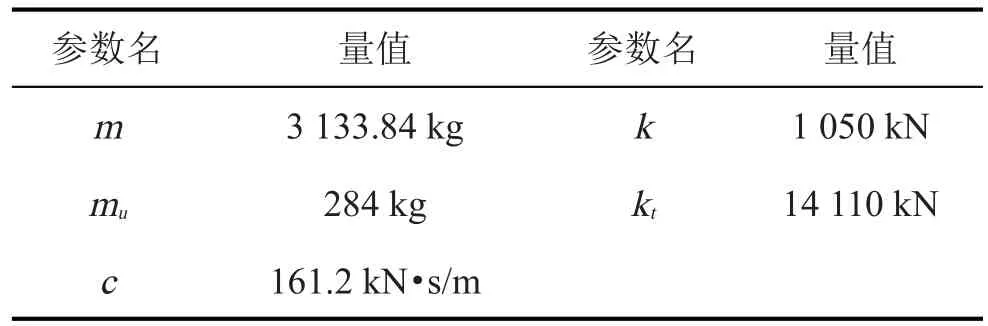
表2 车辆悬挂系统具体参数

5 平顺性评价

5.1 评价指标

采用随机激励输入来评价平顺性时，根据ISO 2631规定，可以考虑对座椅支承面上X、Y、Z轴三个方向平移振动时加权加速度均方根值来评价，而对健康的影响评估应沿各个坐标轴方向独立进行[11,12]。当振动波形峰值系数小于9时，用加权加速度均方根值的基本评价方法来评价振动对人体舒适和健康的影响。所以，实际测试中振动评价应有加速度的测量，对垂直振动，加权加速度均方根值应按下式计算

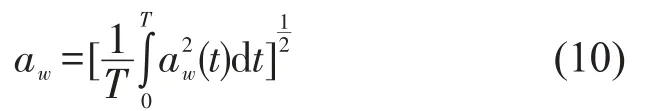
上式中aw(t)为加权加速度时间历程。考虑到影响平顺性的主要因素是车身的垂直振动，其值越小，乘员感觉越舒适，平顺性越好。因此，本文用车体垂直加速度均方根值来代替座椅支承面加速度来评估随机路面对平顺性的影响。

5.2 仿真分析

根据建立的车辆系统模型，对平顺性评价仿真研究采用方法为：基于不同速度和路面不平度生成时域的模拟路面，通过仿真得出车辆驾驶员位置底甲板处车体的垂直加速度，如图7、图8所示，从而分析出各种等级随机路面激励对平顺性的影响程度。

图6 车辆悬挂系统结构图模型

图7 B级路面下不同车速加速度曲线对比图

图8 D级路面下不同车速加速度曲线对比图

选取B、D级两种路面下各种速度对应的加速度均方根值进行仿真对比，从图7、图8可以得出，路面等级确定时，随着车速的增加，车体的加速度均方根值呈逐渐增加趋势，而路面等级越差增加越明显；当车速不变时，随着路面等级的增加，车体的加速度均方根值呈逐渐增加趋势。当履带车辆分别以三档21.6 km/h、五档36 km/h车速下行驶时，分别对8级路面高程变化下的加速度均方根值进行仿真对比发现，随着路面等级的增加，路面不平度峰峰值逐渐增大，加速度均方根值呈线性关系；当车速变化增加时，同一路面下加速度均方根值也是逐渐增加的。

6 结语

采用离散傅里叶逆变换原理，生成各级模拟路面，通过构建两自由度履带车辆力学模型，利用仿真输出加速度信号进行平顺性评价。具体研究包括：

（1）利用傅里叶逆变换方法进行路面不平度的模拟。功率谱对比表明，模拟较为准确；

（2）基于双质量车辆模型构建了系统仿真结构图，可以进行振动响应分析；

（3）仿真结果表明，平顺性不仅与路面不平度有关，还与车速有很大关系。当路面变差与车速提高时，车体加速度均方根值均呈现增长的趋势，且路面等级的变化是引起乘坐舒适性下降的主要因素。

[1]丁法乾.履带式装甲车辆悬挂系统动力学[M].北京：国防工业出版社，2004：13-81.

[2]金睿臣，宋健.路面不平度的模拟与汽车非线性随机振动的研究[J].清华大学学报(自然科学版)，1999，39 (8)：76-79.

[3]Schiehlen W,HU B.Spectral simulation and shock absorber identification[J].International Journal of Non-linear Mechanics,2003,38:161-171.

[4]GB/T7031-2005.机械振动:道路路面谱测量数据报告[S].北京：中国标准出版社，2005.

[5]刘献栋，邓志党，高峰.基于逆变换的路面不平度仿真研究[J].中国公路学报，2005，18(1)：122-126.

[6]刘献栋，邓志党，高峰.公路路面不平度的数值模拟方法研究[J].北京航空航天大学学报，2003，29(9)：843-846.

[7]王新明，王秉纲.高速公路路面功率谱[J].交通运输工程学报，2003，2(3)：53-56.

[8]邬惠乐，邱毓强.汽车拖拉机试验学[M].北京：北京机械工业出版社，1981：299-379.

[9]赵济海，王哲人.路面不平度的测量分析与应用[M].北京：北京理工大学出版社，2000：1-16.

[10]余志生.汽车理论[M].北京：机械工业出版社，2000：203-251.

[11]GB/T 13441.1-2007.机械振动与冲击：人体暴露于全身振动的评价[S].北京：中国标准出版社，2007.

[12]GB/T4970-1996.汽车平顺性随机输入行驶试验方法[S].北京：中国标准出版社，1996.

Simulation of Influence of Road Roughness on Vehicle’s Ride Com fort Based on Inverse Discrete Fourier Transform

YUE Jie,ZHANG Jin-qiu,SONG Zheng,PENG Zhi-zhao,JIA Jin-feng

（Academy ofArmored Forces Engineering,Beijing 100072,China)

Various levels of random road excitation are simulated by means of MATLAB.And the vibration response of a 2-DOF vehicle model under this excitation is obtained and analyzed.The chassis vibration response is used to evaluate the ride com fort of tracked vehicles.The method for generating different road roughness is studied and designed based on the inverse discrete Fourier transform(IDFT)method.The grade B and grade D road spectra are compared with typical power spectra to verify the feasibility of this method.The 2-DOF tracked vehicle’s suspension model is constructed and the system simulation model is built by Simulink software.Inputting different kinds of vehicle velocity and road roughness into the model,the vehicle’s ride com fort is computed and analyzed.It is found that the road stochastic excitation will have large influence on ride com fort of the tracked vehicle.Increasing of the road roughness level and the vehicle’s speed will greatly reduce the vehicle ride com fort.

vibration and wave;tracked vehicle;IDFT;ride com fort;vibration response;road roughness

TB52；TP391.9；TJ811

A

10.3969/j.issn.1006-1335.2014.01.030

1006-1355(2014)01-0132-05

2013-03-25

军队科研计划项目

岳杰（1985-），男，四川眉山人，博士研究生，目前从事车辆工程、车辆振动控制研究。

E-mail:yuetank@163.com