结构参数对轴承振动噪声的影响

殷玉枫，张建水

（太原科技大学机械工程学院，太原030024）

结构参数对轴承振动噪声的影响

殷玉枫，张建水

（太原科技大学机械工程学院，太原030024）

根据非线性力学和声学理论，建立轴承结构本身产生振动噪声的数学模型，分析轴承结构参数（径向游隙、沟道曲率半径、钢球个数）对轴承振动噪声的影响。研究表明：径向游隙对轴承振动噪声的影响最为显著，并呈现很好的线性关系。沟道曲率半径对振动噪声的影响复杂，它对轴承振动位移和速度最大幅值的影响各不相同，随着沟道曲率半径的增加，最大声压、最大声压级逐渐减小；从整体出发，在符合设计条件的前提下，减小钢球个数可以减小轴承的振动噪声。x方向的振动噪声远大于y方向，由此，结构参数对x方向的振动噪声的影响更为显著。通过改变结构参数来减振降噪，比起传统方法简单、可行、有效，减少制造成本，为以后轴承减振降噪提供一种新的方向和一定的参考依据。

振动与波；滚动轴承；结构参数；振动；噪声

滚动轴承振动与噪声自1950年起就开始成为人们关注的问题，迄今已取得众多的研究成果。解决该问题的基本方向是改善轴承制造工艺，即提高滚动体及套圈的几何精度[1―3]，降低工作表面的粗糙度[4―6]，采用各向同性的钢材[7―9]，使用洁净度高的润滑材料[10,11]，洁净的装配条件，恰当的安装和使用条件。随着高精度、低噪声轴承的发展，轴承精度超过某一界限时，轴承的振动水平不是由轴承自身的误差来决定，即使轴承不存在几何误差，其他条件都在理想状况下，轴承仍产生着由其结构特点所决定的振动与噪声[12]。

对于轴承结构引起的振动及噪声，参考文献[12]阐述了轴承结构振动产生的原因，同时介绍了理论计算方法及其模拟实验；参考文献[13]利用声学理论建立噪声数学模型。多数研究的目的只在于振动与噪声，并未去探究结构参数对轴承振动噪声的影响。本文根据非线性力学和声学理论，建立振动噪声数学模型，分析结构参数（径向游隙、沟道曲率半径、钢球个数）对轴承振动噪声的影响。

1 轴承结构的非线性振动

1.1 轴承非线性接触力

径向游隙为零的情况下，轴承受径向负荷Fr作用时，轴承中受载最大的滚动体负荷为

式中Z——钢球个数。

有径向游隙时，受负荷区域将减小，滚动体的接触负荷增加，此时可以近似计算轴承中受载最大的滚动体负荷

不考虑套圈的弯曲变形，由角度ψ处的变形协调条件

式中ψ——滚动体中心线与径向载荷作用线的夹角；δψ——与径向负荷作用线夹角为ψ处的总弹性变形量；δmax——滚动体最大弹性变形量。

接触负荷和变形量的关系为：

式中Kn——接触刚度；Qψ——与负荷作用线夹角为ψ位置的滚动体承受的接触负荷。

由式（3）、（4）可以得到

即

1.2 轴承振动模型

如图1，假设轴承系统内圈转动，外圈不动。滚动轴承振动的基本形式是钢球滚动引起的弹性接触振动，它是结构决定的轴承的固有特性[14]。因此，轴承的振动方程建立在滚动体的基础上。

图1 轴承振动模型示意图

式中wc——滚动体的公转角速度。

第j个滚动体接触点的角位移为：

当第j个滚动体位于角ψj时，其弹性接触变形量

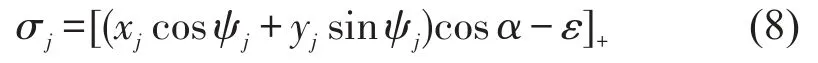
式中x——滚动体中心在垂直方向的位移；

y——滚动体中心在水平方向的位移；

ε——径向游隙；a—接触角。

下标“+”表示：当δj≤0时，第j个滚动体没有产生接触变形；当δj≥0时，接触弹性变形为δj。

将（8）代入（4），得到第j个滚动体的非线性接触力

将其分解到水平方向和垂直方向有

拉格朗日方程是建立系统振动微分方程的普遍方法。利用拉格朗日方程可以比较简单的方式推导得到用广义坐标表示的振动系统的运动微分方程。对一个n自由度系统，拉格朗日方程可以表示为

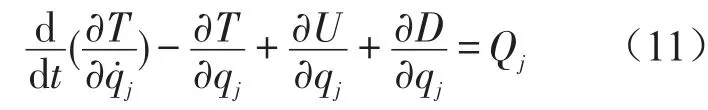
式中T——系统动能；U——系统势能；

D——系统能量耗散函数，对粘性阻尼，瑞利耗散函数与速度平方成正比；

Qj——相对于广义坐标qj的非保守广义力。

根据拉格朗日方程建立第j个滚动体的振动方程为

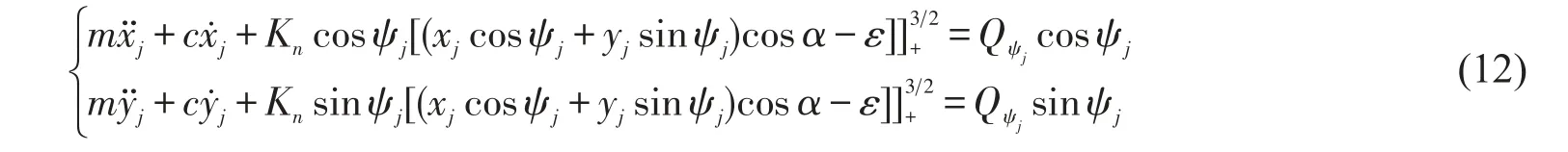
式中：m——滚动体的质量；

c——由于油膜和摩擦造成的粘滞阻尼。

2 轴承非线性接触的噪声模型

2.1 声学理论

设有一半径为r0的球体，其表面在作均匀的微小胀缩振动，即表面在半径r0附近以微量位移作简谐振动，带动毗邻的介质质点随之振动，从而在其周围辐射声波，见图2。因为由它辐射的声波波阵面是其声压通解为均匀球面的，辐射的是均匀球面声波。

声波方程为

图2 球振图

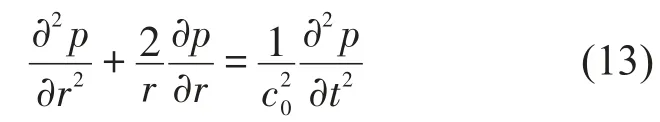
其声压通解为

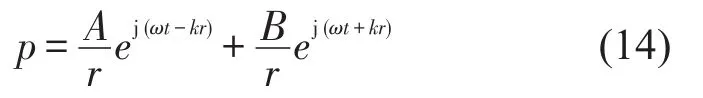
式中A、B——待定常数；w——声波角频率；

式（14）第一项代表从球源向外辐射（发散）的球面波，第二项代表从远处向球源反射（会聚）回来的球面波。现在讨论向无界空间辐射的自由行波情形，假定空间不存在反射面，因而没有反射波，这时常数B可以确定为B=0，式（14）可简化表示成

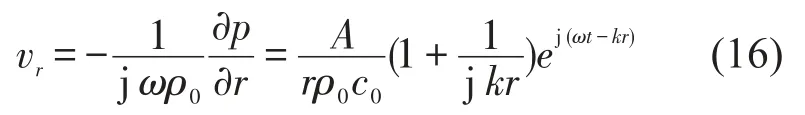
式中：ρ0——介质密度；c0——声速；r——振源到测点的距离。

在脉动球源辐射声场的公式中有一待定常数A，它可由球声源表面的振动情况，即球源的边界条件来确定。因为声场是由球源产生的，所以其辐射声场的特性自然也应于球源的振动有关。径向坐标r的质点速度

2.2 轴承噪声模型

将滚动体的振动表面看作是脉动球源。脉动球源是表面作均匀胀缩振动的一种球面声源，也就是在球源表面上各点沿着径向作同振幅、同相位的振动。

设在球源表面的振动速度为

式中ua——速度的幅值；k r0——初相位。

在球源表面处介质质点速度应等于球源表面的振速：

由式（15）、（16）、（17）、（18）可得到脉动球源所辐射的声压为

如图3，设测点位于三维坐标系中某一位置(x0, y0，z0)，如图3所示，第j个滚动体到测点的距离为

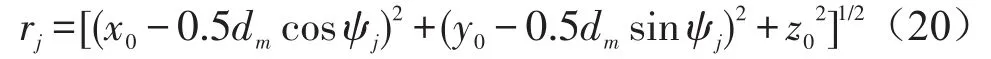
式中dm—钢球的节圆直径。

图3 轴承噪声模型

测点得到的滚动体振动产生的合成有效声压平方为

第j个滚动体的声压级为

式中：p0—基准声压。

总声压级：

3 结构参数对轴承振动噪声的影响

根据建立的数学模型，以6206轴承为例进行分析，轴承的结构参数见表1。单个滚动体质量m= 3.5 g，润滑阻尼c=30 Ns/mm，径向力Fr=5 000 N，滚动体的公转角速度w=100 rad/s，接触角a=0，测点位于点（0.5 m，0.5 m，0.5 m）处，介质密度ρ0=1.21 kg/m3，声速c0=343 m/s，基准声压P0=2×10-5Pa。下面基于单一变量法分别来研究结构参数对轴承振动噪声的影响。

3.1 径向游隙的影响

游隙是滚动轴承的主要结构参数之一，它对轴承振动噪声将产生重要的影响。轴承制造厂生产出的轴承原始游隙应符合标准规定。标准规定了各类轴承的游隙组别和各组的游隙值。深沟球轴承的径向游隙，标准规定有2组、0组（基本组）、3组、4组、5组，共5个组别。0组适用于一般工作条件，要优先选用。通过查表，6206轴承的0组游隙值为6 um～20 um[16]。

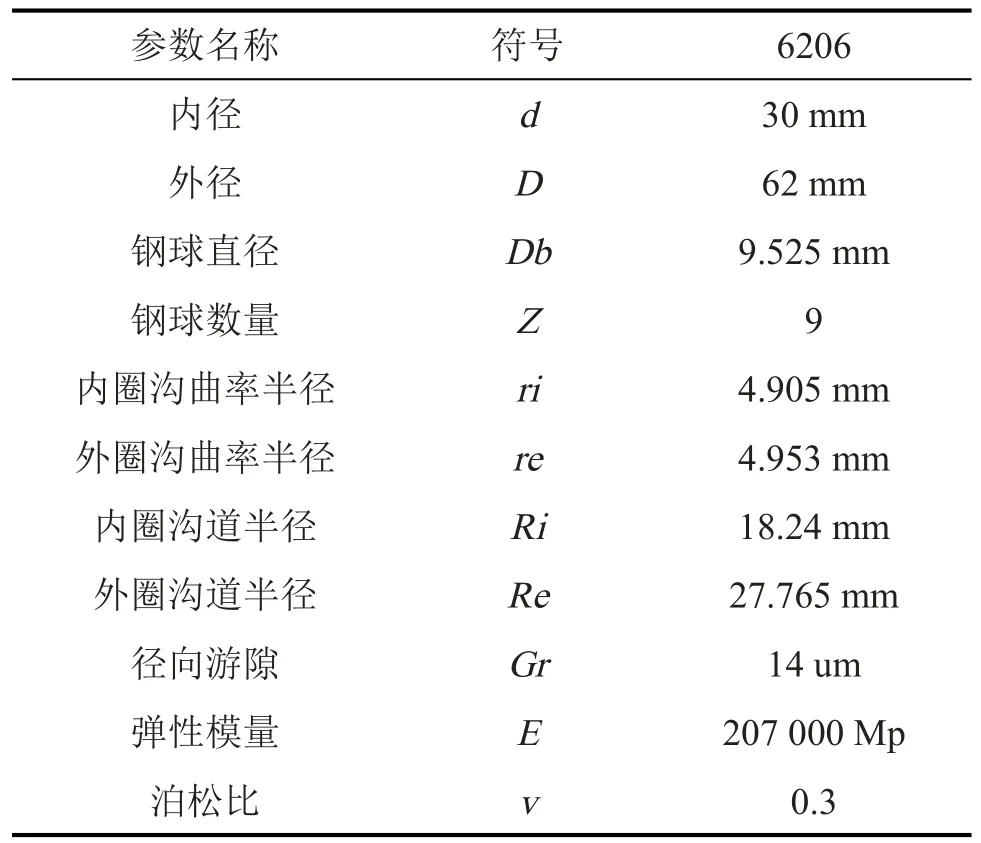
表1 6206轴承的结构参数[15]

下面径向游隙分别取为8 um、14 um、20 um来分析径向游隙对轴承振动噪声的影响。对应的具体数据见表2、图4。

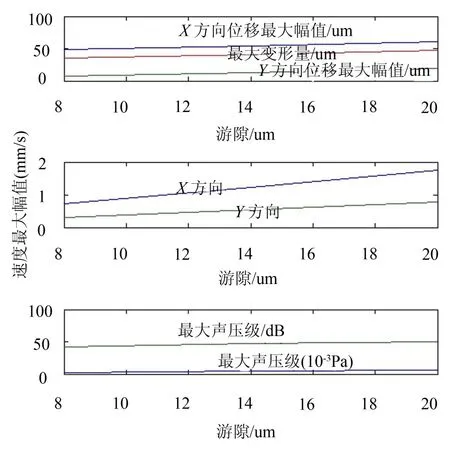
图4 游隙对单个滚动体振动噪声的影响

从分析数据可以看出，随着径向游隙的加大，振动噪声随之增强，并且径向游隙与振动噪声的位移最大幅值、速度最大幅值、最大声压、最大声压级及最大变形量的关系呈现很好的线性关系。

3.2 沟道曲率半径的影响

在建立的理论模型中，沟道曲率半径与接触刚度相关，进而影响轴承的振动噪声。沟道曲率半径的取值不固定，一般取为球径的51%～53%。下面对沟道曲率半径对轴承振动噪声的影响进行分析，详细数据见表3。

根据分析结果显示：随着沟道曲率半径的增加，接触刚度逐渐减小，从而最大变形量逐渐增大；随着沟道曲率半径的增加，x方向位移最大幅值逐渐增加，但速度最大幅值逐渐减小；随着沟道曲率半径的增加，y方向位移最大幅值逐渐减小，但速度最大幅值逐渐增加；随着沟道曲率半径的增加，最大声压、最大声压级逐渐减小。

3.3 钢球个数的影响

钢球个数变化直接影响轴承所受的负荷，进而影响轴承的振动噪声。下面对钢球个数对轴承振动噪声的影响进行分析，详细数据见表4。

从计算结果可以看出：增加钢球个数，使钢球承受的径向载荷减小，从而减小单个钢球的振动噪声。但从整个轴承来看，增加钢球个数就会增加振动噪声源的数量，将会增加轴承的振动噪声。以上数据可以显示，增加钢球个数，确实可以减小单个滚动体的振动噪声，但减小幅度比较小，在加上增加钢球个数就会增加振动噪声源的数量，将会增加轴承的振动噪声。因此，从整体出发，在符合设计条件的前提下，减小钢球个数可以减小轴承的振动噪声。

3.4 降噪效果

通过以上研究结果，下面仍以6206轴承为例进行分析，通过计算数据来显示降噪的效果。根据3.1部分的论述，径向游隙取6 um；根据3.2部分的论述，内、外沟道曲率半径取5.048 25；研究单个滚动体降噪的效果，滚动体个数和表1取值相同。与表1中的轴承相比，具体数据见表5。

表2 游隙对单个滚动体振动噪声的影响

通过计算结果可以看出：常用结构参数的轴承最大声压为4.644×10-3Pa，最大声压级为47.319 dB；优化后结构参数的轴承最大声压为1.957×10-3Pa，最大声压级为39.814 dB。最大声压减小量为2.687× 10-3Pa，降低57.85%；最大声压级减小量为7.505 dB，降低15.86%。通过以上数据充分显示：通过改变结构参数来减振降噪，是一种简单、可行、有效的方法。

4 结语

本文结合非线性振动理论和声学理论，建立振动噪声数学模型，分析由轴承结构引起的振动与噪声。从具体的结构参数（径向游隙、沟道曲率半径、钢球个数）入手，分析对轴承振动噪声的影响。研究表明：

（1）径向游隙对轴承振动噪声的影响最为显著。随着径向游隙的加大，振动噪声随之增强，并呈现很好的线性关系；

（2）沟道曲率半径对轴承的振动位移最大幅值、速度最大幅值的影响作用不同，随着沟道曲率半径的增加，最大声压、最大声压级逐渐减小；

表3 沟道曲率半径对单个滚动体振动噪声的影响

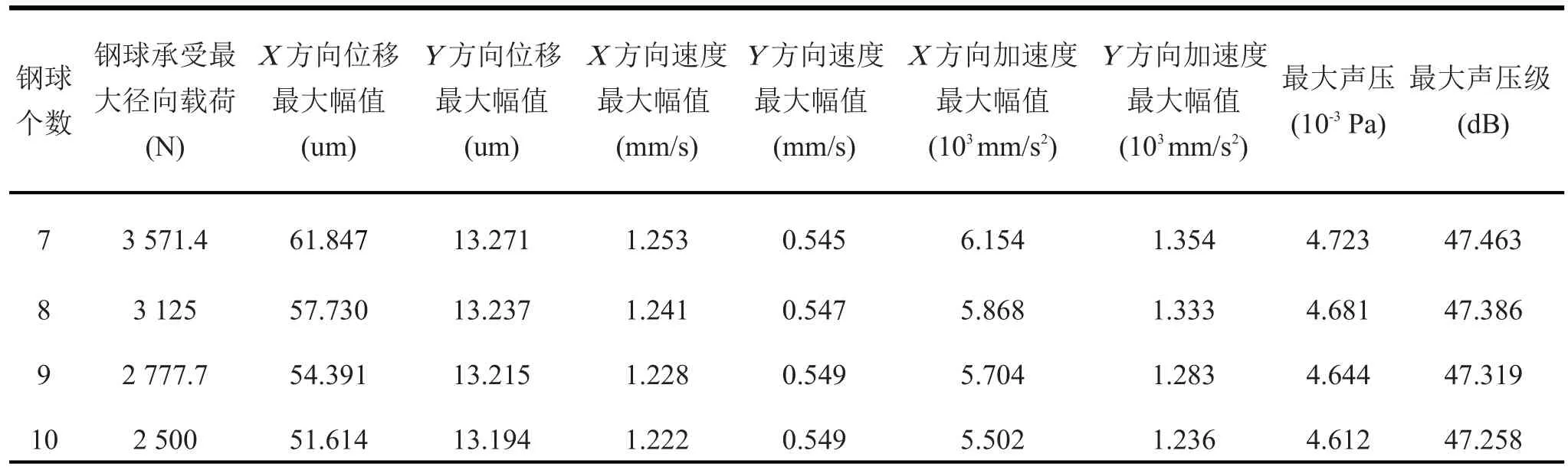
表4 钢球个数对单个滚动体振动噪声的影响

表5 单个滚动体降噪效果

（3）增加钢球个数可以减小单个钢球的振动噪声，但从整个轴承来看，增加钢球个数就会增加振动噪声源的数量。因此，从整体出发，在符合设计条件的前提下，减小钢球个数可以减小轴承的振动噪声；

（4）从计算结果可以看出，x方向的振动噪声远大于y方向，占主导地位。结构参数对x方向的振动噪声的影响更为显著。

通过改变结构参数来减振降噪，比起传统方法（改善轴承制造工艺）简单、可行，减少制造成本，为以后轴承减振降噪提供一种新的方向和方法。以上研究可以为滚动轴承设计和结构振动噪声机理研究及噪声控制提供一定的参考依据，为进一步探讨滚动轴承振动噪声与各种因素的量化关系奠定基础。

[1]苗晓鹏，夏新涛.滚子轴承减振降噪技术的探讨[J].安阳工学院学报，2005(5)：15-17.

[2]杨进周，孙立明，梁忠.深沟球轴承降噪工艺[J].轴承，2000(3)：14-18.

[3]郭萍，吉洪涛.6205JD2/C303轴承套圈磨超加工工艺[J].轴承，2005(1)：13-14.

[4]殷玉枫,张闯.表面波纹度激励下的滚动轴承非线性接触噪声分析[J].噪声与振动控制，2010(1)：43-47.

[5]M c Fadden P D,Sm ith J D.The vibration produced by multiple point defects in a rolling element bearings[J].Journal of Sound and Vibration,1985,98(2):263-273.

[6]张文平，吴云鹏.基于表面特征的滚动轴承振动模型研究[J].哈尔滨工程大学学报，2007(28)：528-531.

[7]Chakraborty J,Bhattacharjee D,Manna I.Austempering of bearing steel for improved mechanical properties[J].Scripta Materialia ,2008,59:247-250.

[8]Hetzner D W,Geertruyden W V.Crystallography and metallography of carbides in high alloy steels[J].Materials Characterization ,2008,59:825-841.

[9]Zalikanova I P.Use of damping alloys based on iron to reduce noise from impacts[J].Metallurgist,2008,52(3-4): 205-206.

[10]刘庆廉，吴宝杰，李辉峰.润滑脂对轴承噪声影响因素探讨[J].轴承，2001(1)：23-26.

[11]赵联春，马家驹，马纯青.润滑对球轴承振动特性的影响[J].摩擦学学报，2003，23(5)：421-425.

[12]马纯，刘春浩，赵联春.滚动轴承的结构振动[J].哈尔滨轴承，2003，24(2)：17-22.

[13]付刚，夏新涛，孙立明.轴承结构引起的固有振动所产生的噪声数学模型的确定[J].机械，2003，30(1)：10-12.

[14]赵联春，马家驹.球轴承的弹性接触振动[J].机械工程学报，2003,39(5)：60-64.

[15]冈本纯三，黄志强.球轴承的设计计算[M].北京：机械工业出版社，2003.

[16]陈龙，颉潭成，夏新涛.滚动轴承应用技术[M].北京：机械工业出版社，2010.

Effect of Structural Parameters on Vibration Noise of Rolling Bearings

YIN Yu-feng,ZHANG Jian-shui

（School of Mechanical Engineering,Taiyuan University of Science and Technology, Taiyuan 030024,China）

A mathematical model for vibration and noise analysis of rolling bearings is established based on the theory of nonlinear dynam ics and acoustics.The effects of structural parameters on the vibration noise are analyzed.The research results show that radial clearance is the most significant factor which affects the vibration noise.The effects of the channel curvature radius on the amplitudes of vibration displacement and velocity are different.The maximum sound pressure and the maximum sound pressure level decrease gradually with the increasing of the channel curvature radius.The bearing noise can be reduced by reducing the number of the steel balls in the bearing.The noise in the x-direction is much larger than that in the y-direction.Comparing with the traditional method,the method by changing the structural parameters to reduce the noise is simple,feasible,effective and econom ic.This research provides a new approach for noise reduction of bearings and a foundation for further study of the quantitative relationship between the vibration noise and the structural parameters of bearings.

vibration and wave;rolling bearing;structural parameter;vibration;noise

TB52；TH133.3

A

10.3969/j.issn.1006-1335.2014.01.018

1006-1355(2014)01-0076-06

2013-02-27

山西省科技攻关项目资助(基金编号：20100321058-01)

殷玉枫（1963-），男，教授，主要研究方向：振动与噪声控制，非线性动力学，机械设计及理论。

E-mail:yinyufeng_ty@163.com