北斗系统伪距多径特征及对其定位精度影响分析

翟 勇，张 锋，沈 菲

（北京卫星导航中心，北京100094）

1 引言

我国北斗卫星导航系统（BeiDou navigation satellite system，BDS）已经初步建成，目前在轨卫星14颗，其中包括5颗地球静止轨道（geostationary earth orbits，GEO）卫星、5颗倾斜地球同步轨道（inclined geo－synchronous orbits，IGSO）卫星和4颗中圆地球轨道（medium earth orbits，MEO）卫星，基于BDS混合星座导航体制的应用研究引起了国内外众多学者的关注。

在对BDS定位性能分析评估过程中，发现伪距多径是引起定位误差较大的主要因素。BDS伪距多径不仅涉及到卫星星座布局和用户具体使用环境，而且还受到卫星发射信号带宽、接收机预相关带宽和内部资源的约束，在空间上相关性很小，不能通过差分技术进行修正［1］。尽管采取了大量抗多径措施，仍然难以消除多径误差影响。

目前，基于相干超前减滞后延迟锁定环的码跟踪多径误差包络是公认的多径误差评判标准［2-3］，国内外众多文献基于上述标准对全球定位系统（global positioning system，GPS）信号多径特性进行了大量研究，但BDS导航信号的多径误差特性及影响因素尚未深入研究，不同型号北斗民用接收机抗多径性能指标尚未深化论证，实测环境下多径误差对BDS定位性能影响尚未全面分析。

鉴于BDS伪距多径研究需求，本文的工作主要包括：首先，基于BDS民用I支路信号和多径误差包络模型，从理论上研究了BDS不同频点信号多径特性及相关因素；其次，利用BDS模拟信号源和各种型号北斗民用接收机，仿真分析了不同用户机厂家的抗多径效果；最后，通过实测数据分析了BDS伪距多径大小及对定位性能的影响。可为分析BDS多径信号特性和提升接收机抗多径性能提供参考。

2 多径误差包络模型

直视信号和多径信号组成的复合中频信号可以表示为［4］

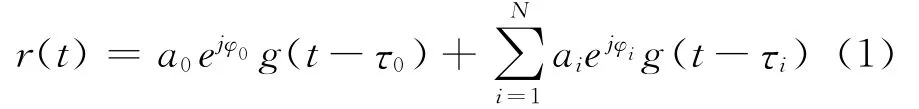
式中，g（t）为信号发射时的复包络，a0、φ0、τ0分别为直射信号的幅度、相位和传播时延，ai、φi、τi为第i路多径信号的幅度、相位和传播时延，N为多径信号的个数。为简化讨论，考虑单个多径情形，即N＝1。

多径影响主要表现在对实际接收多径和直视合成信号相关特性的影响［5］。当直视信号幅度为1，反射多径信号的幅度为0.5，多径延迟为0.4 chip时，合成信号的相关特性如图1所示。

实际信号的接收过程中，多径信号相对直射信号的相对相位和幅度不断变化，引起码环鉴别器偏离平衡跟踪点，从而产生伪码跟踪误差［6］。码环一般选择相干超前减滞后延迟锁定环，其码环鉴别器的多径误差包络输出为

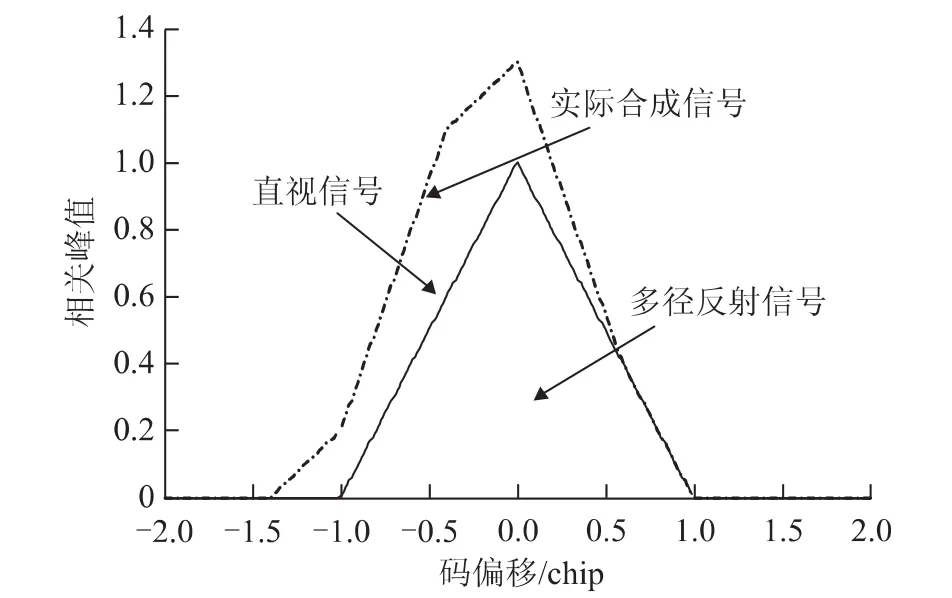
图1 合成信号相关特性

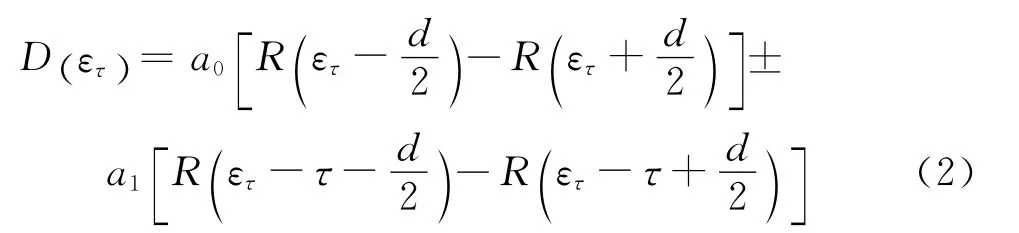
式中，R（τ）为码相关函数，ετ为直达信号时延误差估计，τ为多径时延，d为超前滞后相关器间距。鉴别器输出为零时的ετ值即为多径误差，也就是求以下方程的解

对D（ετ） 在0点附近进行一阶泰勒展开得

考虑信号带宽时，码相关函数和功率谱密度的关系为

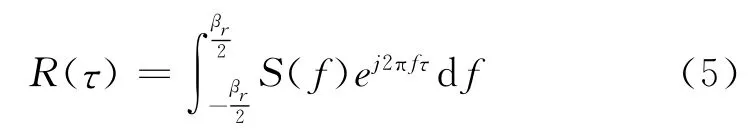
式中，βr为信号带宽，S（f）为信号功率谱密度。结合式（2）、式（3）、式（4）及式（5）可得到多径误差的最终输出为

基于式（6），生成了不同信号带宽、不同信号间距下的多径误差包络，结果如图2所示。

由图2结果可以看出，多径误差和信号带宽和相关间距有关，当信号带宽较小时，仅靠减小相关间距的抗多径效果有限，窄相关技术在信号带宽较宽时抗多径效果明显［7］。北斗系统B1频点码速率为2.046MHz，B3频点码速率为10.023MHz，B3频点信号带宽约为B1频点5倍，从仿真结果可以看出，B3频点相对B1频点信号具有更好的抗多径性能。

图2 不同信号带宽、不同相关间距时的多径误差包络

3 仿真数据分析

利用信号源模拟两颗卫星信号。其中一通道模拟1号卫星伪距，不叠加多径信息，作为参考信号；二通道模拟2号卫星，和1号卫星放置在同一位置；同时利用第三通道模拟2号卫星的一路多径信号，多径信号幅度为直射信号的0.5，多径信号延迟从0开始，以0.01m/s的速率递增，逐渐增大至1.5chip。

北斗接收机跟踪测量1号卫星和2号卫星的伪距观测值，其中2号卫星伪距将受到多路径的影响。

采用华力创通公司信号源生成仿真数据，利用不同厂家接收机，以有线方式进行数据采集。

将2号卫星伪距减去1号卫星伪距，即可获得不同时刻不同多路径影响下的伪距测量误差，进而生成多路径误差包络图，分析已知多径大小情况下对接收机伪距测量精度影响。

分别基于北斗系统B1频点和B3频点I支路伪距进行仿真测试，结果如图3～图8所示。

（1）B1频点伪距多径仿真测试结果

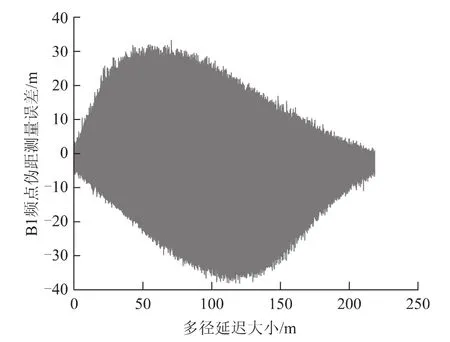
图3 A公司B1频点伪距多径仿真测试结果

图4 B公司B1频点伪距多径仿真测试结果

图5 C公司B1频点伪距多径仿真测试结果

（2）B3频点伪距多径仿真测试结果

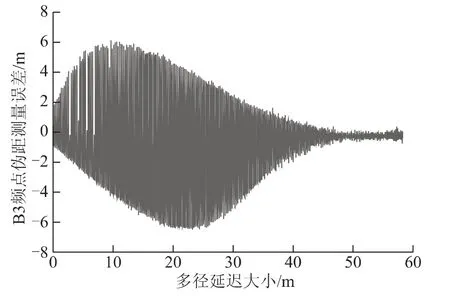
图6 A公司B3频点伪距多径仿真测试结果

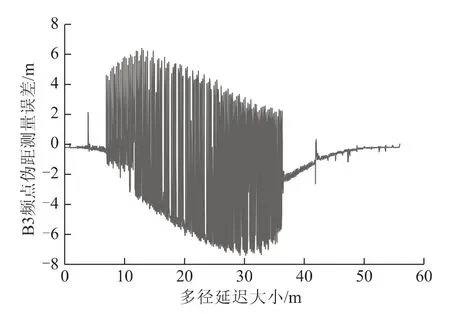
图7 B公司B3频点伪距多径仿真测试结果

图3～图8中，横坐标表示模拟多径延迟量，纵坐标表示伪距多径误差。从结果可以看出：

图8 C公司B3频点伪距多径仿真测试结果

（1）伪距多径大小和信号带宽相关。B1频点带宽较窄，受多径影响较大；B3频点带宽较宽，受多径影响相对较小。

（2）不同厂家接收机受多径影响大小不同，可能和接收机基带算法和相关间距有关；C公司接收机相关间距较小，能够显著减小B3频点伪距多径影响。

（3）与仿真多径大小相比，接收机观测到的所有伪距多径均有不同程度减小，说明北斗用户机对多径有一定的抑制作用。

4 实测数据分析

基于北斗民用导航型接收机实测数据，本文设计了短基线差分方法。首先，利用两个观测站组成双差观测方程［8］（消除了卫星钟差、接收机钟差、电离层延迟、对流层延迟和硬件延迟偏差），并代入两个观测站的精确坐标；其次，基于双差观测方程和误差传播规律，分离出单差观测方程，则该单差方程残差中仅包含伪距多径和噪声影响，根据误差传播定律，上述单差伪距多径和噪声除以，即可得到非差伪距多径和噪声大小。短基线差分方法已完全消除硬件延迟等各类误差［9－10］，更直观地反映伪距多径和噪声大小。

数据来源为北京测站的两台导航型接收机，两台接收机分别放置在间隔34m的两个已知点上，都设置为B1和B3双频定位模式，记录原始伪距及导航电文信息。数据采集时间为2012－08－27T06—28 T 06－20，大约24h，高度截止角5°，采样间隔1s。

部分可见卫星B1频点和B3频点伪距差分残差结果如下图所示，图中上半部分为残差大小，下半部分为卫星高度角。

图9～图14中，横坐标表示时间（北斗时周内秒），纵坐标分别表示伪距多径残差大小（m）和卫星高度角（°）。从图中统计结果可以看出：

图9 C05卫星B1频点伪距多径误差

图10 C05卫星B3频点伪距多径误差

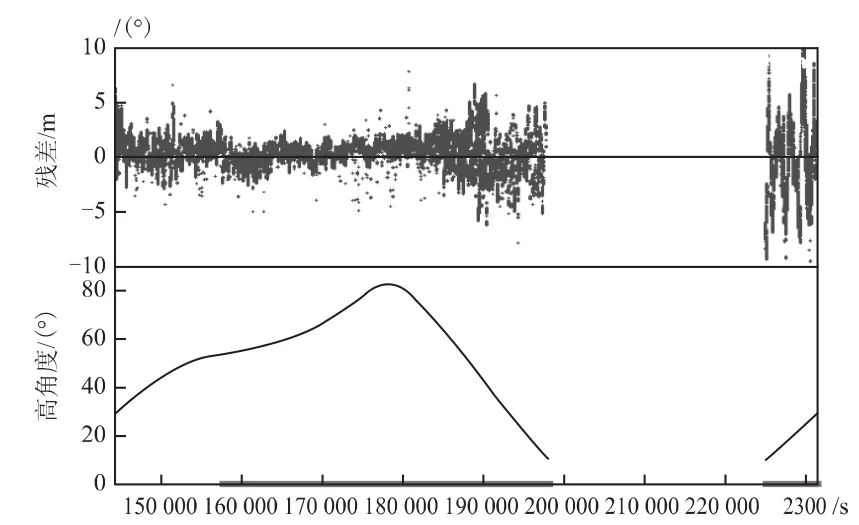
图11 C10卫星B1频点伪距多径误差

图12 C10卫星B3频点伪距多径误差

图13 C12卫星B1频点伪距多径误差

（1）BDS伪距多径大小和卫星类型相关，GEO卫星受伪距多径影响比IGSO卫星和MEO卫星大，B1频点多径误差均方根（root mean square，RMS）最大达2.35m，B3频点RMS最大达0.73m。

（2）伪距多径影响大小和频点相关，所有卫星均为B1频点受多径影响较B3频点大，主要原因为B1频点带宽较小，易受多径误差影响。

图14 C12卫星B3频点伪距多径误差

5 结论

基于BDS信号体制及星座特点，本文详细分析了北斗系统伪距多径特性及对定位性能的影响，首次对不同厂家北斗接收机的抗多径性能进行了仿真测试，结论如下：

（1）北斗系统B1频点伪距多径大于B3频点，主要原因为B1频点带宽较小，易受多径误差影响。

（2）GEO卫星受伪距多径影响比IGSO卫星和MEO卫星大，GEO卫星B1频点RMS最大达2.35m，B3频点RMS最大达0.73m。

（3）在信号带宽较宽情况下，窄相关技术可以有效抑制多径误差，仿真结果表明，北斗接收机采用窄相关技术后B3频点伪距多径显著减小。

［1］许其凤.GPS卫星导航与精密定位［M］.北京：解放军出版社，1994：12－25.

［2］刘荟萃，程肖，倪少杰，等.一种基于误差包络的多径抑制性能评估准则［J］.国防科技大学学报，2011，33（1）：72－75.

［3］李豹，许江宁，曹可劲，等，北斗二代导航信号抗多径性能分析与仿真［J］.中国惯性技术学报，2012，20（3）：339－342.

［4］SENNOTT J W，PIETRASZEWSKI D.Experimental Measurement and Characterization of Ionospheric and Multipath Errors in Differential GPS［J］.Navigation，1987，34（2）：160－173.

［5］张孟阳，吕保雄，宋文森.GPS系统中的多径效应分析［J］.电子学报，1998，26（3）：10－14.

［6］GOLDHIRSH J，VOGEL W J.Mobile Satellite System Fade Statistics for Shadowing and Multipath from Roadside Trace at UHF and L－band［J］.IEEE Transactions on Antennas and Propagation，1989，37（4）：489－498.

［7］MCGRAW G A，BRAASCH M S.GNSS Multipath Mitigation Using Gated and High Resolution Correlator Concepts［C］//Proceedings of the 1999National Technical Meeting of The Institute of Navigation.San Diego：［s.n.］，1999：333－342.

［8］魏子卿，葛茂荣.GPS相对定位的数学模型［M］.北京：测绘出版社，1998：33－62.

［9］LACHAPELLE G，FALKENBERG B，NEUFELDT D，et al.Marine DGPS Using Code and Carrier in a Multipath Environment［C］//Proceedings of the Second International Technical Meeting of the Satellite Division of the ION：ION’S Satellite Division.Colorado：［s.n.］，1989：26－29.

［10］李征航，黄劲松.GPS测量与数据处理［M］.北京：测绘出版社，2005.