Damping of Oblique Ocean Waves by a Vertical Porous Structure Placed on a Multi-step Bottom

Santu Das and Swaroop Nandan Bora

Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati-781039, India

Damping of Oblique Ocean Waves by a Vertical Porous Structure Placed on a Multi-step Bottom

Santu Das and Swaroop Nandan Bora＊

Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati-781039, India

Oblique ocean wave damping by a vertical porous structure placed on a multi-step bottom topography is studied with the help of linear water wave theory. Some portion of the oblique wave, incident on the porous structure, gets reflected by the multi-step bottom and the porous structure, and the rest propagates into the water medium following the porous structure. Two cases are considered: first a solid vertical wall placed at a finite distance from the porous structure in the water medium following the porous structure and then a special case of an unbounded water medium following the porous structure. In both cases, boundary value problems are set up in three different media, the first medium being water, the second medium being the porous structure consisting of p vertical regions-one above each step and the third medium being water again. By using the matching conditions along the virtualvertical boundaries, a system of linear equations is deduced. The behavior of the reflection coefficient and the dimensionless amplitude of the transmitted progressive wave due to different relevant parameters are studied. Energy loss due to the propagation of oblique water wave through the porous structure is also carried out. The effects of various parameters, such as number of evanescent modes, porosity, friction factor, structure width, number of steps and angle of incidence, on the reflection coefficient and the dimensionless amplitude of the transmitted wave are studied graphically for both cases. Number of evanescent modes merely affects the scattering phenomenon. But higher values of porosity show relatively lower reflection than that for lower porosity. Oscillation in the reflection coefficient is observed for lower values of friction factor but it disappears with an increase in the value of friction factor. Amplitude of the transmitted progressive wave is independent of the porosity of the structure. But lower value of friction factor causes higher transmission. The investigation is then carried out for the second case, i.e., when the wall is absent. The significant difference between the two cases considered here is that the reflection due to a thin porous structure is very high when the solid wall exists as compared to the case when no wall is present. Energy loss due to different porosity, friction factor, structure width and angle of incidence is also examined. Validity of our model is ascertained by matching it with an available one.

porous structure; oblique wave; reflection; matching condition; multi-step bottom; friction factor; energy loss

1 Introduction

The concept of porous media is used in many areas of applied science and engineering: filtration, mechanics (acoustics, geomechanics, soil mechanics, rock mechanics (Xi et al., 2011)), engineering (petroleum engineering, bioremediation (Anglin et al., 2008), construction engineering), geosciences (hydrogeology, petroleum geology (Blunt, 1998), geophysics), biology, biophysics (Clement et al., 1996), material science, etc. These works amply justify that fluid flow through porous media is a subject of immense common interest and has, hence, emerged as a separate field of study. In coastal areas, porous structures are widely used as breakwaters to protect harbors, inlets and beaches from wave action, and as dissipating sea-walls to attenuate the wave energy in harbors. Because of this immense significance of porous structures interacting with ocean waves, we are motivated to investigate some specific cases of reflection by a porous structure.

Many aspects of interaction between waves and porous media have been studied extensively. Theoretical solutions for reflection and transmission coefficients for certain type of porous structures have been analyzed previously by a number of researchers. The most widely used model of wave-induced flow in porous medium is the one developed by Sollitt and Cross (1972). According to this approach, dissipation of wave energy inside a porous medium is taken into account through a linearized friction term f which is evaluated by an iterative procedure. Madsen (1974) derived a simple solution for reflection and transmission from a rectangular porous structure under normal incidence of long waves based on the linearized form of the governing equations and also that of the flow resistance formula. Madsen (1983) obtained a theoretical solution for the reflection of linear shallow-water waves from a vertical porous wave absorber placed on a horizontal bottom. The friction term describing the energy loss inside the absorber was linearized and thereafter, by using Lorentz principle of equivalent work, the reflection coefficient was determined as a function of parameters describing the incoming waves and the absorber characteristics. Kirby and Dalrymple (1983) investigated the diffraction of obliquely incident surface waves by an asymmetric trench in which they developed a numerical solution by matching the particular solution foreach sub region of constant depth along the vertical boundaries. An approximate solution based on plane-wave modes was derived and compared with the numerical solution. Sulisz (1985) formulated a theory to predict wave reflection and transmission at an infinite rubble-mound breakwater under normal wave incidence. Dalrymple et al. (1991) adopted the approach of Sollitt and Cross (1972) to analyze the reflection and transmission of oblique incident waves from infinitely long porous structures. Losada et al. (1993) extended this study to the case of an infinitely long, homogeneous, vertical structure capped with an impervious element under oblique incident wave. Mallayachari and Sundar (1994) took into account the effects of an uneven sea-bed. The variation of the reflection coefficient with the porosity of the wall, its friction factor and the relative wall width was studied. Zhu (2001) used wave induced refraction-diffraction equations for surface waves in the region occupied by a porous structure. He used the orthogonality of the depth-dependent functions. Zhu and Chwang (2001) also extended theearlier study of Zhu (2001) by considering a water chamber behind the porous structure and they concluded that with a proper choice of the geometry and the hydraulic characteristics of the composite wave absorber with a water chamber, reflection can be reduced considerably. Liu et al. (2008) examined the hydrodynamic performance of a modified two-layer horizontal-plate breakwater consisting of an upper submerged horizontal porous plate and a lower submerged horizontal solid plate. Liu and Li (2011) extended this work by considering a double curtain-wall breakwater whose seaward wall was perforated and shoreward wall impermeable. Cho et al. (2013) further extended the idea of Liu et al. (2008) by considering the lower submerged horizontal plate as a porous one instead of an impermeable one. Das and Bora (2014a) investigated wave reflection by a rectangular porous structure placed on an elevated bottom and supported by a vertical wall. The variation of reflection with respect to the number of modes, porosity, structure width etc., was studied. Das and Bora (2014b) also studied wave damping by a vertical rectangular porous structure placed near and away from a rigid vertical wall. They computed the reflection coefficients for various depths, structure width and porosity. An extension of this work was carried out by Das and Bora (2014c) by placing the porous structure on a multi-step horizontal bottom. A special case by removing the rigid wall was also investigated.

The objective of this work is to solve water wave scattering problems due to the presence of a porous structure placed on a p-step horizontal bottom followed by a water region bounded by a rigid vertical wall placed at a distance from the porous structure and study the reflection coefficient and the dimensionless amplitude of the transmitted progressive wave. The effects of various parameters, such as number of evanescent modes, depth, porosity, friction factor, structure width and angle of incidence on the reflection coefficient and the dimensionless amplitude of the transmitted progressive wave are studied and the results are presented graphically. To the best of the authors’ knowledge, no one has solved oblique ocean wave damping through a porous structure which is placed on a multi-step horizontal bottom. A special case of an unbounded water region following the porous structure placed on the p-step horizontal bottom is considered and the reflection coefficient and the dimensionless amplitude of the transmitted progressive wave for the various set of parameters, as mentioned earlier, are studied as was done for the former case.

2 Mathematical formulation

Though the present problem is a specific one involving a vertical porous structure, it is fairly important to discuss some general features and equations which usually arise in wave propagation in porous medium. Therefore, in the following subsections a brief description on the specific porous structure under consideration is presented along with these equations ahead of the formulation of the present problem.

2.1 Porosity and porous structure

A porous medium mostly consists of pores through which fluid (be it gas or liquid such as water) can pass. The skeleton part of the medium is mainly solid (but foam is considered to be porous though). A porous medium may be an aggregate of alarge number of particles like sand, gravels or a solid containing many capillaries such as porous rock. Many natural substances like sponge, soil, biological materials (bone, lungs etc.) are some examples of porous material.

Fig. 1 Front view of the structural model

There are many man-made porous materials such as cement, ceramics etc. Depending upon the pore size, porous structures can be categorized into three types, namely, microporous (smaller than 2 nanometers), mesoporous (between 2 and 50 nanometers) and macroporous (larger than 50 nanometers). Metallic foams are good examples of porous materials with higher porosity (ranging from 0.6 to 0.96). The construction of these types of materials can be accomplished through many means–the main one being the‘lost-foam casting’. Porous structures, with high porosity but with considerable stability, to be used as breakwater inocean and coastal engineering, can be constructed from low melting metals and alloys such as copper, aluminum, lead, tin, zinc, etc. The porous structure under consideration in this manuscript is taken as such a type of structure. Fig. 1 presents a rough visual representation of the present structural model.

2.2 General theory for flow inside porous medium

Small amplitude wave motion is considered within an undeformable porous medium. It is assumed that the porous structure is homogeneous and isotropic. The fluid motion follows the continuity equation and the equation of motion in terms of the seepage fluid velocity U and dynamic pressure P which are given by

whereρ is the density of the fluid, f is the linearized friction factor and ω is the angular frequency of the incident wave.

The inertial coefficient S is defined by

whereMC is the added mass coefficient and γis the porosity of the porous structure. The physical significance and derivation of Eqs. (1a), (1b) and (2) are described in Appendix A.

A pore velocity potential Φ(x,y,z,t )is introduced to describe the wave-induced fluid motion in the porous medium:

Integration of equation of motion (1b) leads to Bernoulli’s equation

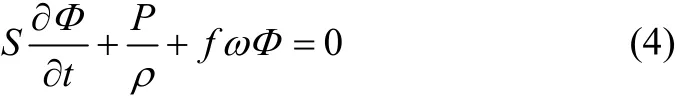
The potential Φ is assumed to be harmonic in time. So the fluid velocity, dynamic pressure and velocity potential can, respectively, be written as

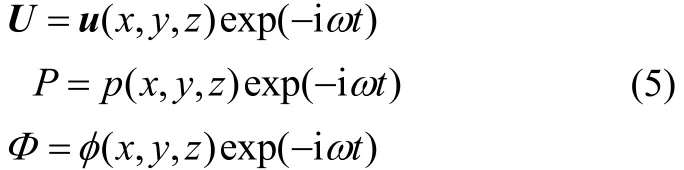
where u, p and φare spatial functions independent of time. Substitution of these values into Eqs. (1a), (1b) and (3) leads to the equations

where α=f-iS is the dimensionless impedance of the porous medium. Using Eq. (6a) in Eq. (6c), the spatially dependent potential function φ satisfies Laplace’s equation

If the free surface is defined by z=η(x,y,t), then the linearized dynamic free surface boundary condition can be obtained from (4) with P gρη= as

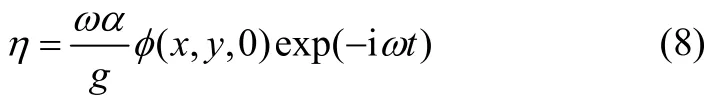
The linearized kinematic free surface boundary condition can be written as

Combining (8) and (9), the following single free surface condition is obtained:

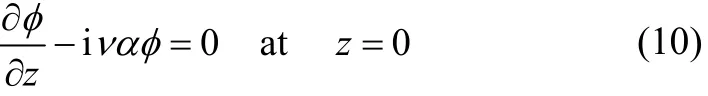
with g as the gravitational constant. The condition at the impermeable bottom is

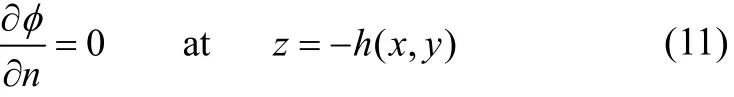
For a flat sea-bed at z h=- when h is constant, the general solution of the two-dimensional wave motion within a porous medium can be obtained as follows by solving Eqs. (7)–(11) for the potential in x and z with the help of the technique of separation of variables:

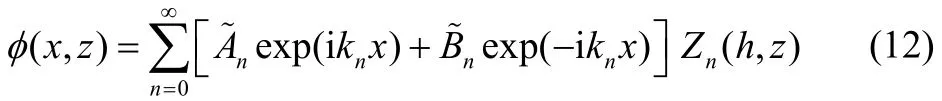
with the complex wave numbernk satisfying the complex dispersion relation

The characteristics of waves in the porous medium can be described by the dimensionless complex wave numbernkh. It is known that for a non-dissipative mediumis purely real, whileare purely imaginary. For a dissipative medium, it is noted that the influence of the friction factor f is to damp the wave motion. This damping can be achieved by adding an imaginary part to0k and real parts to. Subsequently, the amplitudes of both propagating mode and evanescent mode will decay.

2.3 Formulation

Let us consider a vertical porous structure of width L along the mean free surface, placed on a p-step bottom topography above the horizontal ocean bottom, which is at a constant depth1h from the free surface. Using Cartesiancoordinate system, the positive x-direction is defined as the direction of the wave incident on the porous structure at x=0, the positive z-direction considered vertically upwards and the mean free surface as 0z= . Due to the p-step bottom topography under the porous structure, p different heights of the porous structure exist, namely,jh whenfor each j=2, 3,…, p+1 where

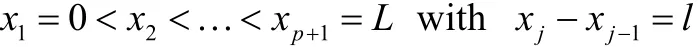
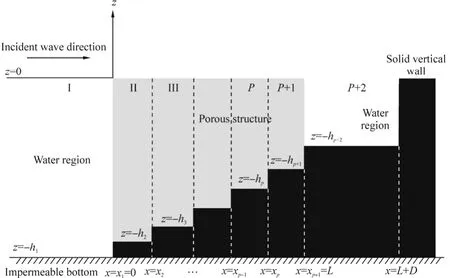
Fig. 2 Schematic diagram of the problem with rigid vertical wall

The governing equation and the boundary conditions in region Iare

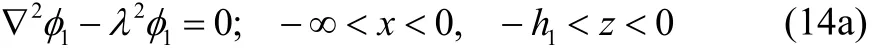
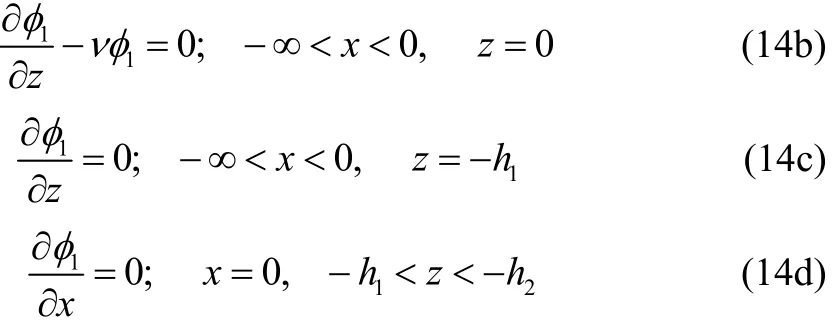
The governing equation and the boundary conditions in region j ( j=2, 3,…, p+1) are

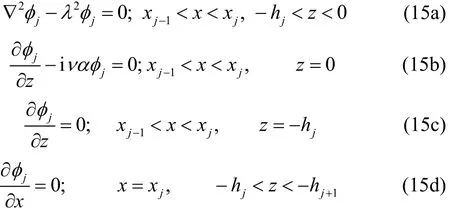
The governing equation and the boundary conditions in regionare

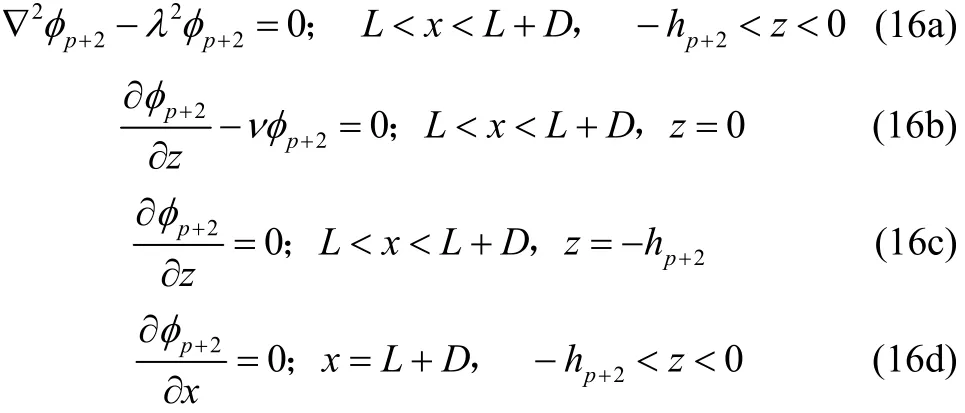
In addition to the governing equations and different boundary conditions for each region, there exist some other conditions, called matching conditions, along the common boundary of any two successive media. These conditions imply the continuity of pressure and mass flux across the boundaries. The matching conditions along the boundariesandare given by

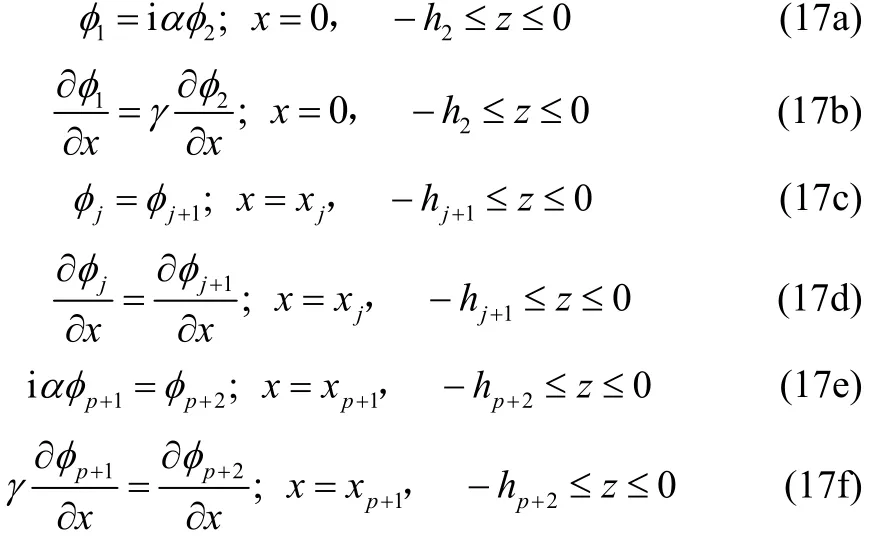
Derivation of the matching conditions (17a–f) is detailed in Appendix B.

2.4 Reflection and transmission by the porous structure

The velocity potential1(,)xzφ in region I is given by the following form:

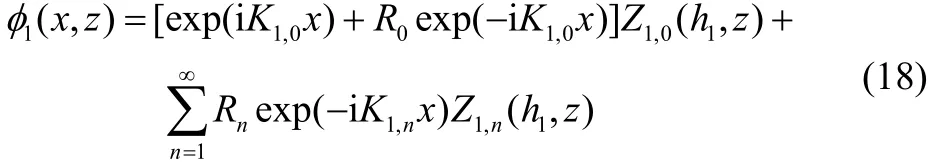
where0R is the complex reflection coefficient,nR correspond to the decaying modes of reflection; and the depth-dependent functionandare, respectively, given by

Eq. (19c) has one positive real root1,0k corresponding to the incident and reflected modes of wave propagation, and infinitely many purely imaginary roots1,nk ; 1,2,n …= , which correspond to the evanescent modes. We truncate the infinite sum at n=N so as to consider a finite number of evanescent modes N only:

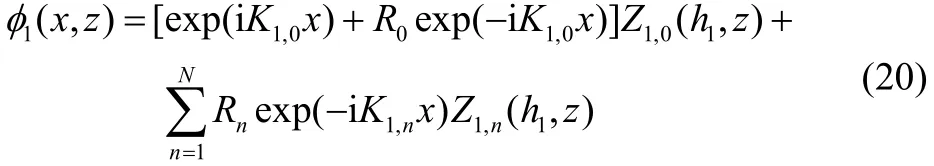
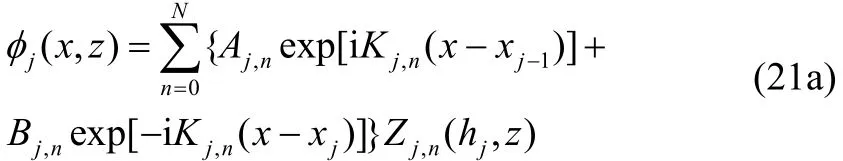
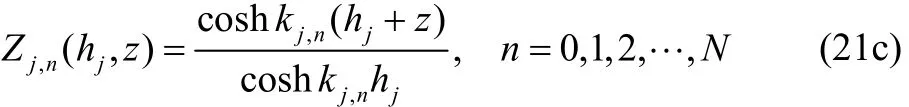
In region p+2 (L＜x＜L+D, −hp+2＜z＜0), the horizontal impermeable bottom is considered at. Hence, the integrals in the porous region must be fromto z=0 in order to meet the matching conditions and it is required to compute the relevant integrals fromto z=0. The velocity potentialafter truncating the infinite sum at n=N, can be written as

where0C is the dimensionless amplitude of the transmitted progressive wave, Cn(n=1, 2,…,N) and Dn(n=1, 2,…,N) are arbitrary constants;withsatisfying the dispersion relation And

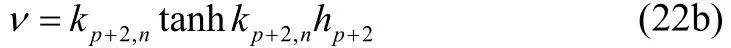
is the depth-dependent function given by

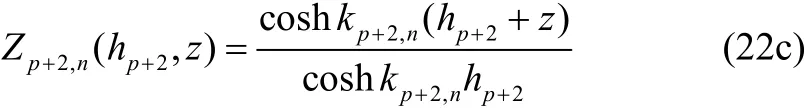
Further, using (16d),2pφ+can be reduced to the following form:

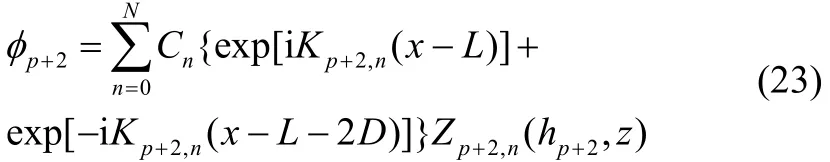
When the energy loss during the whole process of scattering is discussed, the following definition is tobe used:

Using the matching conditions (17a, 17b) along the boundary, we get

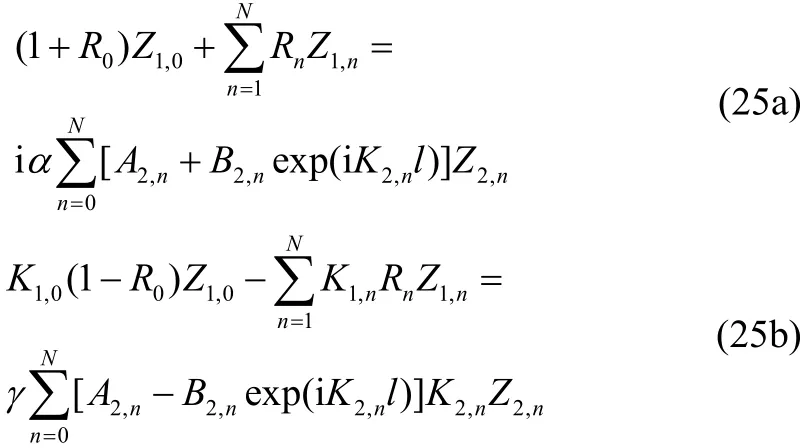
Further, using the matching conditions (17c, 17d) along the boundaryit follows

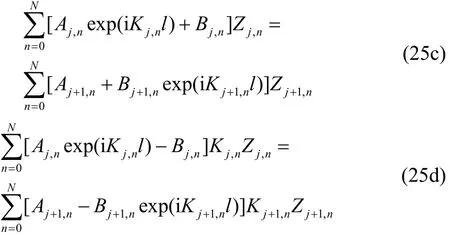
Applying the matching conditions (17e, 17f) along the boundary, we obtain

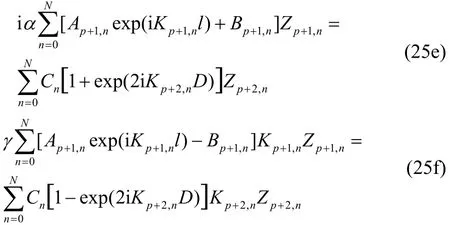
Further, using the orthogonality property of(j=2, 3,…, p) andfor each m=0, 1,…,N, in (25a, 25b), (25c, 25d) and (25e, 25f), respectively, we have

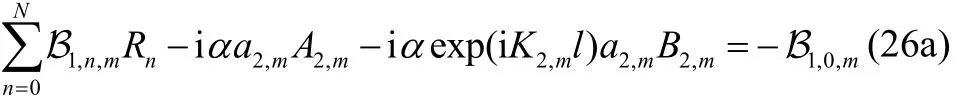
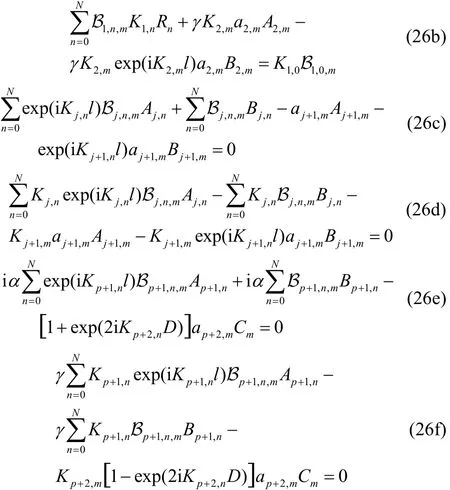
where

Eqs. (26a)–(26f) reduce to the following system:

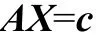
where A is a square matrix of size 2(p+1)(N+1),

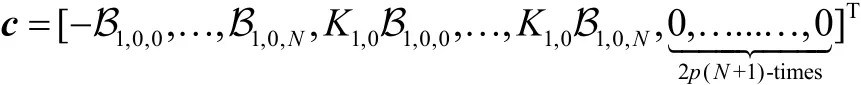
is the unknown vector, and By solving the above system of linear equations,andcan be evaluated and subsequently the overall scattering phenomenon by the porous structure can be discussed.

3 Numerical results

Results are shown for variation in the reflection coefficientand the dimensionless amplitude of the transmitted progressive waveagainst the dimensionless width of the porous structure (L/h1) as well as the angle of incidence (θ) for various parameters such as the number of evanescent modes (N), porosity（γ） , friction factor (f) and number of steps (p). Energy loss curves are also plotted against (L/h1) and θ. For computational purpose, some constant values for different parameters are considered:N=10, γ=0.9, f=1 and p=7. Throughout the computation, the dimensionless wave numberis considered fixed at

In order to study the effect of the number of evanescent modes on scattering characteristics,andare plotted against L/h1in Fig. 3 by keeping all other parameters constant. Fig. 3(a) shows large values offor relatively small value of L/h1, suggesting that in order to get lower reflection, thin porous structure needs to be avoided. It is noted that around L/h1=1.25, the reflection coefficient attains a minimum value and then increases with an increase in the value of L/h1before stabilizing at a fixed value ofThe minimum value may occur due to the cancelation of reflection from the step bottom as well as the rigid vertical wall and vertical front face of the porous structure (Straub et al., 1957). It is also found that the reflection characteristic is independent of the number of evanescent modes. Now large transmission is found to take place for relatively lower value of L/h1(Fig. 3(b)). Further increase in L/h1results in decrease ofand it approaches zero. The behavior ofis also independent of the number of evanescent modes.

The effect of different values of porosity on scattering phenomenon is studied by plottingandagainst L/h1(Fig. 4). From Fig. 4(a), it is observed that in each curve, as the dimensionless width of the structure is increased,initially decreases rapidly, attains a minimum value and again increases slightly before obtaining a constant value. It is notable that higher value of porosity gives rise to lowerthe occurrence of which is as per expectation. Fig. 4(b) suggests thatis independent of the value of the porosity considered. It is observed that higher values ofoccur for a thin porous structure but with an increase in L/h1,decreases rapidlybefore converging to zero.

Fig. 3 Effect of dimensionless width of the porous structure L/h1for different numbers of evanescent modes N with υh1=0.8, D/h1=10, θ=0°, γ=0.9, f=1 and p=7

Fig. 4 Effect of dimensionless width of the porous structure L/h1for different γ with υh1=0.8, D/h1=10, θ=0°, N=10, f=1 and p=7

Fig. 5 Effect of dimensionless width of the porous structure L/h1for different f with υh1=0.8, D/h1=10, θ=0°, N=10, γ=0.9, and p=7

Fig. 6 Effect of dimensionless width of the porous structure L/h1for different p with υh1=0.8, D/h1=10, θ=0°, N=10, γ=0.9 and f=1

We observe in Figs. 3–6 that reflection and transmission are very high when the porous structure is very thin. When the width of the porous structure is almost zero, i.e., no porous structure is present, total transmission takes place and hence the amplitude of incoming wave is same as the amplitude of the transmitted wave.

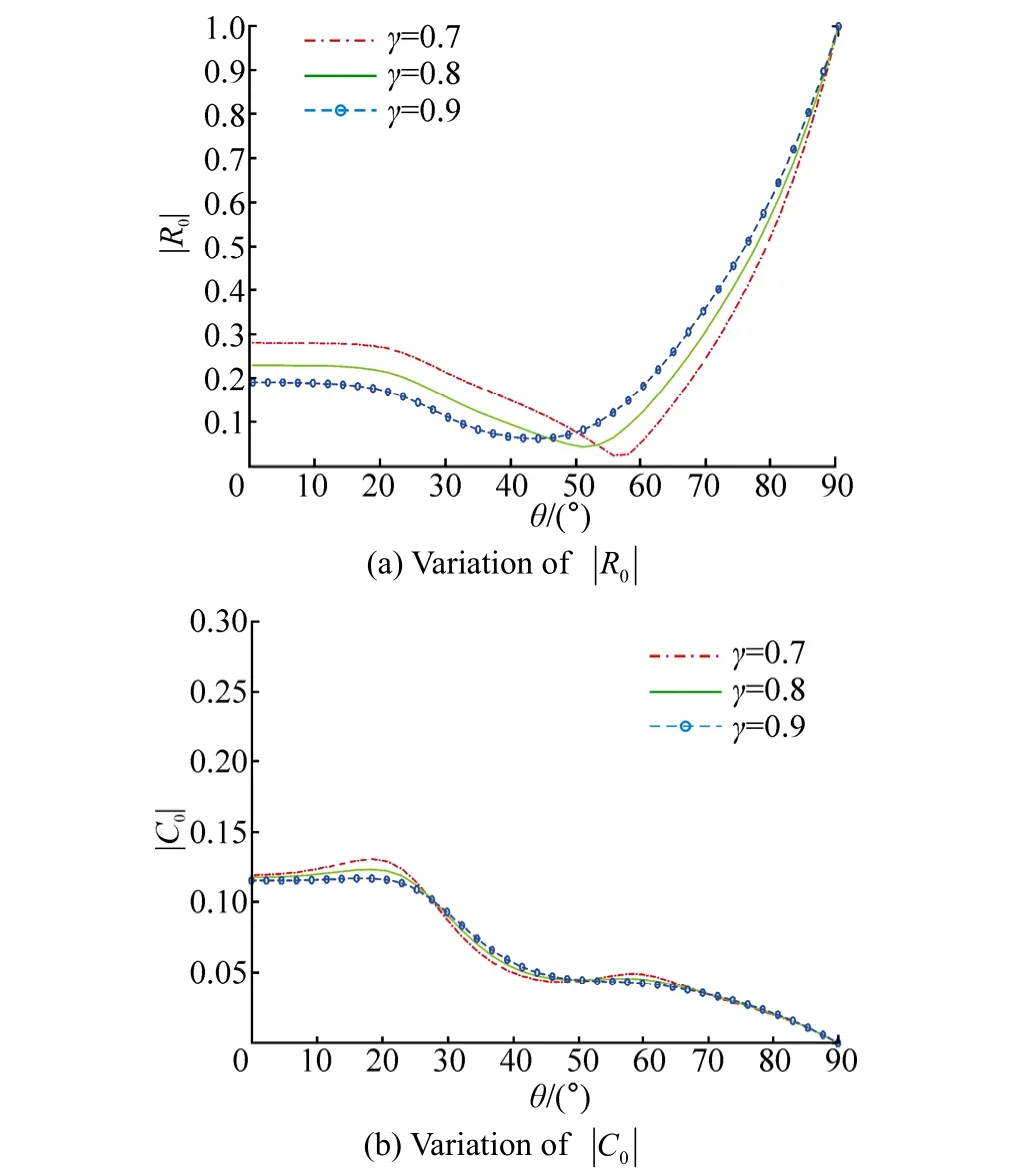
Fig. 7 Effect of angle of incidence θ for different γ with υh1=0.8, D/h1=10, L/h1=3, N=10, f=1 and p=7

Fig. 8 Effect of angle of incidence θ for different γ with υh1=0.8, D/h1=10, L/h1=3, N=10, γ=0.9 and p=7

We also observe that the left propagating mode arising from the solid wall placed at x L D= + has the same magnitude as that of the transmitted wave. This left propagating mode is responsible for reflection taking place (virtually) at x = 0. Thereforein this case. This is the reason why both the reflection and transmission are very high when 0L→ .

In Fig. 8, the effect of incident wave angle on scattering characteristics is studied for different values of friction factor. Fig. 8(a) shows the variation of for different values of f. Oscillation is observed for lower values of frictionfactor ( f= 0.25) which disappears if higher value of friction factor ( f= 1) is considered. Convergence ofis observed for higher values of friction factor. Variation infor different values of f is shown in Fig. 8(b). The higher the value of θ, the lower is the valuetakes before converging to zero. It is found that up to 40θ= °(approx.),is higher for lower value of f considered. Afterwards the above mentioned property reverses but the difference in their values is very small compared to those for

3.1 Energy loss

The energy loss of the wave incident on the porous structure is discussed graphically in Figs. 9–10.

Fig. 9 Energy loss (%) against dimensionless width of the porous structure (L/h1) with υh1=0.8, D/h1=10, θ=0°, N=10 and p=7

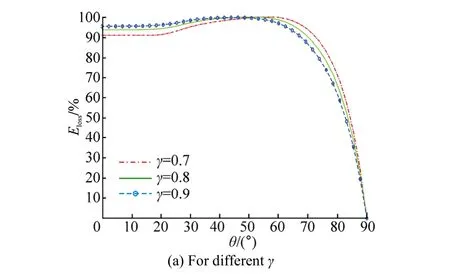
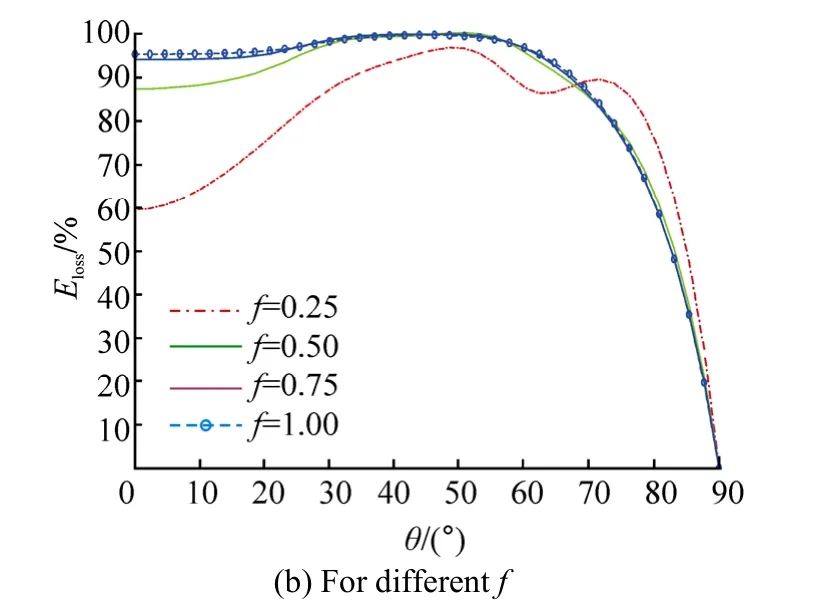
Fig. 10 Energy loss (%) against angle of incidence θ with υh1=0.8, D/h1=10, L/h1=3, N=10 and p=7

Fig. 9 depicts the energy lossagainstfor different values of porosity and friction factor. Steep portion of the energy loss curve in Fig. 9(a) suggests the admissible width of the porous structure in order to be an effective wave absorber. Further increase inresults in obtaining a constant value of energy loss. This characteristic is observed for all the values of porosity taken. It is also found that higher porosity causes higher energy loss compared to lower values of porosity. On the other hand, minimum admissible width of the porous structure varies for different values of f–larger admissible width of the porous structure is required for lower values of f as compared to the higher values of f. It is noticeable that higher f results in higher energy loss but converges ultimately for larger width of the structure.

The effect of θ on scattering phenomenon for different values of porosity and friction factor is studied graphically from Fig. 10. Energy loss is very high for different values of porosity considered (Fig. 10(a)). But steep descent in the energy loss curves is observed for large values of θ before converging to zero. It is observed that energy loss is higher for higher values of porosity when 50θ＜ ° (approx.). Beyond that range of θ, the curves cross each other and the characteristic reverses. Convergence in energy loss curves is found for higher values of friction factor taken (Fig. 10(b)). Maximum energy loss occurs in 40 50θ＜ ＜° °, irrespective of the value of f. When 0θ= , i.e., for normal incidence, energy loss is much higher for 1f= than that for f=0.25, but increases rapidly for 0.25f= as θ increases. Oscillation in the energy loss curve is also found corresponding to 0.25f= .

3.2 Comparison with existing result

In order to ascertain that our model is effective, we compare our reflection coefficients plotted against the dimensionless porous structure widthwith those from the work of Madsen (1974). This is accomplished by taking, i.e., by placing the porous structure on thehorizontal sea-bed instead of a p-step bottom. Excellent agreement between our result and Madsen’s result can be observed from Fig. 11. This confirms that our model is valid and hence can be employed effectively to investigate various issues related to scattering of waves by a porous structure placed on a p-step bottom.

Fig. 11 Variation of reflection coefficientagainst dimensionless width of porous structure (k1,0L) for different porosity (γ) with steps=40, h1=21, hp+1=h1, D=0, f=1, δ=0.2, T=17.3, ai=0.87 and N=10 (Comparison with Madsen (1983))

4 Special case: unbounded (p+2)thregion

In this case, the formulation of the problem is same as that of the previous one except for the last region where no solid wall is placed, i.e., the last region is unbounded (Fig. 12). Potential functionsjφ , depth dependent functionsandin region j (j=1, 2,…, p+1) satisfy the forms as described earlier. The only difference occurs in the potential functionin regionwhich, after truncating the infinite sum at n N= , can be written in the following form:

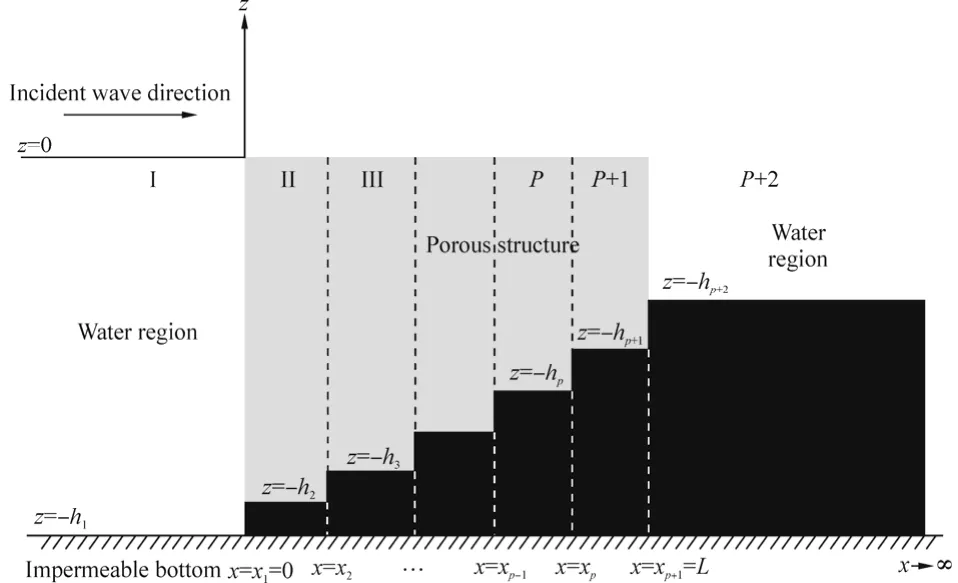
Fig. 12 Schematic diagram of the problem of particular case in unbounded region

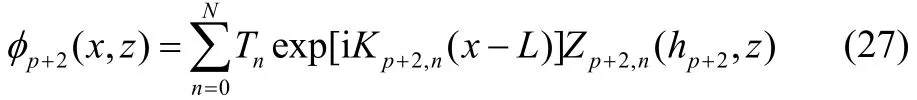
where0T is the transmission coefficient,nT (n=1, 2,…,N) are arbitrary constants,satisfies Eq. (22c) andwithsatisfying Eq. (22b). It is to be noted that now transmission coefficient appears inbecause of the consideration of an infinite fluid domain.

By applying the same technique adopted earlier, the following system of linear equations is obtained:

A matrix system can be constructed as per our earlier discussion and subsequently the scattering phenomenon can be discussed.

4.1 Numerical results

Here also the same study is carried out as was done in the previous case, with the same set of constant parameter values.

Fig. 13 depicts the variation ofandagainst L/h1for different numbers of evanescent modes. Bothandare independent of N and follow the same pattern as observed in Fig. 3. But the difference occurs in(Fig. 13(a)) where for a thin porous structure, the value ofis quite small and the minimum value occurs at a smaller value of1/L h compared to that in Fig. 3(a).

The effect of porosity on scattering process is shown in Fig. 14. Reflection characteristic (Fig. 14(a)) is same as described in Fig. 4(a) except for the fact that the value ofis small for small values of L/h1as compared to that in Fig. 4(a). Fig. 14(b) describes the effect of1/L h onfor different values of porosity. The nature of the curves is very similar to that in Fig. 4(b).

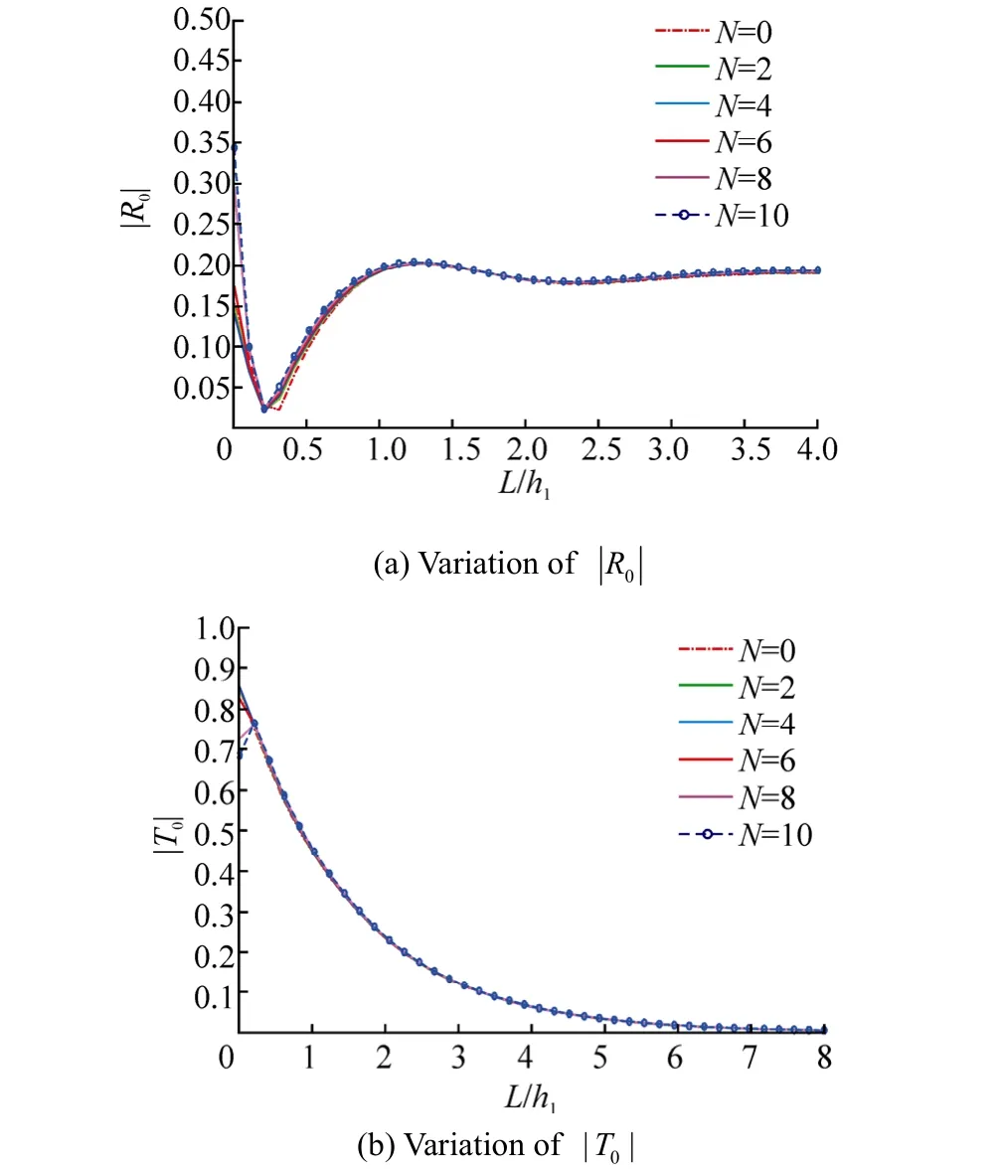
Fig. 13 Effect of dimensionless width of the porous structure L/h1for different numbers of evanescent modes (N) with υh1=0.8, θ=0°, γ=0.9, f=1 and p=7

Fig. 14 Effect of dimensionless width of the porous structure L/h1for different γ withυh1=0.8, θ=0°, N=10, f=1 and p=7

Further Fig. 15 shows the variation ofandagainst L/h1for different values of friction factor. Small value of friction factor (f=0.25)results in oscillation in the value ofwhich disappears with an increase in the value of friction factor (Fig. 15(a)). Moreover, higher friction factor gives rise to higher reflection except for a thin width of the porous structure. The nature of transmission (Fig. 15(b)) is same as described in Fig. 5(b).

The effect of number of steps on variation ofandis shown in Fig. 16. In Fig. 16(a), steep verticalportion of the curve for p=3 defines the minimum admissible width of the porous structure. Convergence of the curves for higher values of pis observed from the graph. is very high for a thin porous structure (Fig. 16 (b)) for all the values of p and decreases with the increase in the value of L/h1before vanishing for large value of L/h1.

Fig. 17 demonstrates scattering against the angle of incidence for different values of porosity. The nature of the curves is very similar to that discussed in Fig. 7.

Moreover, the study of scattering characteristics against θ for different values of friction factor is carried out (Fig. 18). Unlike the behavior observed in Fig. 8(a), the oscillation indoes not exist for f=0.25 in Fig. 18(a). It is also noticeable that up to θ=44° (approx.) higher values of friction factor result in relatively higheras against that of lower friction factor. Beyond the aforementioned value of θ,starts increasing with the increase in the value of θ. The nature of transmission characteristics (Fig. 18(b)) is very much similar as discussed in Fig. 8(b).

Fig. 15 Effect of dimensionless width of the porous structure L/h1for different fwith υh1=0.8, θ=0°, N=10, γ=0.9 and p=7

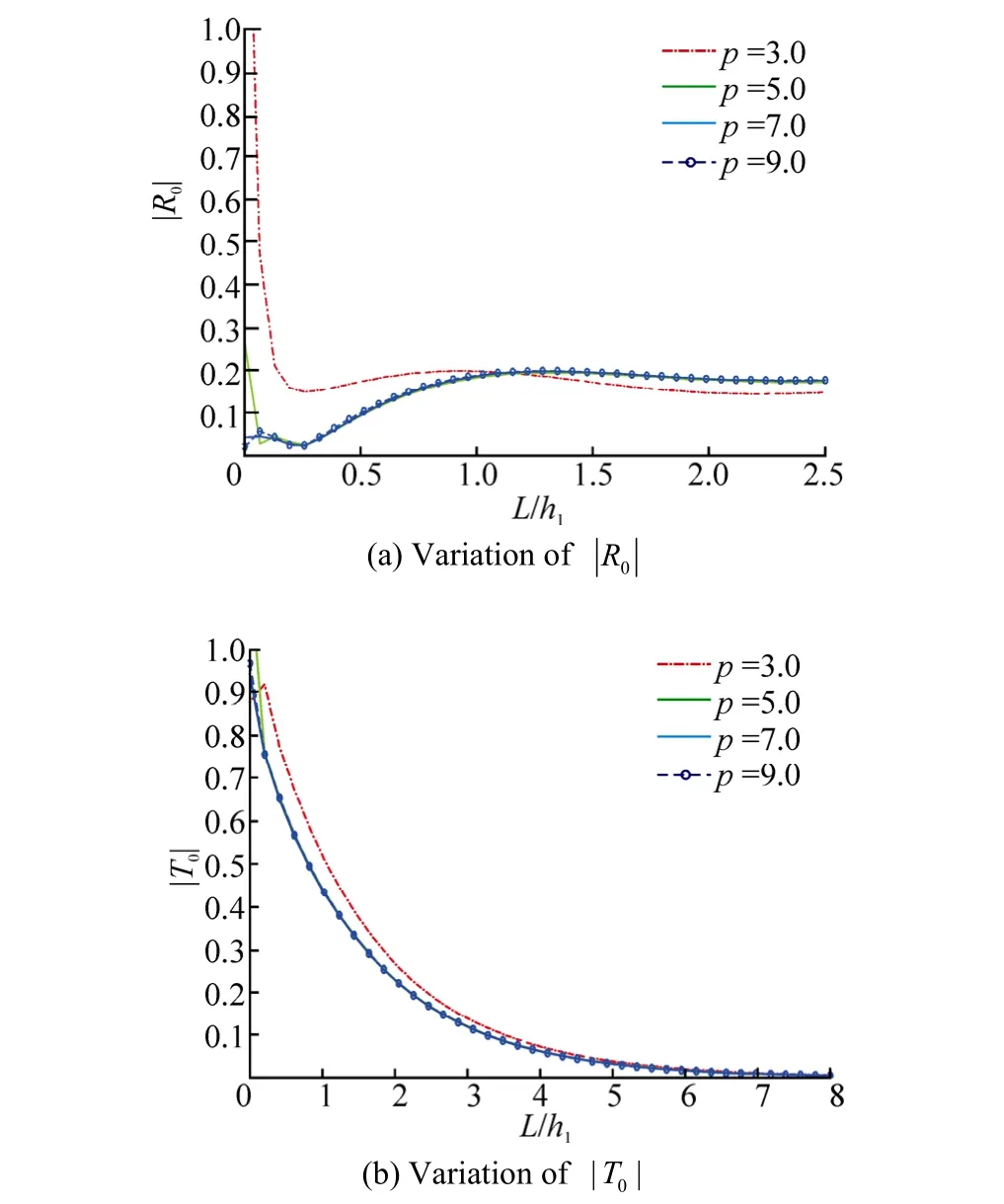
Fig. 16 Effect of dimensionless width of the porous structure L/h1for different pwith υh1=0.8, θ=0°, N=10, γ=0.9 and f=1

Fig. 17 Effect of angle of incidence θ for different γ with υh1=0.8, L/h1=3, N=10, f=1 and p=7

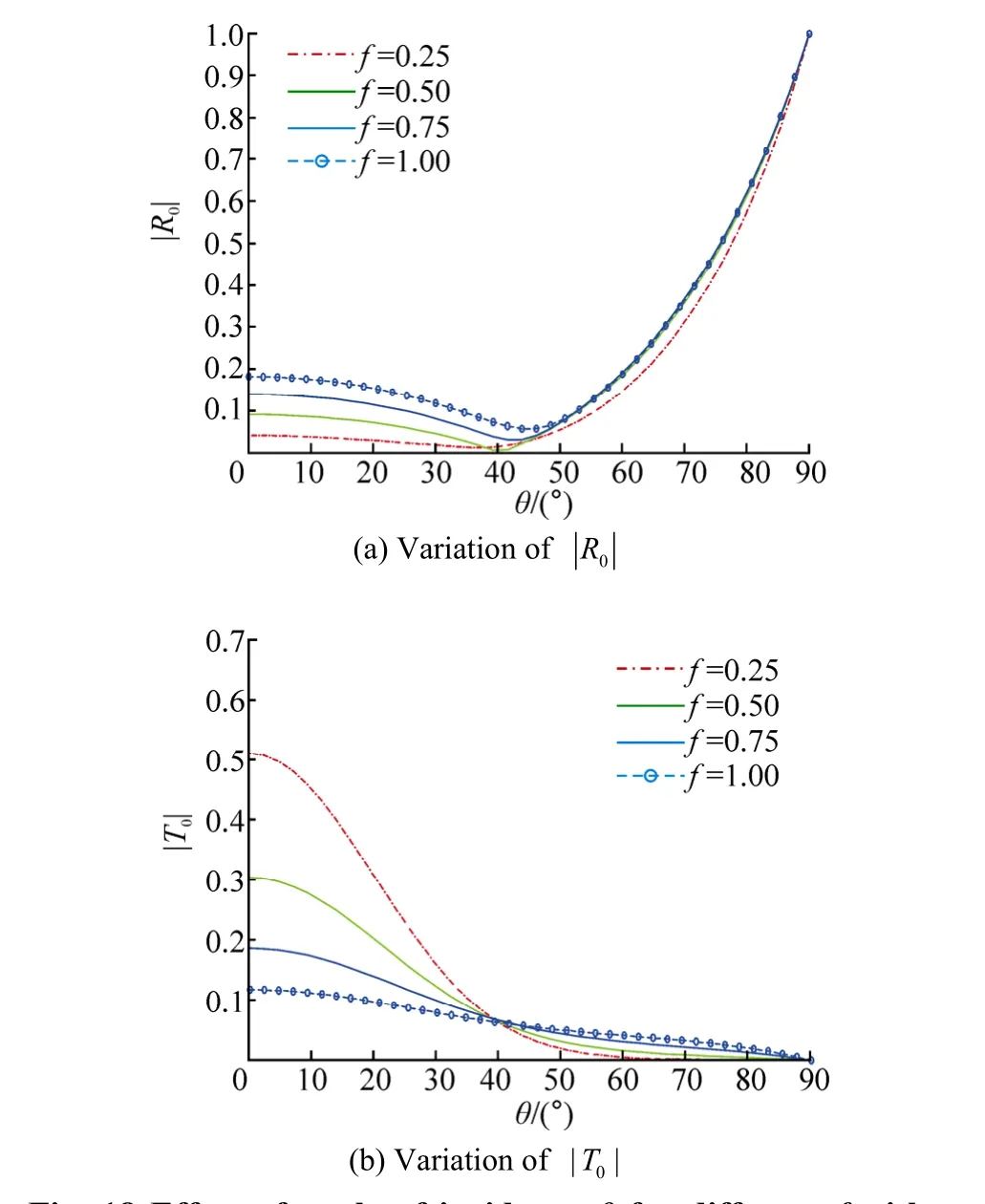
Fig. 18 Effect of angle of incidence θ for different f with υh1=0.8, L/h1=3, N=10, γ=0.9 and p=7

4.2 Energy loss

The energy loss due to the propagation of water wave through the porous structure is discussed in Figs. 19–20.

In Fig. 19, energy loss against L/h1is discussed for different values of porosity and friction factor. Now when L/h1→0 (non-existence of porous structure), Elossshould be zero due to the absence of the porous structure, because incident wave coming from x→−∞ will transmit towards x→∞ without passing through any dissipative medium. It is noticeable that the curves do not exactly start from zero. This is due to the difference in height between region I and region p+2 (Massel, 1993). Each of the energy loss curves increases rapidly with an increase in the value of L/h1and attains a constant value afterwards (Fig. 19(a)). For a thin porous structure, energy loss is independent of the values of porosity taken. Higher porosity gives rise to higher energy loss compared to the lower values of porosity. The analogous pattern exists for the energy loss for different values of friction factor. But the energy loss curves converge to each other at large values of L/h1unlike the curves for different porosity where they do not converge to each other for large values of L/h1.

Fig. 20 illustrates the nature of energy loss against θ for different values of porosity and friction factor. Energy loss for different values of porosity is shown in Fig. 20(a) which is very much similar to that of Fig. 10(a). It is noticeable that oscillation does not exist in the energy loss curve for f=0.25 (Fig. 20(b)) unlike that in Fig. 10(b). Though energy loss for f=0.25 is much less at 0θ= compared to the othervalues of f considered, energy loss increases rapidly and attains a maximum value at other values of f.

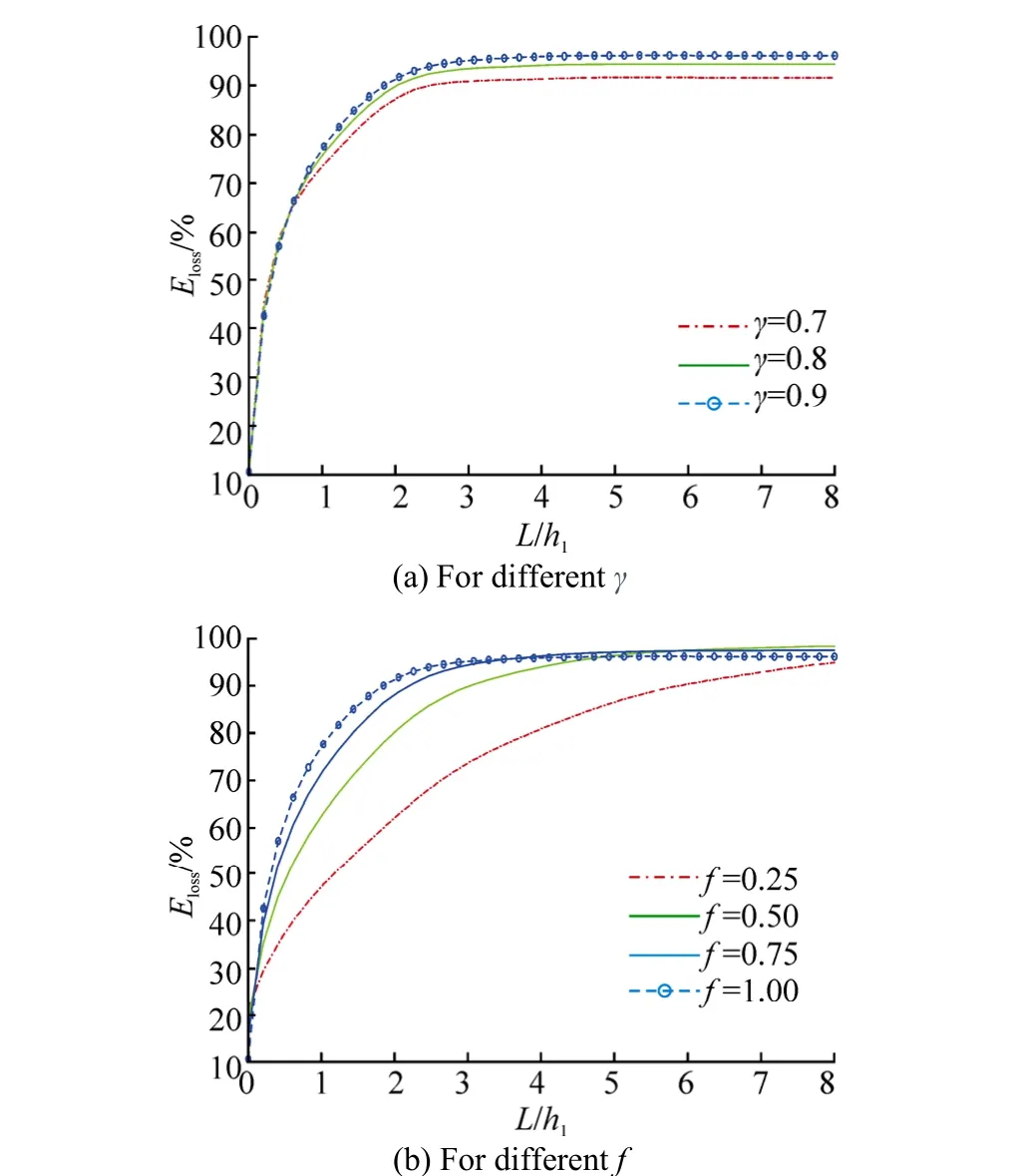
Fig. 19 Energy loss (%)against dimensionless width of the porous structure (L/h1) with υh1=0.8, θ=0°, N=10 and p=7

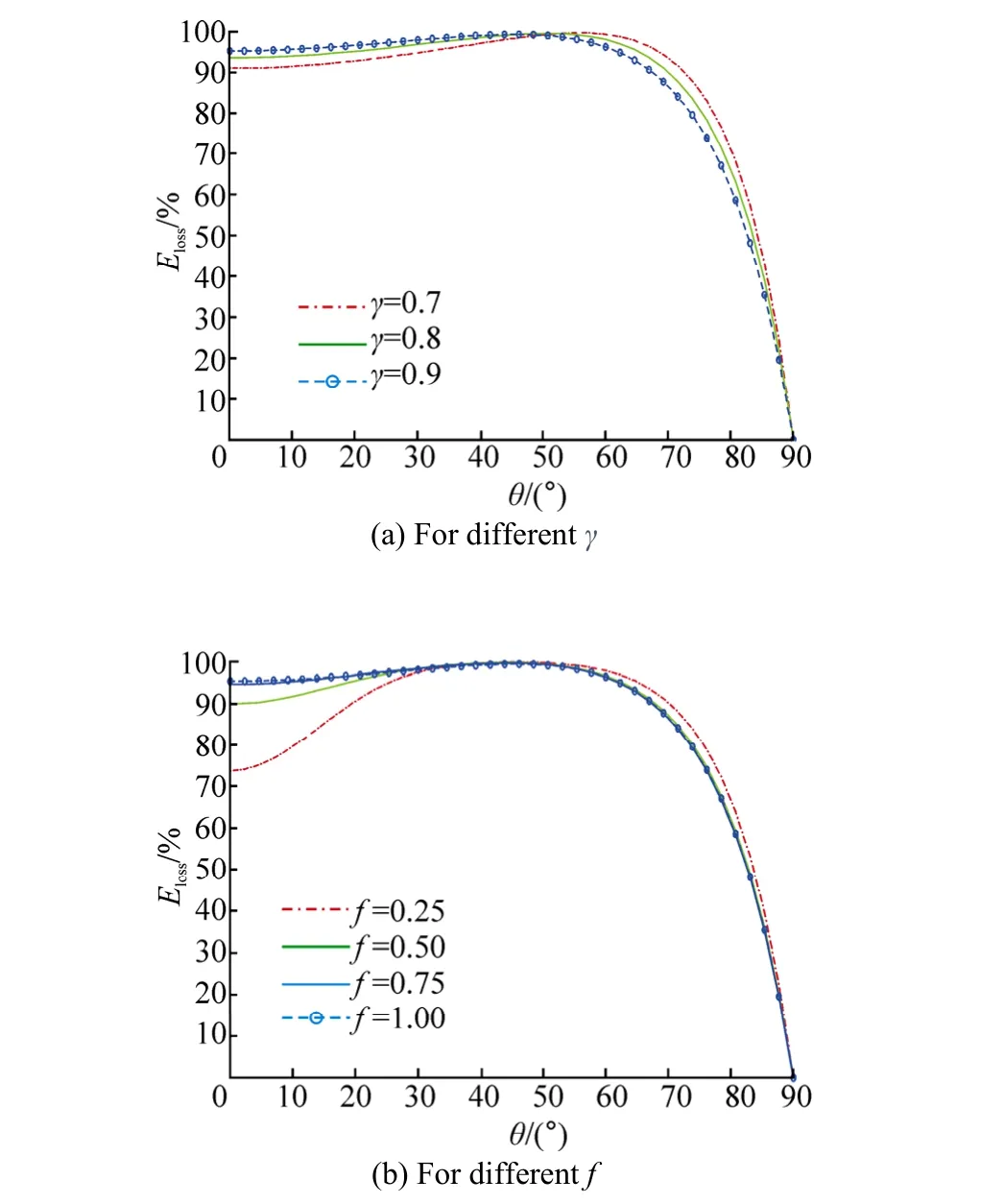
Fig. 20 Energy loss (%) against angle of incidence θ with υh1=0.8, L/h1=3, N=10 and p=7

5 Conclusions

Variations of the reflection coefficient and the dimensionless amplitude of the transmitted progressive wave are studied against the dimensionless width of a porous structure for different values of number of evanescent modes, porosity, friction factor and steps, in the presence of a rigid vertical wall placed at a finite distance from the porous structure. It is observed that for a thin porous structure, irrespective of the parameters considered, the reflection coefficient decreases rapidly from a very high value to attain some constant value which is observed for relatively higher dimensionless width of the porous structure. Reflection is independent of the number of evanescent modes considered whereas higher porosity gives rise to lower reflection. Lower values of friction factor leads to oscillation in reflection coefficient which disappears with an increase in the value of friction factor. Minimum admissible length required for the porous structure in order to be able to act as an effective wave absorber is observed from the very steep portion of the graphs. This admissible length of the porous structure decreases with an increase in number of steps. The dimensionless amplitude of the transmitted progressive wave, irrespective of the different parameters considered, decreases from a very high value attained at lower values of the dimensionless width of the porous structure to zero with an increase in the dimensionless width. The dimensionless amplitude of the transmitted progressive wave is independent of the number of evanescent modes and porosity, but lower friction factor as well as lower number of steps result in higher dimensionless amplitude. The effect of the angle of incident wave on scattering phenomenon for different values of porosity and friction factor is also taken into account. Lower reflection is observed for higher values of porosity up to a fixed range of the angle of incidence beyond which the characteristic reverses and the reflection coefficients start assuming higher values after attaining the minimum reflection. Oscillation in the reflection coefficient for lower value of friction factor is observed. The dimensionless amplitude of the transmitted progressive wave is independent of the values of porosity considered whereas lower friction factor results in higher transmission which reduces with an increase in the angle of incidence. Further the energy loss pattern is studied against dimensionless width of the porous structure and the angle of incidence for different values of porosity and friction factor. The requirement of minimum width of the porous structure is observed. Higher values of porosity and friction factor cause higher energy loss. Up to a fixed range of incident angle, higher porosity results in higher energy loss. Lower value of friction factor shows oscillation in energy loss. A convergence is observed for higher values of the friction factor. For the validity of our mathematical model, we compare our work with Madsen (1974) by plotting reflection coefficient against dimensionless width of the porous structure for different values of porosity and we findexcellent agreement in this regard. This shows that our model will be effective for solving problems of wave scattering by porous structures placed on a p-step bottom.

Acknowledgement

The first author is grateful to the Council of Scientific and Industrial Research (CSIR), Govt. of India for providing him senior research fellowship for pursuing Ph.D. at Indian Institute of Technology Guwahati, India.

Anglin EJ, Cheng L, Freeman WR, Sailora MJ (2008). Porous silicon in drug delivery devices and materials. Advanced Drug Delivery Reviews, 60, 1266-1277.

Blunt MJ (1998). Physically-based network modeling of multiphase flow in intermediate-wet porous media. Journal of Petroleum Science and Engineering, 20(3-4), 117-125.

Cho IH, Koh HJ, Kim JR, Kim MH (2013). Wave scattering by dual submerged horizontal porous plates. Ocean Engineering, 73, 149-158.

Clement TP, Hooker BS, Skeen RS (1996). Macroscopic models for predicting changes in saturated porous media properties caused by microbial growth. Groundwater, 34(5), 934-942.

Dalrymple RA, Losada MA, Martin PA (1991). Reflection and transmission from porous structures under oblique wave attack. Journal of Fluid Mechanics, 224, 625-644.

Das S, Bora SN (2014a). Reflection of oblique ocean water waves by a vertical rectangular porous structure placed on an elevated horizontal bottom. Ocean Engineering, 82, 135-143.

Das S, Bora SN (2014b). Wave damping by a vertical porous structure placed near and away from a rigid vertical wall. Geophysical and Astrological Fluid Dynamics, 108(2), 147-167. Das S, Bora SN (2014c). Reflection of oblique ocean water waves by a vertical porous structure placed on a multi-step impermeable bottom. Applied Ocean Research, 47, 373-385.

Kirby JT, Dalrymple RA (1983). Propagation of obliquely incident water waves over a trench. Journal of Fluid Mechanics, 133, 47-63.

Liu Y, Li YC (2011). Wave interaction with a wave absorbing double curtain-wall breakwater. Ocean Engineering, 38, 1237-1245.

Liu Y, Li YC, Teng B, Dong S (2008). Wave motion over a submerged breakwater with an upper horizontal porous plate and a lower horizontal solid plate. Ocean Engineering, 35(16), 1588-1596.

Losada IJ, Dalrymple RA, Martin OA (1993). Water waves on crown breakwaters. Journal of Waterway, Port and Coastal Engineering, 119(4), 367-380.

Madsen OS (1974). Wave transmission through porous structure. Journal of Waterway, Port and Coastal Engineering, 100, 169-188.

Madsen PA (1983). Wave reflection from a vertical permeable wave absorber. Coastal Engineering, 7(4), 381-396.

Mallayachari V, Sundar V (1994). Reflection characteristics of permeable seawalls. Coastal Engineering, 23(1-2), 135-150.

Massel SR (1993). Extended refraction-diffraction equation for surface waves. Coastal Engineering, 19(1-2), 97-126.

Sollitt CK, Cross RH (1972). Wave transmissions through permeable breakwaters. Proceedings 13th Coastal Engineering Conference, American Society of Civil Engineering, Vancouver, Canada, 1827-1846.

Straub LG, Bowers CE, Herbich JB (1957). Laboratory studies of permeable wave absorber. Proceedings 6thCoastal Engineering Conference, American Society of Civil Engineering, Gainesville, Florida, 729-742.

Sulisz W (1985). Wave reflection and transmission at permeable breakwaters of arbitrary cross section. Coastal Engineering, 9(4), 371-386.

Ward JC (1964). Turbulent flow in porous media. Journal of Hydraulic Division, ASCE, 90(HY5), 1-12.

Xi D, Xu S, Du Y, Yi L (2011). Wave propagation analysis of porous rocks with thermal activated relaxation mechanism. Journal of Applied Geophysics, 73, 289-303.

Zhu S (2001). Water waves within a porous medium on an undulating bed. Coastal Engineering, 42(1), 87-101.

Zhu S, Chwang AT (2001). Analytical study of porous wave absorber. Journal of Engineering Mechanics, 127(4), 326-332.

Author biographies

E-mail: d.santu@iitg.ernet.in

Swaroop Nandan Bora received his M.Sc. in Applied Mathematics from University of Delhi, India and PhD from Dalhousie University, Halifax, Canada. He is presently a Professor in the Department of Mathematics, Indian Institute of Technology Guwahati, India. His research interests focus on water waves, sloshing, river flow, flow through porous media, special functions, etc. He has about 35 research publications to his credit in addition to 10 conference proceedings. He has guided seven PhD students, eighteen M.Sc. studentsand is involved in a number of sponsored projects.

E-mail: swaroop@iitg.ernet.in

Appendix A

Principle of conservation of mass inside a fluid region leads to the following equation known as the equation of continuity:

Now for the steady state flow of fluid having constantdensity, Eq. (A1) reduces to

For a potential flow, i.e., where φ=▽U , the equation of continuity reduces to Laplace’s equation

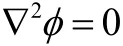
The incompressible equations of motion inside the porous structure can be written in the following form:

The resistance forces in Eq. (A3b) are evaluated by combining known steady and unsteady stress relationships. Under steady state flow conditions the pressure drop through the porous medium is specified by Ward (1964) as

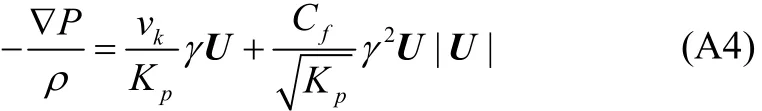
wherevkis the kinematic viscosity,is the intrinsic permeability andis a dimensionless turbulent resistance coefficient of the medium.

It is hypothesized by Sollitt and Cross (1972) that unsteadiness may be accounted for by introducing an additional term which evaluates the added resistance caused by the virtual mass of discrete grains within the medium. The resistance force due to the virtual mass is equal to the product of the displaced fluid mass, the virtual mass coefficient and the acceleration in the approach velocity. The resulting force is distributed over the fluid mass within the pore so that the force per unit mass of fluid is simply

Combining Eqs. (A4) and (A5); and replacing the resistance force in Eq. (A3b) with them, we get

Now, linearization of Eq. (A6) is necessary in order to find an analytical solution and hence, the dissipative stress term is replaced by a linear stress term in U by the following form:

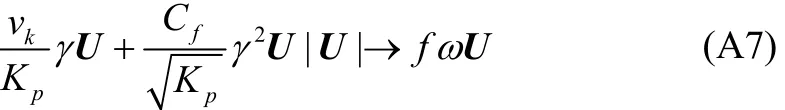
Combination of Eqs. (A6) and (A7) leads to Eq. (1b).

In order to evaluate f, Lorentz’s principle of equivalent work is applied which says that the average rate of energy dissipation should be identical whether evaluated using the true non-linear resistance law or its linearized equivalent. Since the resistance terms of the above relation represent friction force per unit mass acting at a point in the flow field, the following equality (energy dissipation) holds:

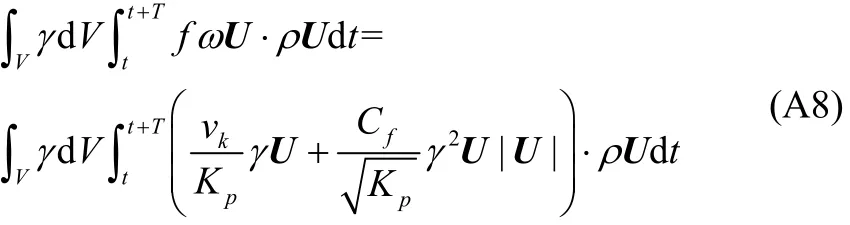
where V is the volume of the flow field and Tis the wave period. Now assuming f to be constant throughout the flow field, the following form can be written

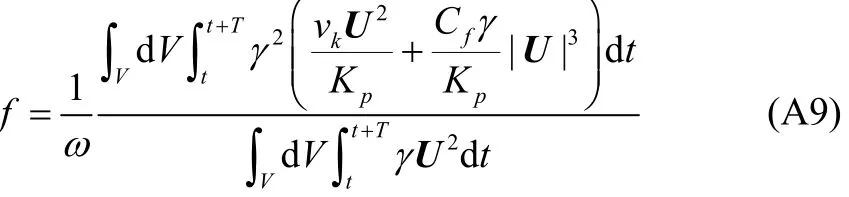
Appendix B

Let us consider U1and U2, respectively, to be the velocities of a fluid at any point inside the water and porous region attached to each other. Then the following relation holds true:

Now, inside the porous region

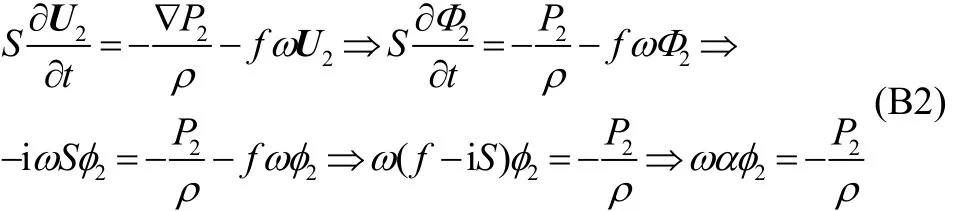
where P1and P2are the dynamic pressures of the water and porous regions, respectively.

In the water region, Bernoulli’s equation gives

Now, along the vertical boundary between the water and porous regions, continuity of pressureresults in (from Eqs. (B2) and (B3)) the following matching condition:

Mass flux per unit volume and unit time inside the porous region is ργU and the same inside the water region is ρU. Along the vertical boundary, the continuity of mass flux implies

Moreover, if both the regions consist of the same medium, then Eqs. (B4) and (B5) reduce to

It is obvious that these matching conditions are valid along the vertical boundary separating any two regions next to each other.

1671-9433(2014)04-0362-151

received his M.Sc. in Mathematics and Computing from Indian Institute of Technology Guwahati, India. Currently, he is pursuing his PhD from Indian Institute of Technology Guwahati, India and has already submitted his doctoral thesis. His research interest includes water waves scattering and flow through porous media. He has to his credit 4 research publications in reputed international journals.

J. Marine Sci. Appl. (2014) 13: 362-376

10.1007/s11804-014-1281-7

Received date: 2014-04-03.

Accepted date: 2014-07-31.

＊Corresponding author Email: swaroop@iitg.ernet.in

© Harbin Engineering University and Springer-Verlag Berlin Heidelberg 2014