Wave Scattering by Porous Bottom Undulation in a Two Layered Channel

Sandip Pauland Soumen De

1. Department of Mathematics, Adamas Institute of Technology, Kolkata 700126, India

2. Department of Applied Mathematics, University of Calcutta, Kolkata 700009, India

Wave Scattering by Porous Bottom Undulation in a Two Layered Channel

Sandip Paul1and Soumen De2＊

1. Department of Mathematics, Adamas Institute of Technology, Kolkata 700126, India

2. Department of Applied Mathematics, University of Calcutta, Kolkata 700009, India

The scattering of plane surface waves by bottom undulations in channel flow consisting of two layers is investigated by assuming that the bed of the channel is composed of porous material. The upper surface of the fluid is bounded by a rigid lid and the channel is unbounded in the horizontal directions. There exists only one wave mode corresponding to an internal wave. For small undulations, a simplified perturbation analysis is used to obtain first order reflection and transmission coefficients in terms of integrals involving the shape function describing the bottom. For sinusoidal bottom undulations and exponentially decaying bottom topography, the first order coefficients are computed. In the case of sinusoidal bottom the first order transmission coefficient is found to vanish identically. The numerical results are depicted graphically in a number of figures.

bottom undulations; two-layer fluid; porous bed; reflection and transmission coefficients; wave scattering

1 Introduction

Wave scattering and generation problems in continuously stratified or multi-layered fluid have recently attracted a good deal of attention. Although, propagation of waves in a two-layer fluid was described by Stokes (1847) long back, till now the literature of two-layer fluid problems is rather limited. Linear wave motion in a two-layer fluid is described in the text books of Lamb (1932) and Landau and Lifshitz (1989). For normally incident waves, the corresponding problem of wave scattering by small bottom undulations in a two-layer fluid with the upper layer extending infinitely upwards and the lower layer having bottom undulations, was studied by Mandal and Basu (1993). The oblique interface wave scattering in such a two-layer fluid was also considered by Mandal and Basu (1994). A number of wave problems in such a two-layer fluid were studied by Dolai and Mandal (1994, 1995), Mandal and Chakrabarti (1995). A two-layer model of an ocean consisting of a layer of fresh water over a deep layer of saline water requires special attention as in this case there exist waves of two different wave numbers, one with lower wave number propagating along the free surface and the other with higher wave number propagating along the interface. Linton and McIver (1995) considered scattering of water waves by a horizontal cylinder in an infinitely deep two-layer fluid where in the upper layer has a free surface. Using linear theory, they examined the interaction of surface and interface waves with a horizontal circular cylinder. The motivation for their work came from a plan to build an underwater pipe-bridge across one of the Norweigian fjords, bodies of water which typically consist of a layer of fresh water on top of salt water. Cadby and Linton (2000) considered three-dimensional water wave scattering in such a two-layer fluid. They developed a general three-dimensional linear scattering theory and then illustrated it by solving problems involving submerged spheres.

Much work has been done on wave/structure interactions in such fluid region approximating the free surface by a rigid lid. With the free surface approximated by rigid lid Sturova (1994), for example, has studied the radiation of wave by an oscillating cylinder which is also moving uniformly in a direction perpendicular to its axis. Sturova (1999) considered the radiation and scattering problem in a cylinder in both a two and a three layer fluid bounded above and below by rigid horizontal walls. Gavrilov et al. (1999) also investigated the effects of a smooth pycnocline on wave scattering, again for horizontal circular cylinder where the fluid is bounded above and below by rigid walls.

Sherief et al. (2003) investigated the motion generated by a vertical wave-maker immersed in a two-layer fluid, the prescribed normal velocity on the wave-maker varying with depth and harmonically with time. The wave-maker was also assumed tobe porous. Sherief et al. (2004) also investigated a vertical cylindrical porouswave-maker immersed in a two layer fluid. Chamberlain and Porter (2005) considered two-layer fluid problem involving bottom variation while Ten and Kashiwagi (2004), Kashiwagi et al. (2006) studied hydrodynamics of a body floating in a two-layer fluid. Mase and Takeba (1994), Zhu (2001) and Silva et al. (2002) investigates the wave scattering problem involving porous bed. Martha et al. (2007) considered the problem of oblique water-wave scattering by small undulation on porous sea bed. They obtain the first order reflection and transmission coefficients. The problem ofoblique wave propagation over a small deformation in a channel flow consisting of two layers was considered by Mahapatra and Bora (2012).

In the present paper scattering by porous bottom undulation in a two layered channel is investigated. Using linear theory, the problem is formulated as a coupled boundary value problem for the two potential functions describing the fluid motion in each of two layers. A simplified perturbation technique is employed to reduce the original boundary value problem coupled one upto first order. This problem is solved here by a method, based on the Fourier transform technique, to obtain the first order reflection and transmission coefficients in terms of integrals involving the shape function describing the bottom undulations. The first-order coefficients are depicted graphically against the wave number for two different shape functions. The effect of porosity is observed in the numerical results.

2 Mathematical formulations

We consider a two-layer invicide, incompressible fluid flowing through a channel with upper layer bounded by a rigid lid, while the lower layer has small cylindrical undulations at the porous bottom. Here a two dimensional co-ordinate system is chosen in such a way that 'y h=-denotes the position of the rigid plate and 0y= denotes the undisturbed interface while y-axis directed vertically downwards. The bottom of the lower layer can be represented by, where ε is a dimensionless small quantity, measures the smallness of the deformation and ()cx is a bounded and continuously differentiable function describing the shape of the undulating bottom, such thatThus the lower layer is of uniform finite depth h below the mean interface far away from the undulations on either side. As the fluid motion is irrotational, the time dependent harmonic velocity potentials of the upper and lower layer can be described byand, where σ is the angular frequency of the incoming wave. The density of the upper fluid isand the lower fluid is. The functions (,)xyψ and (,)xyφ satisfy

The linearized boundary conditions at the interface and the two boundaries of the channel are given by

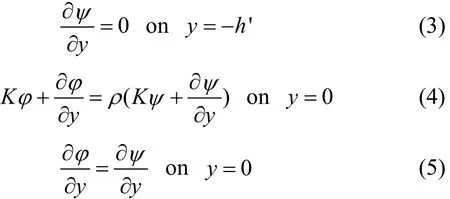
and

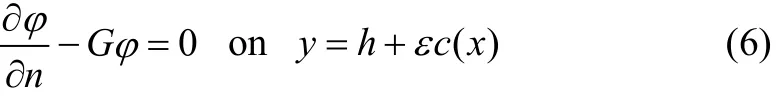
The velocity potentials of the progressive interface wave train coming from the negative infinity areandin the lower and upper fluids, ? whereandhas the following forms:

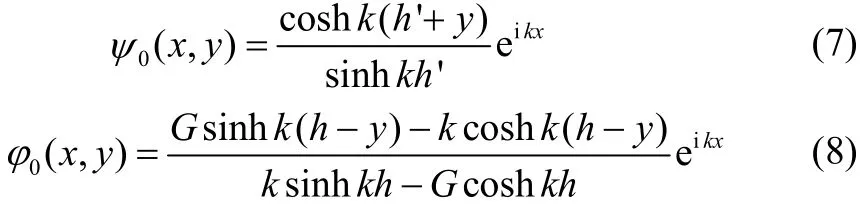
where k is real, positive and satisfies the dispersion relation

where

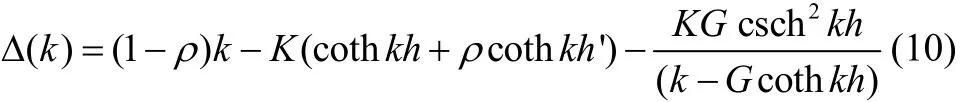
The dispersion equation has exactly one positive real root, m ( 0)m＞ , say; describing mode of the wave propagating through the interface. Since upper layer is bounded by a rigid lid, there is only one wave mode, corresponding to an internal wave. The explanation of roots of the dispersion equation has been given in the Appendix.

The progressive waves of mode m in the upper and lower fluid are given by the velocity potentials

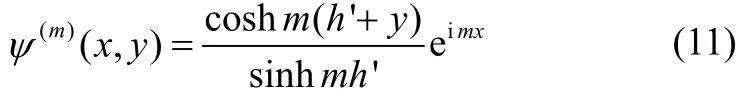
and

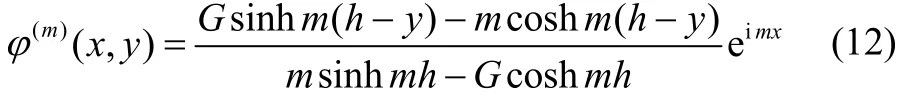
When a train of progressive wave with mode m incident upon the undulating porous sea bottom, it produces reflected wave train in the negative x direction for x→-∞and transmitted wave train in the positive x direction for x→+∞ mode m. These conditions can be mathematically expressed as far field conditions for ψ and φ by

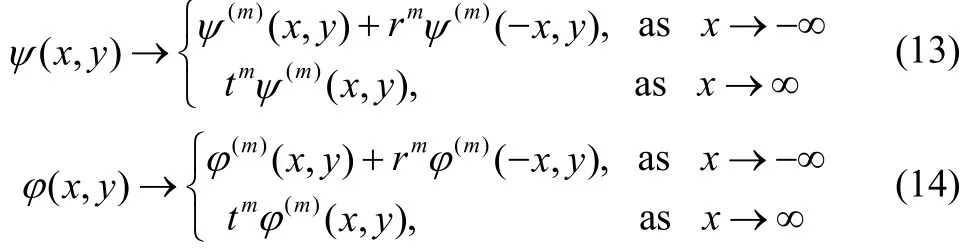
where rmand tmdenotes the reflection and transmission coefficients corresponding to the reflected wave andtransmitted wave of mode m respectively.

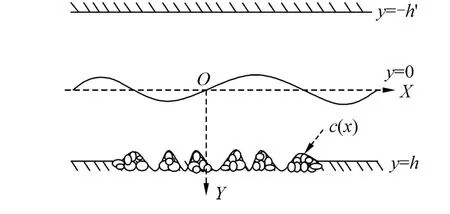
Fig. 1 Sketch of the problem

3 Method of solution

The bottom condition (6) can be expressed approximately as

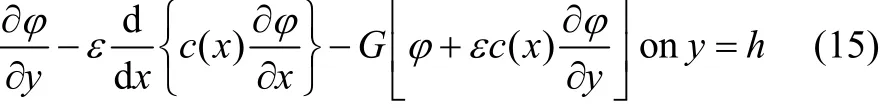
The form of the approximate bottom condition (15) suggests thathave the following perturbational expansions, in terms of the small parameter ε as

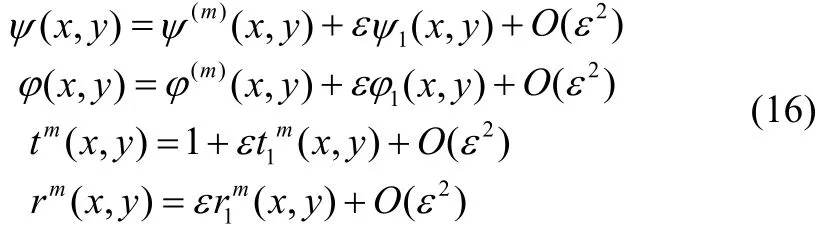
On substituting (16) in Eqs. (3)–(5), (15) and on equating the coefficients of ε from both sides, results the following coupled BVP for first order potential functions as:

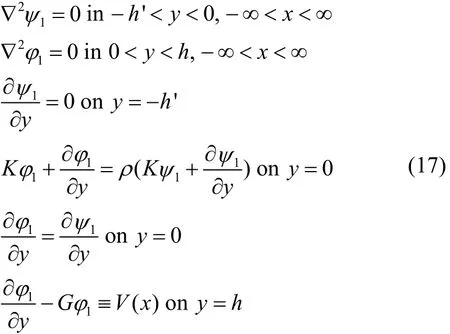
where,

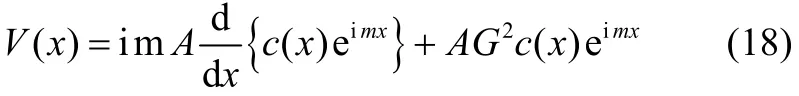
and

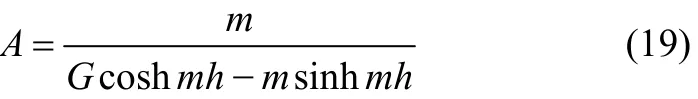
The infinite requirements (13) and (14) give

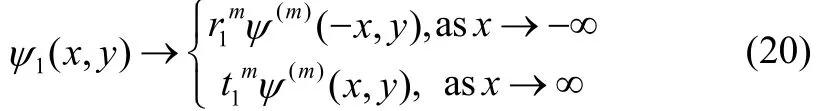
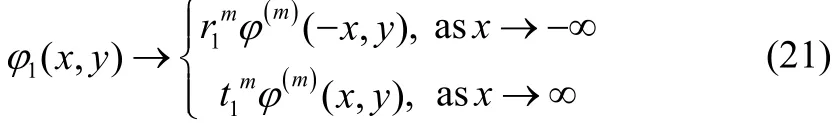
4 First order reflection and transmission coefficients

Solutions of the problem described by Eq. (17) for the potentials ψ1(x,y ) and φ1(x,y) are obtained by using Fourier transform technique.

Let us define the Fourier transform ofandby

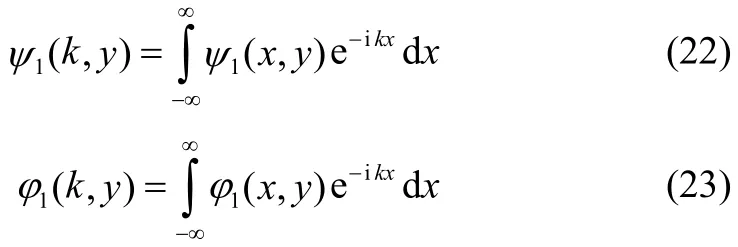
The above transformation exists whenanddecreases exponentially as |x|→∞ and it is possible if we assume that, k has a small positive imaginary part, i.e, we are replacing k by1ik k+ .

To decouple the BVP (17) we write

so that

where ()px is an unknown function.

We get the following boundary value problems

and

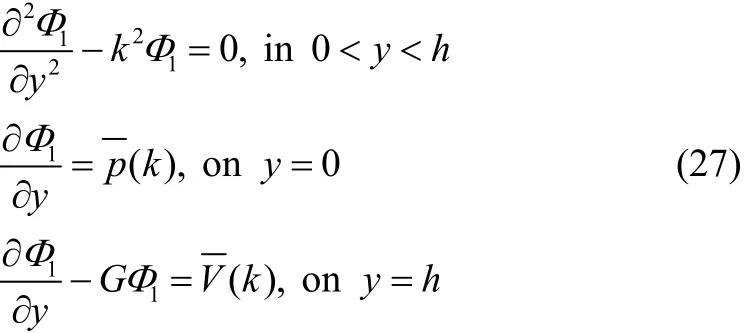
where,p(k) and V(k) respectively, given by

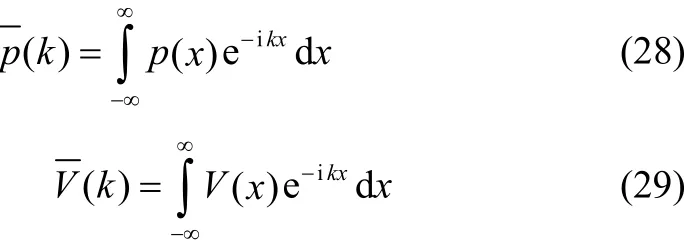
The solution of the BVP (26)–(27) can be expressed as

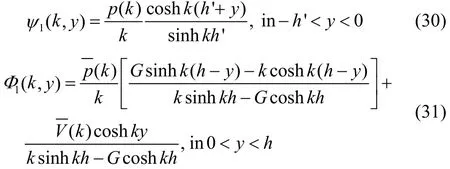
where p(k)is given by

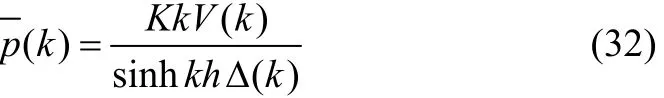
Using (30) and (31), we get

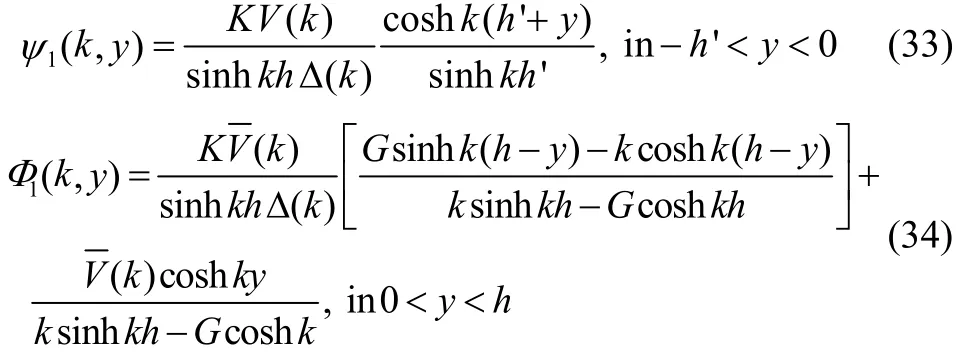
By inverse Fourier transform, Eqs. (33) and (34) gives

Therefore,

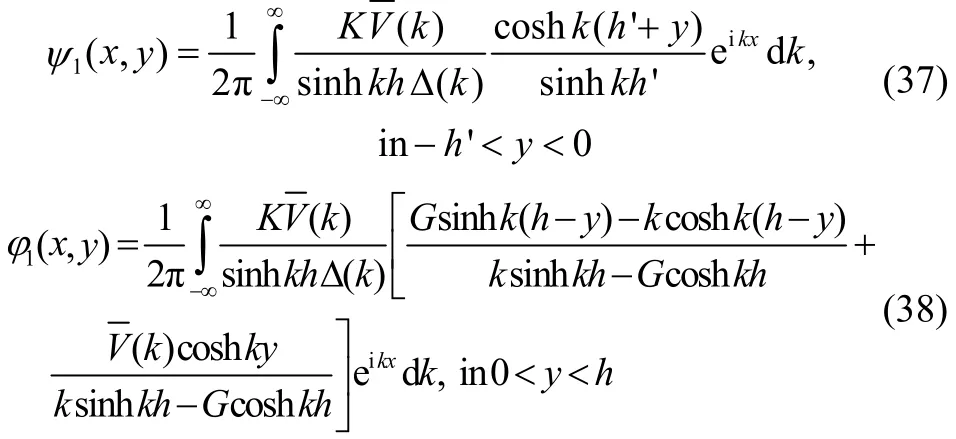
Now, since Δ(k)=Δ(-k ), we can write

The integrands on the right hand side of (39) and (40) has singularities at the zeros ofAsthe dispersion equation has only two real values of k and an infinite no of valuessatisfying the equation

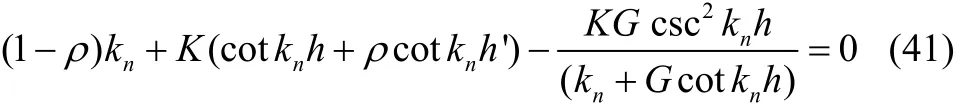
The first order reflection and transmission coefficientsandare obtained by making x→ ∓ ∞ in (39) and (40) and comparing with the infinite requirements (20) and (21) respectively.

As x→∞ the transmission coefficient is obtained by rotating the contour of integration involving eikxinto a contour in the first quadrant by an angleso that the pole at k m= lies inside it and the contour of the integration involvinginto the fourth quadrant by the same angle θ. Then the integrand involvinghas no effect in calculating1(,)xyψ and1(,)xyφ . By complex integration technique we get

where,

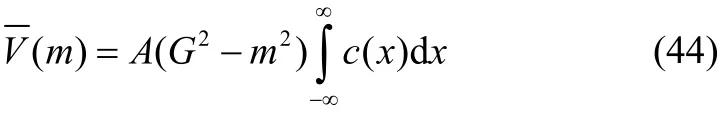
Similarly, as ||x→-∞ the first order reflection coefficient is obtained from the analysis of the behavior ofandin Eqs. (39) and (40) by rotating the path of the second integrals into a contour in the first quadrant, so that we must include the residue term at k m= . In this case the term involving eikxhas no contribution in the expressions ofandand these are:

where,

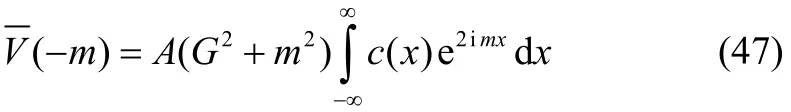
Comparing (42) and (43), (45) and (46) with (20) and (21), we get the first order coefficients as:

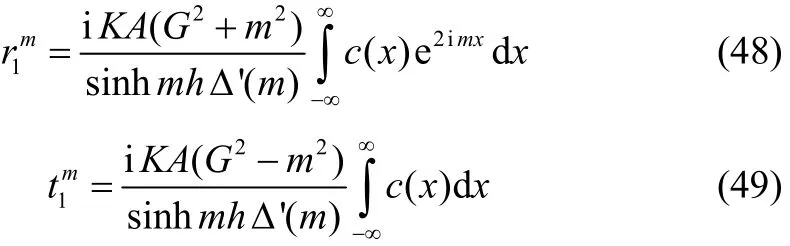
where ()mΔ and A are given by equations (10) and (19) respectively.

5 Numerical results

Example1: For sinusoidal undulations at the bottom of the two-layer fluid, the shape function ()cx as

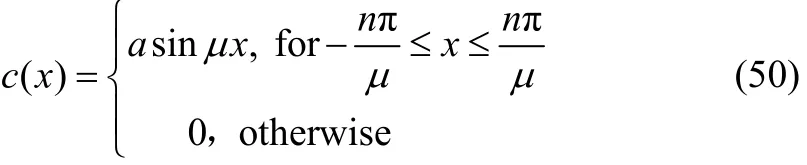
where n is a positive integer. a and μ are the amplitude of the sinusoidal ripple on the bottom surface and the ripple wave number respectively.

Substitute (50) in the expressions (48)–(49), the first order reflection coefficients and the transmission coefficients are given as follows:

where ()mΔ and A are given as in expressions (10) and (19) respectively.

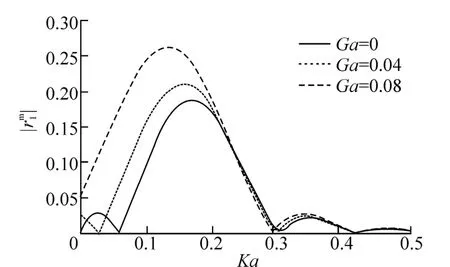
Fig. 2 Sinusoidal undulationsis plotted against Ka for different Ga

The Fig. 2 depicted here is the first order reflection coefficient against Ka. The graph plotted for ρ=0.05,and three different values of Ga, viz. 0.0, 0.04, 0.08. The results obtained here agree with the known results when the bed has no porous effect (Ga=0.0). We have considered a very small density ratio for sake of batter interfacial effect, but it can take any value less than one. In the expression (51),is unbounded when μ～2m, i.e.. The graph showing that, the energy reflection increases with the porous effect. Fig. 3 showing the reflection coefficients for different values of the bottom ripple number (n=1, 3, 5) and forwhen Ga=0.05 and it is clearly seen that the peak values of the coefficients increases. Which shows that, if the ripple number increases indefinitely, the first order coefficients become unbounded for certain value of Ka .

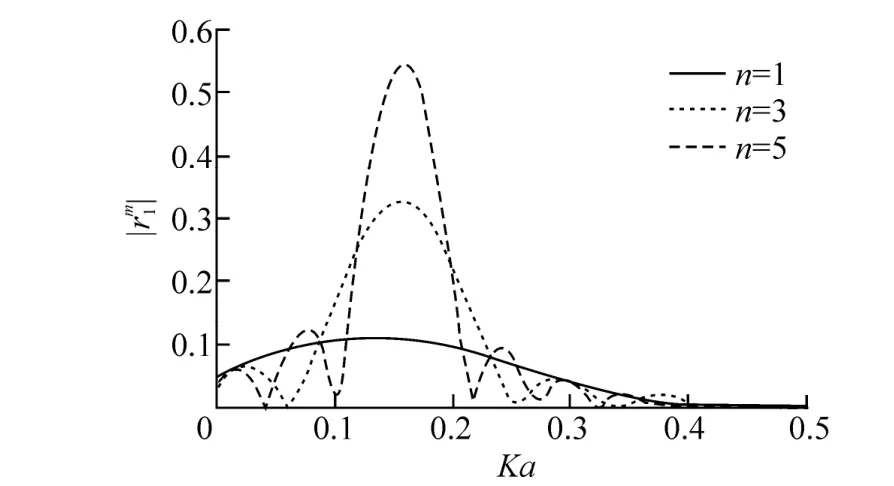
Fig. 3 Sinusoidal undulationsis plotted against Ka for different n

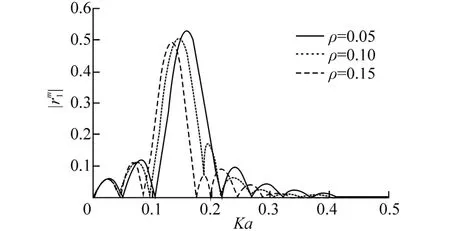
Fig. 4 Sinusoidal undulationsis plotted against Ka for different ρ

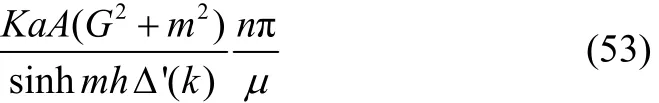
Example 2: We consider the shape function c(x) in the form of an exponentially decaying bottom as

where a and μ are the amplitude of the ripple on the bottom surface and the ripple wave number respectively. On substitution (54) in the expressions (48)–(49), the first order reflection and transmission coefficients are given as follows:

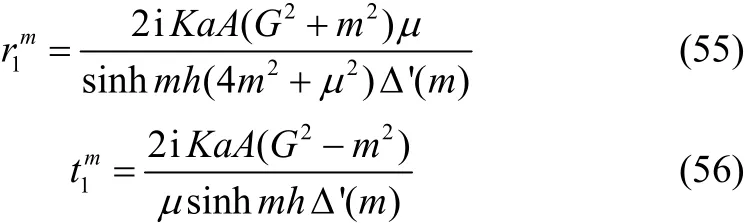
where ()mΔ and A are given by the expressions (10) and (19).

The graphs depicts in Figs. 5 and 6 areandas a function of Ka for three different values of Ga (viz. 0.0, 0.04, 0.08) andIneach of these figures the peak value increases as with porous effect parameter.

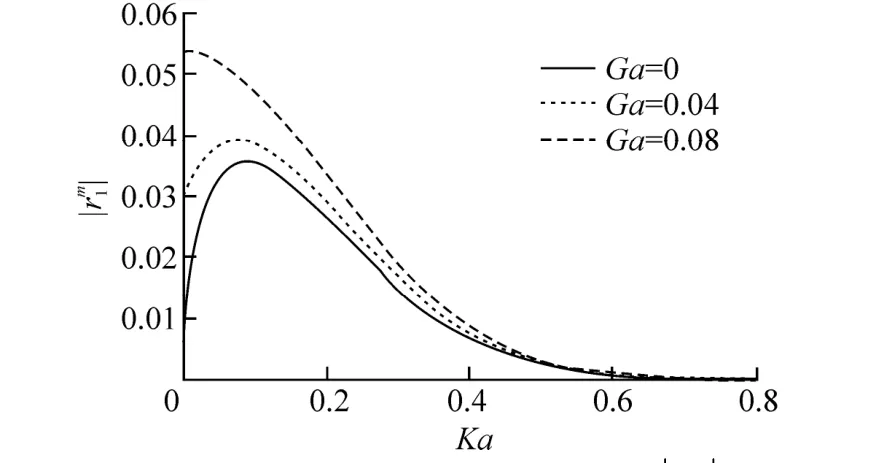
Fig. 5 Exponentially decaying bottomis plotted against Ka for different Ga

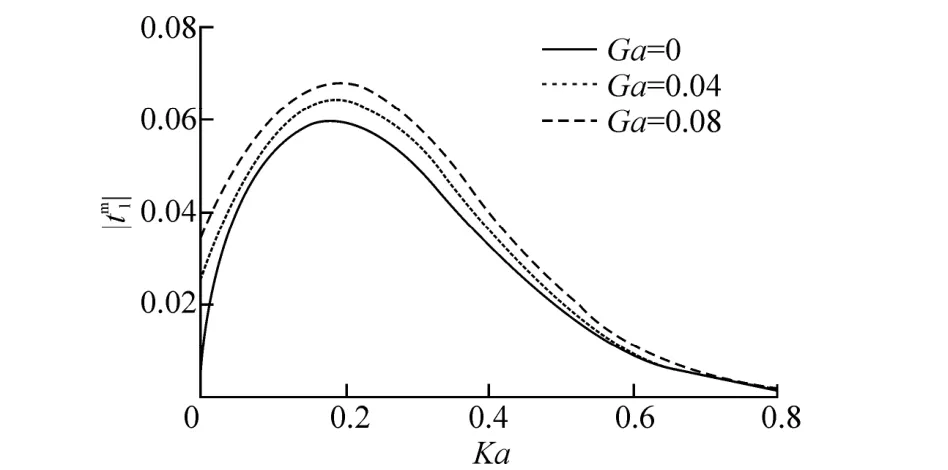
Fig. 6 Exponentially decaying bottomis plotted against Ka for different Ga

Fig. 7 Exponentially decaying bottomis plotted against Ka for different ρ

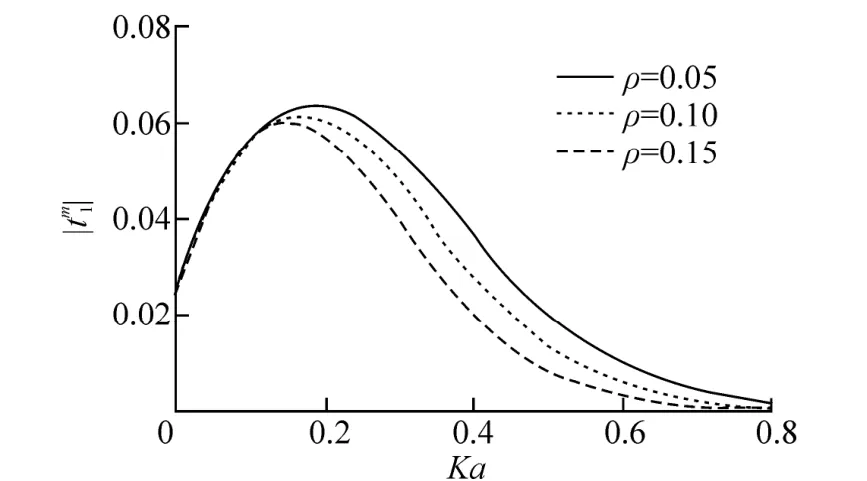
Fig. 8 Exponentially decaying bottomis plotted against Ka for different ρ

In Figs. 7 and 8, reflection and transmission coefficientsandare depicted against Ka for different values of the density ratio ρ for Ga=0.04, h=5a, '5,h a= aμ =0.47. In each of these two figures it is observed that as ρ increases the peak value ofanddecreases. Thus the first order coefficients are quite sensitive to the density ratio.

6 Conclusions

Scattering of surface waves by porous bottom undulation in a two layered channel is investigated. Using a simplified perturbation analysis, the problem is reduced upto first order to a coupled boundary value problem. The boundary value problem is solved by Fourier transform technique. First order reflection and transmission coefficients are obtained in terms of integrals involving the shape function representing the bottom undulations. The bottom undulations are described by sinusoidal ripples on an otherwise flat bed and also by an exponentially decaying profile. For the important case of sinusoidal bottom undulations, the first-order correction for the reflection coefficient is depicted graphically against the wave number, while the same for transmission coefficient vanishes identically. For the case of exponentially decaying bottom topography the first order corrections to reflection and transmission coefficients are also depicted graphically. It is observed that the reflection coefficient increases with increasing porous effect. Also for the sinusoidal bottom the wave reflection increases as the ripple number increases.

Cadby JR, Linton CM (2000). Three dimensional water-waves scattering in two-layer fluid. Journal of Fluid Mechanics, 423, 155-173.

Chamberlain PG, Porter D (2005). Wave scattering in a two-layer fluid of varying depth. Journal of Fluid Mechanics, 524, 207-228. Das D, Mandal BN (2005). A note on solution of the dispersion equation for small-amplitude internal waves. Archives of Mechanics, 57(6), 493-501.

Dolai DP, Mandal BN (1994). Interface waves due to a vertical cylindrical wavemaker in the presence of interfacial tension. Revue Roumaine des Sciences Techniques-Series de Mecanique Appliquee, 39, 659-665.

Dolai DP, Mandal BN (1995), Oblique interface waves against a nearly vertical cliff in two superposed fluids. Proceedings of the Indian National Science Academy, 61(1), 53-72.

Gavrilov N, Ermanyuk E, Sturova I (1999). Scattering of internal waves by a circular cylinder submerged in a stratified fluid. Proceedings 22nd Symposium on Naval Hydrodynamics, Washington DC, USA, 907-919.

Kashiwagi M, Ten I, Yasunaga M (2006). Hydrodynamics of a body floating in a two-layer fluid of finite depth. Part 2. Diffraction problem and wave-induced motions. Journal of Marine Science and Technology, 11(3), 150-164.

Lamb H (1932). Hydrodynamics. Cambridge University Press, Cambridge, 18-62.

Landau LD, Lifshitz EM (1989). Fluid mechanics. Pergamon Press, Oxford, UK.

Linton CM, McIver M (1995). The interaction of waves with horizontal cylinders in two-layer fluids. Journal of Fluid Mechanics, 304, 213-229.

Mandal BN, Basu U (1993). Diffraction of interface waves by a bottom deformation. Archives of Mechanics, 45, 271-277.

Mandal BN, Basu U (1994). Oblique interface wave diffraction bya small bottom deformation in the presence of interfacial tension. Revue Roumaine des Sciences Techniques-Series de Mecanique Appliquee, 39, 525-531.

Mandal BN, Chakrabarti RN (1995). Potential due to a horizontal ring sources in a two-fluid medium. Proceedings of the Indian National Science Academy, 61, 433-439.

Martha SC, Bora SN, Chakrabarti A (2007). Oblique water-wave scattering by small undulation on a porous sea-bed. Applied Ocean Research, 29(1-2), 86-90.

Mase H, Takeba K (1994). Bragg scattering of waves over porous rippled bed. Proceedings of the 24th International Conference on Coastal Engineering (ICCE ’94), Kobe, Japan, 635-649.

Mohapatra S, Bora SN (2012). Oblique water wave scattering by bottom undulation in a two-layer fluid flowing through a channel. Journal of Marine Science and Application, 11(3), 276-285.

Sherief HH, Faltas MS, Saad EI (2003). Forced gravity waves in two layered fluids with the upper fluid having a free surface. Canadian Journal of Physics, 81(4), 675-689.

Sherief HH, Faltas MS, Saad EI (2004). Axisymmetric gravity waves in two-layered fluids with the upper fluid having a free surface. Wave Motion, 40(2), 143-161.

Silva R, Salles P, Palacio A (2002). Linear wave propagating over a rapidly varying finite porous bed. Coastal Engineering, 44(3), 239-260.

Stokes GG (1847). On the theory of oscillatory waves. Transactions of Cambridge Philosophical Society, 8, 441-455 (Reprinted in Mathematical and Physical Papers, 1, 314-326.)

Sturova IV (1994). Plane problem of hydrodynamic rocking of a body submerged in a two layer fluid without forward speed. Fluid Dynamics, 29(3), 414-423.

Sturova IV (1999). Problems of radiation and diffraction for a circular cylinder in a stratified fluid. Fluid Dynamics, 34(4), 521-533.

Ten J, Kashiwagi M (2004). Hydrodynamics of a body floating in a two layer fluid of finite depth. Journal of Marine Science and Technnology, 9(3), 127-141.

Zhu S (2001). Water waves within a porous medium on an undulating bed. Coastal Engineering, 42(1), 87-101.

Author biographies

Sandip Paul was born in 1983. He is a assistant professor at Department Mathematics, Adamas Institute Technology, Kolkata, India. His current research interests include water wave problems.

Soumen De was born in 1981. He is a assistant professor at the Department Applied Mathematics, University of Calcutta, India. His current research interests include water wave problems, integral equations, etc.

Appendix: roots of the dispersion equations

Here we find the roots of the dispersion equations in a fluid of finite depth with porous bottom when the upper surface of the fluid is bounded by a rigid lid.

The dispersion equation given by (9) is

The plot (Fig. A1) of the functions Kh(cothkh+ρcothkh')-and (1 )khρ- intersect exactly at one point for Kh＞0 for Kh=0.2,Gh =0.05,ρ=0.05. Similarly when we plot for μ＜or＞1, the result will be the same. Since each of these functions is odd in kh, there are always exactly two real roots occurring as plus and minus of some positive quantity which we denote as m.

When k is purely imaginary, ik κ= for some real κ, the Eq. (A1) becomes

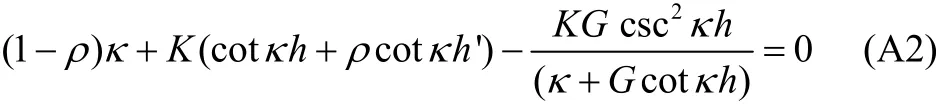
Thus the purely imaginary roots of the Eq. (A2) are obtained from the plots (Fig. A2) of -Kh(cotκh+ρcotκh ')-and (1 )hρκ- against hκ .

It is obvious that there exists an infinite no of purely imaginary roots of the Eq. (A2) given byn=1,2,3…(say).

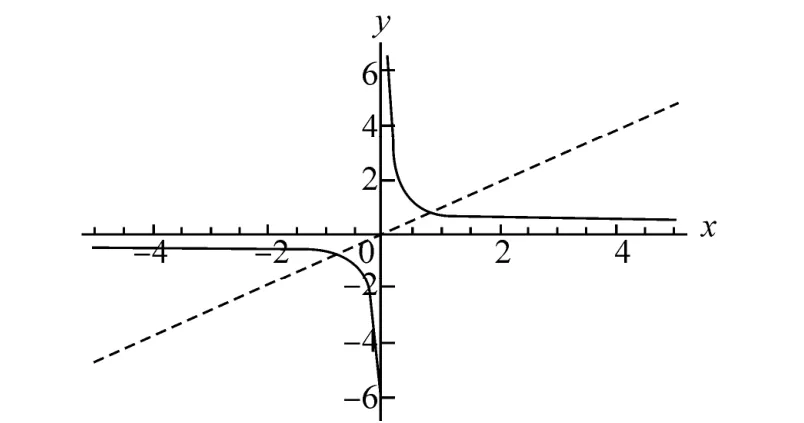
Fig. A1y=Kh(cothkh+ρcothkh′)-

Fig. A2y=-Kh(cotκh+ρcotκh′)-

By Rauche’s theorem of complex variable theory, we can show that the dispersion Eq. (A1) has two real roots, infinite no of purely imaginary roots and there is no other roots (Das and Mandal, 2005).

1671-9433(2014)04-0355-07

J. Marine. Sci. Appl. (2014) 13: 355-361

10.1007/s11804-014-1276-4

date: 2013-11-26.

Accepted date: 2014-07-31.

＊Corresponding author Email: soumenisi@gmail.com

© Harbin Engineering University and Springer-Verlag Berlin Heidelberg 2014