一类热源在边界点的反应扩散系统的边界控制
2014-07-24郭春丽
郭春丽
(四川文理学院数学与财经学院,四川达州635000)
一类热源在边界点的反应扩散系统的边界控制
郭春丽
(四川文理学院数学与财经学院,四川达州635000)
利用边界控制的backstepping方法研究了一类热源在边界点x=1的反应扩散系统.由于热源在边界,backstepping方法中常用的Voltegral变换失效,为了利用backstepping方法设计控制器,文章改进了原有的Voltegral变换,从而设计出反应扩散系统的控制器,最后,通过闭环系统的稳定性验证了控制器的有效性.
反应扩散系统;边界控制;backstepping方法;稳定性
0 前言
热传导的数学模型是众所周知的,常见的热传导现象有化学反应、生物发酵、燃烧问题等,[1]这些常见的现象都涉及到温度的传导问题,而温度的传导问题常用偏微分方程中的反应扩散方程来描述:
ut(x,t)=uxx(x,t)+f(u(x,t))
其中,u(x,t)表示规范化的温度;f是光滑函数,表示热源;f(u(x,t))可以有不同的形式,对于具体的工程问题,有其特定的形式.[1][2]所以,研究反应扩散方程的稳定性问题对实际生活有着重要意义.
对于反应扩散系统,可采用多种控制方式设计控制器实现系统的稳定性,其中边界输出反馈控制方式运用最为广泛.边界输出反馈控制的方法有:Lyapunov函数法、damping法、backstepping方法等.近年来,Miroslav Krstic、Andrey Smyshlyaev 等人将backstepping方法引入到偏微分方程的边界控制中,[3-6]由于该方法计算简单且容易实现,因此得到很大发展.本文就运用边界控制的backstepping方法研究一类反应扩散系统的稳定性问题.
1 问题陈述
考虑如下的反应扩散系统:
(1)
其中,u(x,t)是状态变量,U(t)是控制输入,λ>0是较大的常数.控制系统(1)中反应扩散方程里反应项为λu(1,t),反应项只与右端点x=1处的温度有关系,也就是控制系统(1)所涉及到的是热源在右端的热传导问题.
2 控制的设计
运用backstepping方法设计控制器,引入变换
(2)
其中,k(x,y)和r(x,y)是待定的核函数.[7][8]
变换(2)将控制系统(1)转化为指数稳定的目标系统:[3]
(3)
在(2)式两边关于x求偏导有:
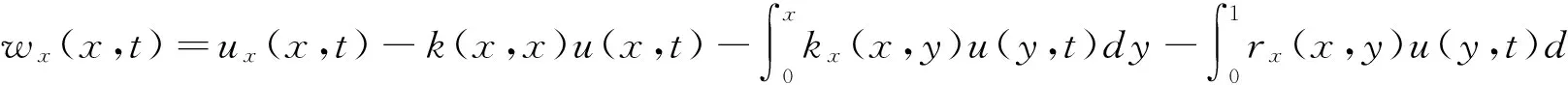
(4)
在上式中取x=1可得控制输入:
U(t)=ux(1,t)=k(1,1)u(1,t)+

(5)
3 核函数的计算
为了得到控制输入(5),需找到核函数k(x,y)和r(x,y),下面由变换(2)将控制系统(1)转化为系统(3)得到核函数满足的方程,然后由核函数满足的方程组求解出核函数.
首先,在变换(2)两边同时关于x求二阶偏导有:
(6)
其中,

类似地,在变换(2)两边同时关于t求偏导,并由控制系统(1)有:

运用分部积分法和控制系统(1)中的边界条件有:
(7)
由(6)、(7)可得:
(8)
为满足目标系统中的方程wt(x,t)=wxx(x,t),选择核函数满足方程组
及相容性条件

(10)
由wx(0,t)=0、ux(0,t)=0及(4)有:

从而,k(0,0)=0,rx(0,y)=0.由k(0,0)=0和k'(x,x)=0可得k(x,x)=0,因此核函数k(x,y)满足方程组
从而,解得[3]
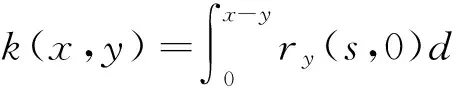
(11)
其次,运用偏微分方程的变量分离法解核函数r(x,y),然后验证相容性的条件(10).设r(x,y)=p(x)q(y),则p(x)和q(y)满足方程组
(12)
其中,a>0是待定的常数.
由(12)解得
p(x)=bcosh(ax),q(y)=csinh(ay-a)
(13)
其中,b,c是待定的常数.
下面通过验证相容性条件,得到常数a,b,c需满足的条件.由(11)、(13)及r(x,y)=p(x)q(y)可得
(14)
由(13)及r(x,y)=p(x)q(y)可得
(15)
从而,由(13)、(14)、(15)及r(x,y)=p(x)q(y)可得
因此,为满足相容性条件(10),取
(16)
则由(13)、(16)及r(x,y)=p(x)q(y)可得,
(17)
由(11)、(17)可得
(18)
4 反馈控制器
由核函数的解(17)、(18)可得到控制系统(1)的反馈控制器为
(19)
事实上,变换(2)是可逆变换,且逆变换具有如下形式
(20)
其中,l(x,y),h(x,y)是待定的核函数.
逆变换(20)将目标系统(3)转化为控制系统(1),运用第3节类似的方法可计算得到逆变换中的核函数,最后由变换(3)、(20)及目标系统的稳定性可证明得到原控制系统(1)在反馈控制器(19)的作用下是指数稳定的[8].
[1] 叶其孝. 反应扩散方程简介[J]. 数学的实践与认识,1984(2):48-57.
[2] J.Smoller.Shockwaveandreaction-diffusionequations[M]. Springer-Verlag, New York: 1994:43.
[3] M. Krstic, A. Smyshlyaev.BoundarycontrolofPDEs:Acourseonbacksteppingdesign[M]. SIAM, Philadelphia,2008:72.
[4] D. M. Boskovi, M. Krstic.Stabilizationofasolidpropellantrocketinstabilitybystatefeedback[J]. International Journal of Robust and Nonlinear Control, 2003(13):483-495.
[5] A. Smyshlyaev, M. Krstic.Closedformboundarystatefeedbacksforaclassofpartialintegro-differentialequations[J]. IEEE Transanction on Automatic Control, 2004(49):2185-2202.
[6] M. Krstic , B. Z .Guo , A.Balogh , A. Smyshlyaev.Output-feedbackstabilizationofanunstablewaveequation[J]. Automatic , 2008(44):63-74.
[7] Z. C. Zhou, C. L. Guo.Stabilizationoflinearheatequationwithaheatsourceatintermediatepointbyboundarycontrol[J].Automatica, 2013(49): 448-456.
[8] C. L. Guo, C. K. Xie, Z. C. Zhou.Stabilizationofaspatiallynon-causalreaction-diffusionequationbyboundarycontrol[J].Int. J. Robust. Nonlinear Control, 2012(10):64.
[责任编辑 邓 杰]
Stabilization of a Reaction-diffusion Equation with the Heat Source on the Boundary
GUO Chun-li
(Mathematics and Finance-Economics Department of Sichuan University of Arts and Science, Dazhou Sichuan 635000, China)
In this paper, the stabilization of a reaction-diffusion equation with the heat source on the boundary is considered by using boundary control. For the new system, the Voltegral transformation of backstarting method is invalid. A new back-stepping transformation is introduced,in which there are two kernels. Because the number of kernels is increased, the kernel equations and computation are more complicated. Through a series of mathematical tricks, the exact solutions of kernels are obtained, and a control law is obtained specifically. Finally, stability of the closed-loop system is established.
reaction-diffusion system; back-stepping method; boundary control;stabilization
2013-11-26
四川文理学院资助项目(2012Z002Q)
郭春丽(1987—),女,四川渠县人. 助教,硕士,主要从事应用数学研究.
O231.5
A
1674-5248(2014)02-0023-04
