度量李代数的扩张

贾培佩，马成，张泰

（1.河北金融学院 基础部，河北 保定 071051；2.河北软件职业技术学院 实验实训中心，河北 保定 071002）

1 基本概念与基本结论

1985年，Filippov提出了n－Lie代数（Filippov代数）的概念［1］.而n＝3的情形首先出现在文献［2］中，Nambu利用三元运算描述了3 个变元的类似于古典力学系统的Nambu 力学系统，得到了广义的三元Hamiltoni恒等式.Takhtajan对Nambu力学系统进行了研究，建立了Nambu力学系统与Filippov代数之间的联系［3］.

因为3－李代数与几何学、力学系统及玄论等的密切关系，3－李代数的研究越来越受到人们的关注.例如，Bagger和Lambert利用度量3－李代数建立了多元M2－Branes的场论模型，并且利用其在物理上的应用构造了3－李代数.关于n－李代数（n≥3）结构的更多研究与应用可参见文献［4－9］.

3－李代数是李代数的推广，是具有3－元运算的非结合代数系统.因为其多元运算，3－李代数的结构与李代数有着很大的差异，特别是3－李代数的实现问题，一直是人们关注的焦点.在文献［8］中，利用李代数及线性函数实现了3－李代数，而本文研究利用度量李代数实现3－李代数的方法.

首先介绍本文用到的几个基本概念与基本结论.

设（V，［，］）是李代数，Bv：V⊗V→F 是非退化的对称双线性型，如果Bv满足ad－不变性，即

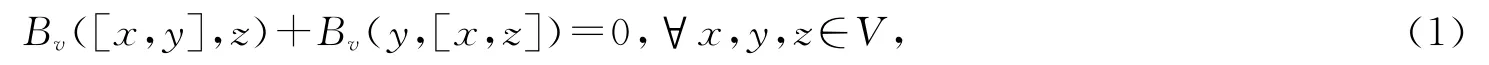
则称（V，［，］，Bv）是度量李代数.

称是域F 上的向量空间L 是3－李代数［1］，如果L 上的斜对称3－元线性运算［，，］：L⊗L⊗L→L，满足下列等式（称为广义的Jacobi等式）

其中σ是对称群S3中的任意元素，τ（σ）等于0或1基于σ是奇置换还是偶置换.

设（L，［，，］）是3－李代数，所有元素［x，y，z］，∀x，y，z∈L 张成的线性空间记为L1＝［L，L，L］，称为L的导代数.

对任意非退化的对称双线性型B：L⊗L→F，如果B 满足ad－不变性，即

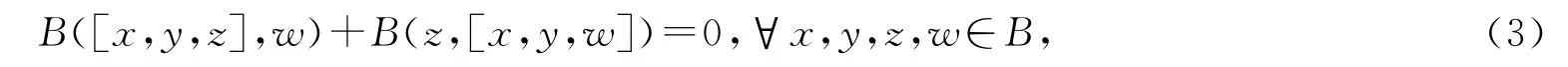
则称（L，［，，］，B）是度量3－李代数，B 称为此3－李代数的度量.

对于L 的子空间W，称W⊥＝｛x∈L｜B（x，y）＝0，∀y∈W｝为W 的正交补空间.由式（3）可知，如果W是L 的理想（即［W，L，L］⊆W），则W⊥也是理想.如果子空间W ⊆W⊥，则称W 是迷向的子空间.子空间Z（L）＝｛x∈L｜［x，L，L］＝0｝称为3－李代数L 的中心.显然，Z（L）是L 的理想.

引理1［8］设（V，［，］）是李代数，V＊是V 的对偶空间.设f∈V＊满足f（［x，y］）＝0，∀x，y∈V，则V 按下列3－元运算［，，］f构成3－李代数：

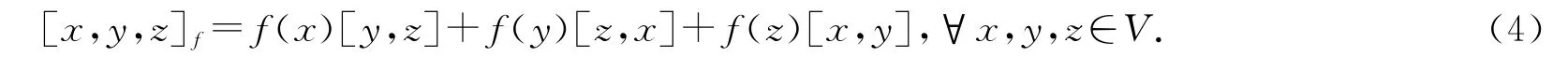
2 度量李代数的扩张

设（V，［，］，Bv）是m－维非Abel的度量李代数，f∈V＊满足f≠0，f（［x，y］）＝0对任意x，y∈V.由引理1可知，V 按运算［，，］f构成3－李代数，但Bv不是3－李代数（V，［，，］f）的度量.

事实上，如果Bv满足

对任意x，y，z，u∈V 成立，那么对∀x，y，z，u∈V，有

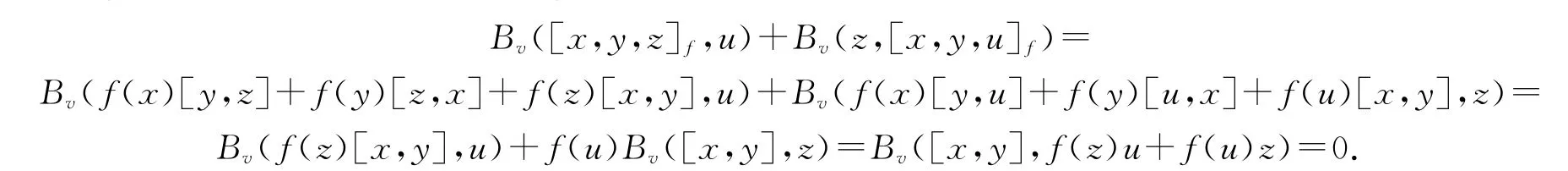
因为f≠0，存在V 的一组基｛x1，…，xm｝使得f（x1）＝1，f（xi）＝0，2≤i≤m，所以对于k≥2，有

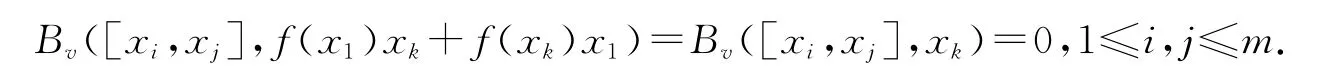
由式（1），B（［xi，xj］，x1）＝B（xi，［xj，x1］）＝0，所以Bv（V1，V）＝0.由Bv的非退化性可知，V1＝0，即（V，［，］，Bv）是Abel的度量李代数，与已知矛盾，因此得到下列结论.

定理1 设（V，［，］，Bv）是非Abel的度量李代数，f∈V＊满足f≠0且f（［x，y］）＝0，∀x，y∈V，则Bv在3－李代数（V，［，，］f）上不满足ad－不变性，其中［，，］f如等式（1）定义，则Bv不是3－李代数（V，［，，］f）上的度量.

定理2 设（V，［，］，Bv）是非Abel的度量李代数，f∈V＊满足f≠0且f（［x，y］）＝0，∀x，y∈V，记L＝V+Fc是V 的1－维扩张，其中c∈／V，则（L，［，，］cf）是3－李代数，其中

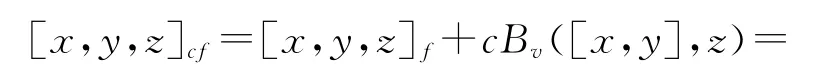
证明 由式（1），［，，］cf是斜对称的3－元线性运算.下面证明［，，］cf满足式（2）.对任意x，y，z，u，v∈V，由式（6）可知，

又因为

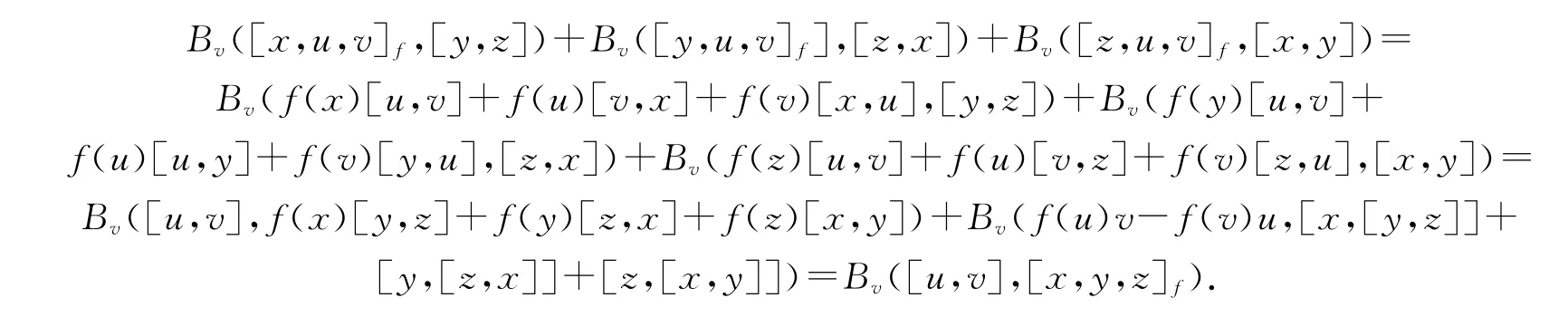
因此，

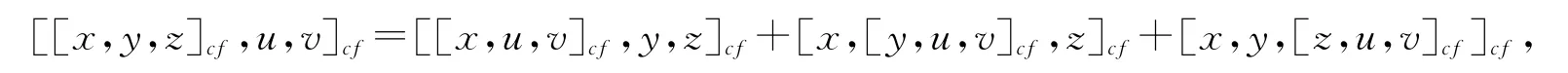
所以（L，［，，］cf）是3－李代数.

例1 设（V，［，］，Bv）是5－维度量李代数，｛x1，x2，x3，x4，x5｝是V 的一组基，其中，

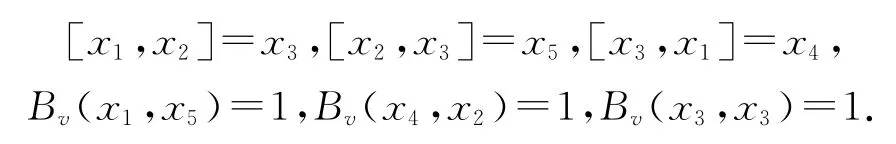
对于f∈V＊满足f（x1）＝1，f（xi）＝0，2≤i≤5.设c∈／V，L＝V+Fc，由定理2，（L，［，，］cf）是3－李代数，在基｛x1，x2，x3，x4，x5｝下的乘法为［x1，x2，x3］cf＝x5＋c.

定理3 设（V，［，］，Bv）是域F 上的m－维度量李代数，f∈V＊满足f≠0，f（V1）＝0.若G＝V+Fc0+fc－1是线性空间的直和，其中c0，c－1∈／V，那么（G，［，，］，B）是（m＋2）－维度量3－李代数，其中对任意的x1，x2，x3∈V，有

B：G⊗G→G 是对称双线性型，满足

其中［，，］f由式（4）定义.

证明 对∀x1，x2，x3，x4，x5∈V，由式（6）可知，［x1，x2，x3］＝［x1，x2，x3］cf.又由定理2可知，

由式（7）可得，对任意x1，x2，x3，x4∈V，有

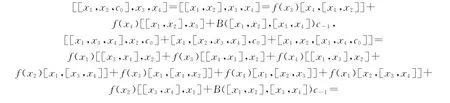
所以，

因此得到（G，［，，］）是3－李代数.

由式（7）和式（8）可知，B：G⊗G→G 是非退化的对称双线性型，且对任意x1，x2，x3∈V，有

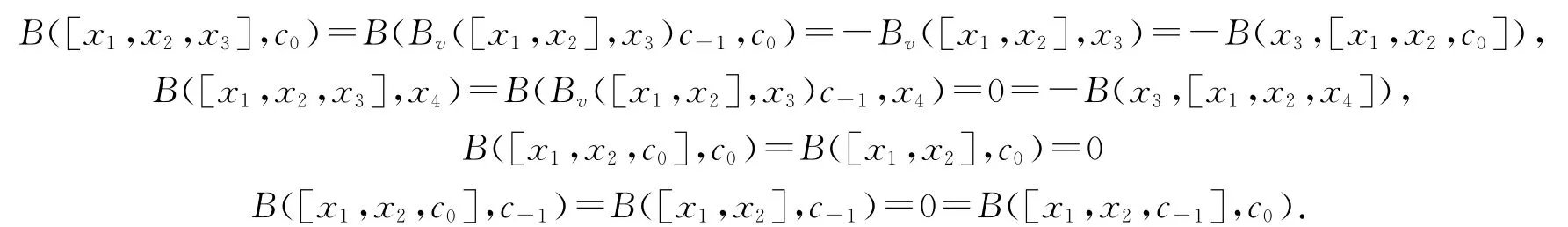
所以B 在3－李代数（G，［，，］）上满足式（3）.再由式（8）可知B 是非退化的，因此（G，［，，］B）是度量3－李代数，且对任意x，y∈V，B（x，y）＝Bv（x，y）.

对一个具有迷向中心的度量李代数与度量3－李代数，极大迷向中心在其代数结构的物理应用中有着重要意义.定理3告诉我们，由具有迷向中心的度量李代数可以得到具有迷向中心的3－李代数.

定理4 设（V，［，］，Bv）是域F 上非Abel的具有非零的迷向中心Z（V）的m－维度量李代数，f∈V＊满足f≠0，f（V1）＝0.设（G＝V+Fc0+Fc－1，［，，］，B）是定理3中的（m＋2）－维度量3－李代数，其中c0，c－1∈／V，那么Z（G）＝Z（V）+Fc－1，且Z（G）是迷向的.

证明 因为度量李代数（V，［，］，Bv）具有迷向中心Z（V），由文献［7］引理2.3可知，Z（V）⊆V1.因此f（Z（V））＝0.任取z∈Z（V），及∀x，y∈V，［z，x］＝［z，y］＝0，由式（7）可得，

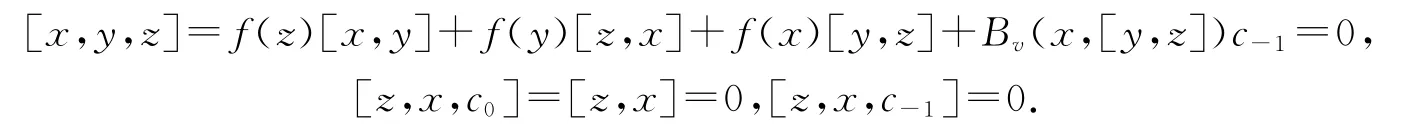
所以Z（V）⊆Z（G）.又对任意的q＝ω＋λc0＋μc－1∈Z（G），ω∈V，以及任意的x，y∈V，有

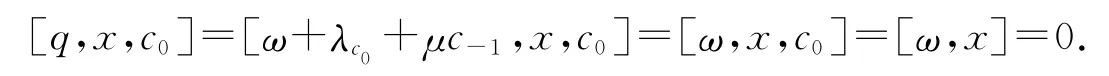
由x 的任意性，ω∈Z（V）.由［q，x，y］＝［ω＋λc0＋μc－1，x，y］＝λ［x，y］＝0及（V，［，］）是非Abel的李代数，得到λ＝0，所以q＝ω＋μc－1，即Z（G）⊆Z（V）+Fc－1.因此，Z（G）＝Z（V）+Fc－1.又由式（7）可知，B（Z（G），Z（G））＝0，所以Z（G）是迷向的.

［1］ FILIPPOV V.N－Lie algebras［J］.Sib Mat Zh，1985，26（6）：126－140.

［2］ NAMBU Y.Generalized hamiltonian dynamics［J］.Phys Rev，1973，D7：2405－2412.

［3］ TAKHATJAN L.On foundatiuon of the generalized Nambu mechanics［J］.Comm Math Phys，1994，160（2）：295－315.

［4］ LING W.On the structure of n－Lie algebras［D］.Siegn，University－GHS－Siegen，1993.

［5］ DZHUMADIL'DAEVAB A.N－Lie property of the Jacobian as a condition for complete integrability［J］.Sibirsk Mat Zh，2006，47（4）：780－790.

［6］ BAI Ruipu，HAN Wenqiang，BAI Chengming.The generation index of an n－Lie algebra［J］.J Phys A：Math Theor，2011，44：185201.

［7］ BAI Ruipu，WU Wanqing，LI Zhenheng.Some results on metric n－Lie algebras［J］.Acta Math Sin，2012，28（6）：1209－1220.

［8］ BAI Ruipu，BAI Chengming，WANG Jinxiu.Realizations of 3－Lie algebras［J］.J Math Phys，2010，51（6）：063505.

［9］ 贾培佩，赵雪婷，张泰.限制完满李三系［J］.河北大学学报：自然科学版，2012，32（3）：230－233.JIA Peipei，ZHAO Xueting，ZHANG Tai.On perfact restricted Lie triple systems［J］.Journal of Hebei University：Natural Science Edition，2012，32（3）：230－233.