基于Winger-SVD的轴承故障诊断方法
2014-07-24秦洪懋孙嘉兵孙宁
秦洪懋 ,孙嘉兵,孙宁
(1.浙江农业商贸职业学院,浙江 绍兴 312000;2.东北电力大学 自动化工程学院,吉林 吉林 132012)
当滚动轴承出现故障时,振动信号往往表现出非平稳的波动特征,且包含大量的工况信息,利用采集的振动信号对轴承故障进行分析的主要方法为时间和频率的联合分析方法,即同时提取振动信号时域和频域的局部信息。
小波变换[1-2]具有多分辨率的特性,在故障诊断领域应用较为广泛,但小波基函数选择是小波分析的一个难题。Winger分布作为时频分析的工具,有着简单的形式和明确的物理意义,在非平稳信号分析领域应用广泛,但存在频率混叠和虚假频率的现象,使得其时频信息并不能十分准确地刻画信号时频域局部信息的特征,应用也受到一定的限制。文献[3]提出了一种基于经验模态分解的振动信号Winger分布分析,虽然取得了抑制频率混叠和虚假频率的效果,却降低了时频谱的分辨率,抑制了有用的时频信息。
因此,提出了将Winger分布与奇异值分解相结合的特征提取方法,在得到表征信号完整时间频率分布的Winger时频谱后,用奇异值分解方法将Winger时频谱进行分解,得到的奇异值均值可以作为轴承故障诊断的特征,并使用支持向量机进行分类,对该方法的有效性进行了验证。
1 基本理论
1.1 Winger分布
振动信号往往具有非平稳性,信号时间和频率的联合分布称为信号的时频表示,Winger分布[4]是一种进行时频分析的工具,对于时域信号f(t),通过Fourier变换变成F(ω),Winger分布的定义为
(1)
ejtθdθ,
(2)
式中:t,τ为时间;ω为角频率;f(t)为时域信号;f*(t)为f(t)共轭复数;F(ω)为信号f(t)的Fourier表达式;F*(ω)为F(ω)的共轭复数;θ为相位。
Winger谱满足能量积分
(3)
(4)
式中:ω(t,ω)为t时刻、ω频率上的能量分布密度。因此,Winger谱是时域信号在时间和频率平面上的能量分布,具有明确的物理意义。
1.2 奇异值分解
奇异值分解[5]是一种重要的矩阵分解,主要优点是经过分解后的奇异值稳定性能好,即矩阵中的某些元素发生变化时,其奇异值变化不明显。此外,还具备旋转不变形与比例不变形的特性。
对于矩阵A∈Rm×n,存在正交矩阵
U=[u1,u2,…,um]∈Rm×m,
(5)
V=[v1,v2,…,vn]∈Rn×n,
(6)
使得UTAV=diag[σ1,σ2,…,σp]=S,即
A=USVT,
(7)
则(7)式为矩阵A的奇异值分解。其中σ1≥σ2≥…≥σp≥0,σi(i=1,2,…,p),U和V分别为A的奇异向量。
2 轴承信号的Winger谱分析
试验轴承型号为SKF6205-2RS,轴承内径25.001 2 mm,外径51.998 9 mm,球组节圆直径39.039 8 mm,钢球直径15.001 2 mm,电动机转速1 797 r/min,振动传感器安装在轴承基础端的机架上,采样频率为12 000 Hz,故障数据的采样时间长度为0.25 s,轴承振动信号如图1所示。
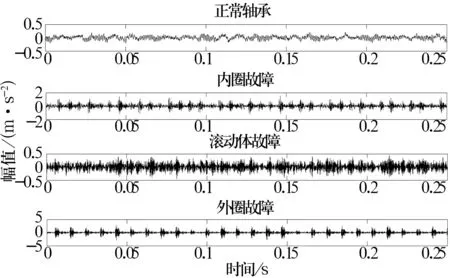
图1 轴承原始振动信号
对轴承原始振动信号进行Winger分布分析,得到4种工况下的Winger时频谱,频率分布范围为0~1 200 Hz。由图2可知,Winger谱中包含了丰富的时频信息,但存在频率混叠和干扰现象,并不能准确刻画信号时频域局部信息的特征。

图2 不同故障状态下轴承信号的Winger谱
由于故障振动信号Winger谱时频矩阵的维数较高,包含的数据量大,不利于后续分析,因此对振动信号的Winger时频谱进行奇异值分解,并将前50个奇异值作为特征值序列[6],结果如图3所示。由图3可知,轴承不同状态下的Winger谱奇异值亦不相同,其中故障时的奇异值比正常情况下的奇异值偏大,而且外圈故障时的奇异值明显增大。由于故障状态下Winger谱中包含了丰富的故障信息,并且奇异值分解具有良好的稳定性,将该方法用于特征提取,具有稳定性好、故障分类效果明显的特点。

图3 不同故障状态下信号的Winger谱奇异值
3 应用分析
振动数据来自文献[7],数据集的选择参考文献[8]中叙述的方法,故障类型有内圈、外圈及钢球故障。采样频率为12 000 Hz,轴承的损伤状况为单一损伤,通过电火花机分别在轴承内圈、外圈和钢球上加工制成,损伤的直径(盲孔直径)分别为177.8 μm(0.007 in),355.6 μm(0.14 in)及533.4 μm(0.021 in)。
数据集详情见表1,例如D070707代表3种故障状态的盲孔直径均为177.8 μm。 DINN,DOUT和DBALL分别为内圈、外圈和钢球故障数据集,分别包含了3种故障不同损伤程度的故障状态,用于评价该方法对故障损伤程度的评估能力。

表1 数据集
轴承正常状态的样本数为59,随机选取29个作为训练样本集,其余30个作为测试样本集;其他3种故障的样本数均为29,随机选择14个作为训练样本集,其余15个作为测试样本集。
支持向量机是基于统计理论发展的分类学习方法,在小样本和非线性的情况下,支持向量机的模式分类效果明显,因此,选择支持向量机作为故障诊断分类器,用来验证上述方法的有效性。选用Gauss核函数[7]形式,使用“一对一”的多类别识别方法,Gauss核函数形式为
(8)
式中:σ′为控制核函数高宽的参数,对于线性不可分情况引入惩罚因子C控制错误分类,σ′取值为1,C=100。
Winger谱奇异值作为故障特征,应用前20个奇异值作为输入向量,将表1的数据集进行训练与识别,分类结果见表2,从中可以看出,在所有的故障数据集中都取得相对满意的识别效果,说明该方法可有效诊断轴承故障。

表2 故障分类正确率
4 结束语
对比多种故障诊断方法,以分辨率和有效信息率为指标,提出了基于振动信号Winger-SVD的轴承故障诊断方法,能充分挖掘时频谱的有效故障信息。通过支持向量机的故障分类试验表明,基于Winger-SVD的轴承故障诊断方法对3种故障类型均有较高的识别率,可满足大型旋转机械在线诊断的要求,具有一定的实际应用价值。
