基于机电耦合的数控铣滚齿复合加工动力学仿真
2014-07-24许东海刘艺
许东海,刘艺
(1.洛阳轴承研究所有限公司,河南 洛阳 471039;2.总装备部装甲兵驻沈阳地区军事代表室,沈阳 110000)
转盘轴承是一种具有特殊用途的大型专用轴承,广泛应用于各种工程机械、起重机械和设备平台等。齿加工是影响转盘轴承生产效率的重要环节,数控铣滚齿复合机床有别于传统滚插齿机床,综合加工效率是传统滚插齿加工效率的4~6倍[1]。机电耦合动力学将电磁学与力学联系起来,形成交叉学科[2],其基础理论研究包含3方面的问题:如何正确建立机电耦合系统的数学模型;描述机电耦合系统的非线性数学方程组的研究方法;机电耦合系统的稳定性理论[3]。应用计算机建模和仿真技术可以在研制物理样机前得到数控机床的动力学特性,并为机械与电气参数的匹配、元器件的选型提供理论依据。
传统的建模法是运用已知定理、定律建立系统的简易数学模型。这种方法对于简单的耦合系统比较适用[4],但数控机床机电耦合系统是跨学科的非线性系统,简化的数学建模不能反映其真实情况。近年来,随着计算机技术的发展,多物理场及多学科设计优化技术逐渐得到应用[5],文献[6]较系统地阐述了多物理场耦合模型的建立以及数值模拟方法;文献[7]将多场耦合成功应用在隧道工程分析中,方便了复杂耦合系统的分析。同时,机电耦合相关建模和仿真软件的产生和应用方便了复杂机电系统的分析。德国ITI公司的SimulationX[8]和瑞典COMSOL 公司的MULTIPHYSICS[9]均是多学科、多物理场建模和仿真分析的CAE工具,涉及机、电、液、气、电磁等各个领域。
1 机械系统
数控铣滚齿复合机床结构如图1所示,包括1个主轴运动和3个进给运动。齿加工时水平进给系统固定,垂直进给系统和回转进给系统由数控系统联动控制,实现大模数齿轮的铣削和滚削。下文以垂直进给传动为例进行分析,如图2所示。垂直进给系统采用丝杠螺母传动,由交流伺服电动机驱动,在ADAMS中建立机电耦合系统的机械动力学模块。

图1 数控铣滚齿复合机床结构示意图

1—丝杠;2—主轴箱;3—刀具;4—待加工齿轮;5—转台
文献[10]对数控伺服系统进行了三环整定,但没有考虑机械系统及切削载荷对机电耦合系统的影响。铣齿加工为非连续性强力切削,瞬态切削载荷的影响因素复杂且变化幅值大,所以对机电耦合系统的快速响应性以及稳定性要求更高。文献[11]总结了铣齿切削功率的计算方法,在此基础上综合考虑铣齿加工周期和瞬时铣削深度的铣齿切削载荷进给分量模型Fz(t)为
ap=k+htan 20°,
式中:kp为铣削功率修正系数;d0为铣刀直径;ae为铣削深度;t为时间;af为每齿进给量;ap为铣削宽度;z为铣刀刀片数;n0为铣刀转速;k为盘铣刀顶部宽度;h为全齿高。
文中铣齿切削模型的切削参数为:铣刀模数m=16 mm,铣刀直径d0=400 mm,铣刀刀片数z=36,3个刀片为1组,主轴转速为80 r/min,进给速度v=120 mm/min,被加工齿轮材料为50Mn。铣齿切削为周期性载荷,其周期为
铣齿切削载荷产生的附加扭矩直接作用于丝杠,对机电耦合系统产生干扰。将铣齿切削载荷模型表示为阶跃函数和锯齿波函数,铣齿切削载荷转化为对应的丝杠扭矩,如图3所示。
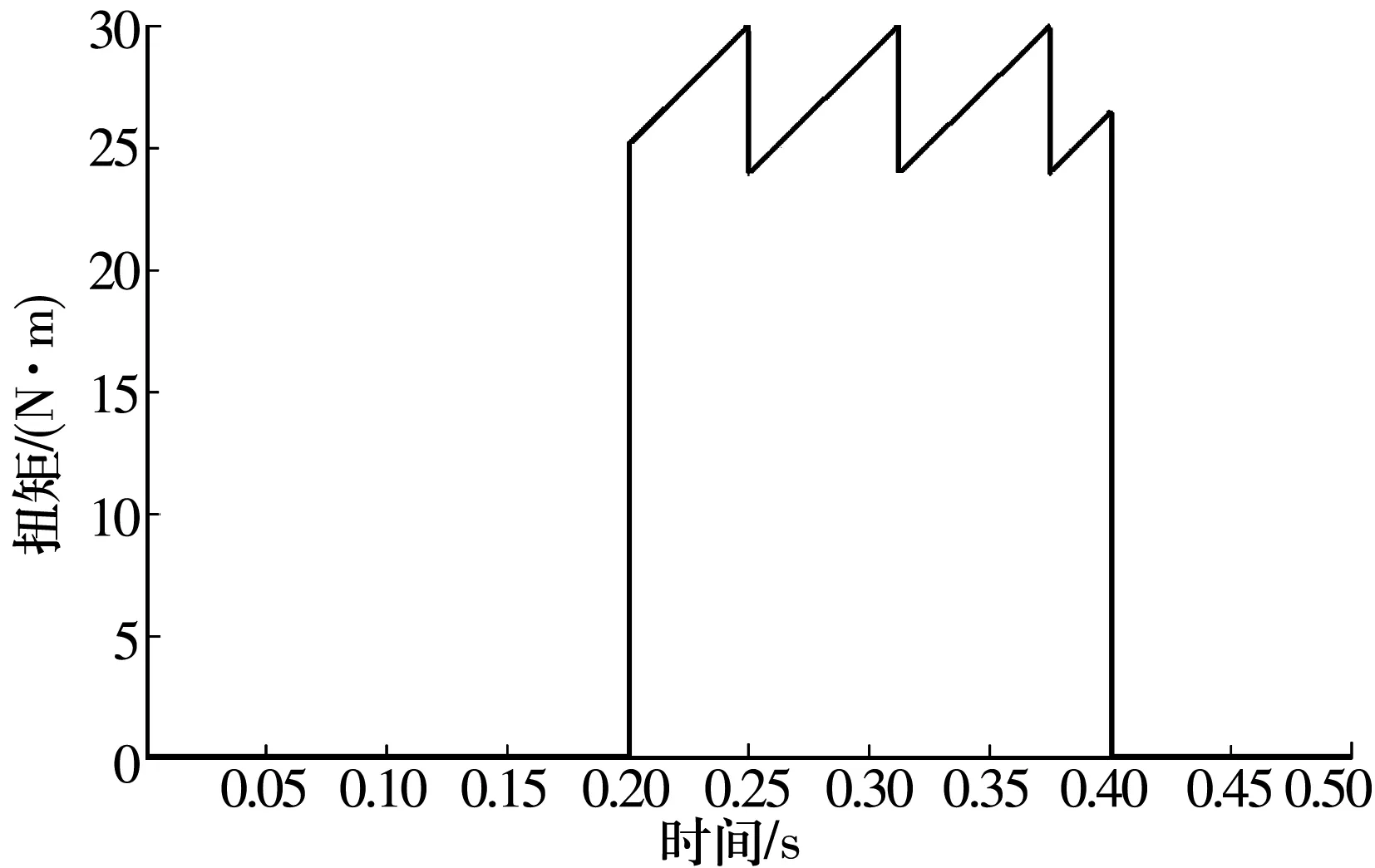
图3 铣齿切削载荷模型
2 控制系统
数控铣滚齿复合机床进给伺服系统采用半闭环控制方式,机电耦合关系如图4所示。该控制系统为轮廓控制,要求伺服系统既要能够精确定位,还要能够随时控制电动机的转速和转向。三相永磁同步伺服电动机(PMSM)常用的控制方法有:矢量控制、直接转矩控制、模糊控制、神经网络控制、鲁棒控制、自抗扰控制和复合控制等[12]。交流伺服电动机的位置控制是对磁场进行矢量变换控制,由电流环、速度环和位置环组成,在MATLAB/Simulink中建立包含伺服电动机的垂直进给伺服系统控制模型[13]。由于机械传递环节对控制系统有很大影响,必须重新整定系统三环控制的PID参数,垂直进给伺服系统半闭环机电耦合模型如图5所示。

图4 半闭环伺服系统机电耦合框图

图5 半闭环伺服系统机电耦合模型
3 机电耦合动力学模型及仿真分析
在MATLAB/Simulink中对机电耦合系统的三环响应进行仿真,并以机电耦合系统的单位阶跃响应评价其动态性能。实际工况采用匀加减速、S曲线加减速等控制方式,动态性能更优。系统采用1FK7101西门子交流伺服电动机进行驱动,行星减速器的减速比为1∶28,滚珠丝杠螺距为12 mm。在CAXA中建立垂直进给系统的三维实体模型(图6),通过IGES标准数据接口导入到ADAMS/View中。

图6 垂直进给系统的机械模型
在ADAMS/View中建立运动副约束:立柱通过固定副与大地相连;行星减速器、轴承座通过固定副与立柱相连;电动机与丝杠通过旋转副与大地相连,并建立耦合副,耦合转速比28∶1;丝杠通过螺旋副与丝杠座相连,设置导程为12 mm;丝杠座通过固定副与拖板相连;拖板通过移动副与立柱相连,设置滑动静摩擦因数为0.2,动摩擦因数为0.1,最后为电动机添加旋转驱动。在运动学仿真模型上添加驱动力矩,建立系统动力学仿真模型。
3.1 无机械环节的伺服系统仿真
在不考虑机械环节的情况下,使用无量纲单位阶跃函数作为系统输入,分析电流环、速度环和位置环的动态响应特性,仿真结果如图7所示。
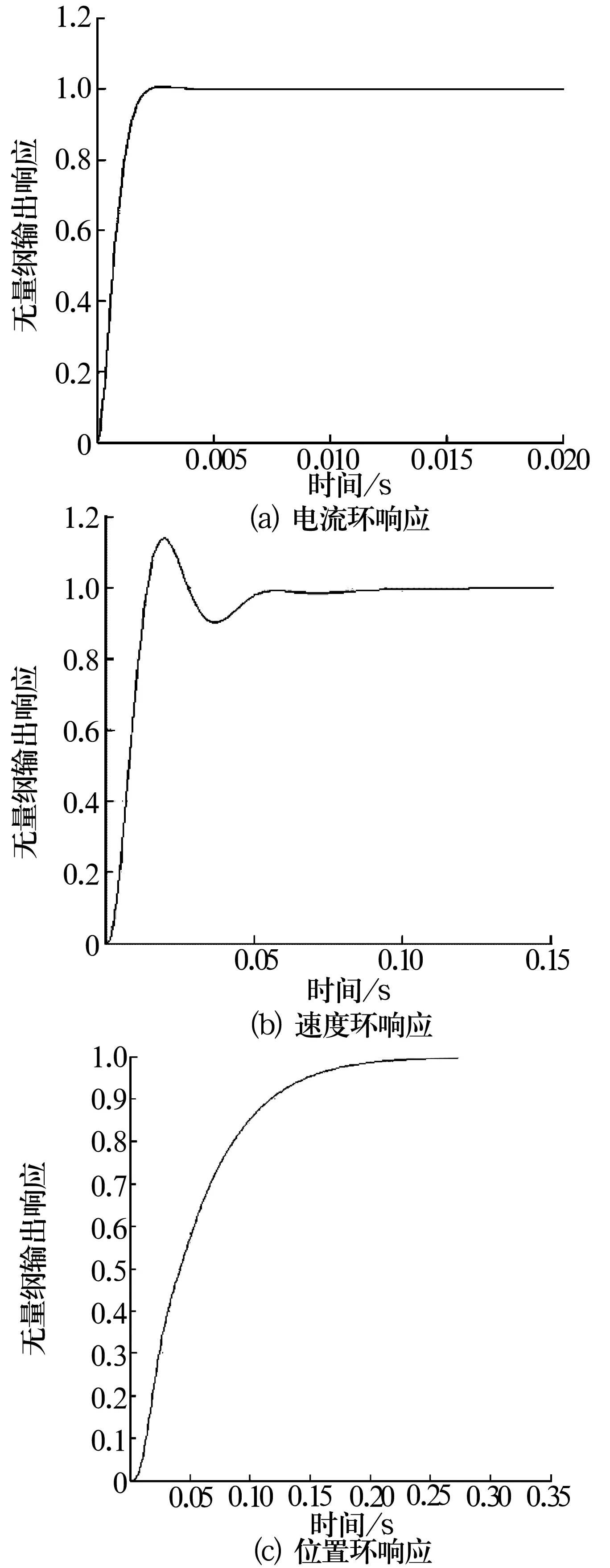
图7 单位阶跃函数的仿真结果
系统仿真结果见表1,电流环的响应速度快,位置环无超调量和稳态误差,而速度环超调量较大(13.2%)。实际应用中,数控系统采用的各种加减速控制能够大大降低超调量,因而机电耦合系统的动态响应稳定性能够得到保证。

表1 系统仿真性能表
3.2 伺服系统半闭环机电耦合仿真
在考虑垂直进给机械部分的情况下,按照图5所示机电耦合模型进行仿真。输入信号为电动机角位移1 rad的阶跃函数,输出信号包括电动机的角位移(图8a)以及主轴箱的直线位移(图8b~图8d)。

图8 半闭环机电耦合仿真结果
由仿真结果可知,伺服系统无超调量且稳定性较好。由图8a和图7c可知,伺服电动机角位移输出抵抗切削载荷冲击的能力较强;由图8a和图8c可知,稳态误差是由机械系统引起的,当载荷在0.4 s撤掉时,稳态误差可以消除;由图8b可知,无载荷时主轴箱位移环调节时间为0.3 s,无超调量,但存在一定的位移波动;由图8b和图8c可知,切削载荷的冲击会加大主轴箱位移的谐振,谐振频率为垂直进给系统机械系统固有频率(92.7 Hz),且会产生稳态误差;由图8d可知,反向间隙会在电动机启动瞬间给系统一个冲击,可以用阶跃函数模拟冲击载荷,反向间隙在数控系统中可以补偿,但会引起系统的振荡,由于其能够很快稳定下来,铣滚齿加工时,伺服进给系统已经稳定,影响较小。此外,周期性铣齿切削载荷的频率对主轴箱位移环的谐振并无太大影响,因为铣齿切削载荷的频率为16 Hz,远低于机械系统的固有频率。
4 结论
(1) 对数控铣滚齿复合机床垂直进给伺服系统的三环PID控制器参数进行整定,利用ADAMS和MATLAB建立机电耦合动力学模型,仿真结果表明采用三环PID控制的伺服驱动系统具有准确性、快速性和稳定性。
(2) 数控机床的机械部分对机电耦合系统的动态性能影响较大。铣齿切削周期性载荷会加大垂直进给伺服系统位置环的谐振并产生稳态误差,谐振频率为机械系统的固有频率。
(3) 由于机械系统刚性及切削载荷的扰动,需要采用鲁棒性更强的智能控制器。选用PID控制获得的参数值作为初始值,可以减少由于随意选取初值带来的系统不稳定问题,缩短智能算法和寻优时间。
