基于ADAMS的小型挖掘机转盘轴承的摩擦力矩分析

史丽晨，杜小渊，郭刚涛，赵力

(西安建筑科技大学 机电学院，西安 710055)

转盘轴承是一种可以同时承受较大轴向、径向载荷和倾覆力矩的大型轴承，在机械行业应用十分广泛,其摩擦力矩直接影响转盘轴承的使用寿命和工作状态。目前,国内外大多使用ADAMS对高速重载下的滚动轴承进行仿真分析，而对低速重载下的仿真分析，尤其是对转盘轴承摩擦力矩的动力学仿真研究很少。 因此，以某小型挖掘机的转盘轴承为研究对象，以Hertz接触理论为基础，采用Pro/E进行三维建模，使用ADAMS对转盘轴承进行摩擦力矩的动力学仿真。

1 接触分析理论

2个曲面物体相互接触挤压，接触部位的应力分布与接触面的形状、尺寸及表面粗糙度等许多因素有关。为使仿真结果更加可靠,根据Hertz接触载荷与变形的关系[1]，通过一系列的计算精确求解出刚度系数等重要仿真参数。

1.1 接触刚度系数的计算

研究对象为013.25.450型单排四点接触式内齿型转盘轴承，钢球直径为25 mm，球组节圆直径为450 mm，如图1所示。钢球与内、外圈的接触是典型的Hertz接触。在施加外载荷Q的情况下，实际接触面为椭圆形，如图2所示。

图1 小型挖掘机转盘轴承实物图

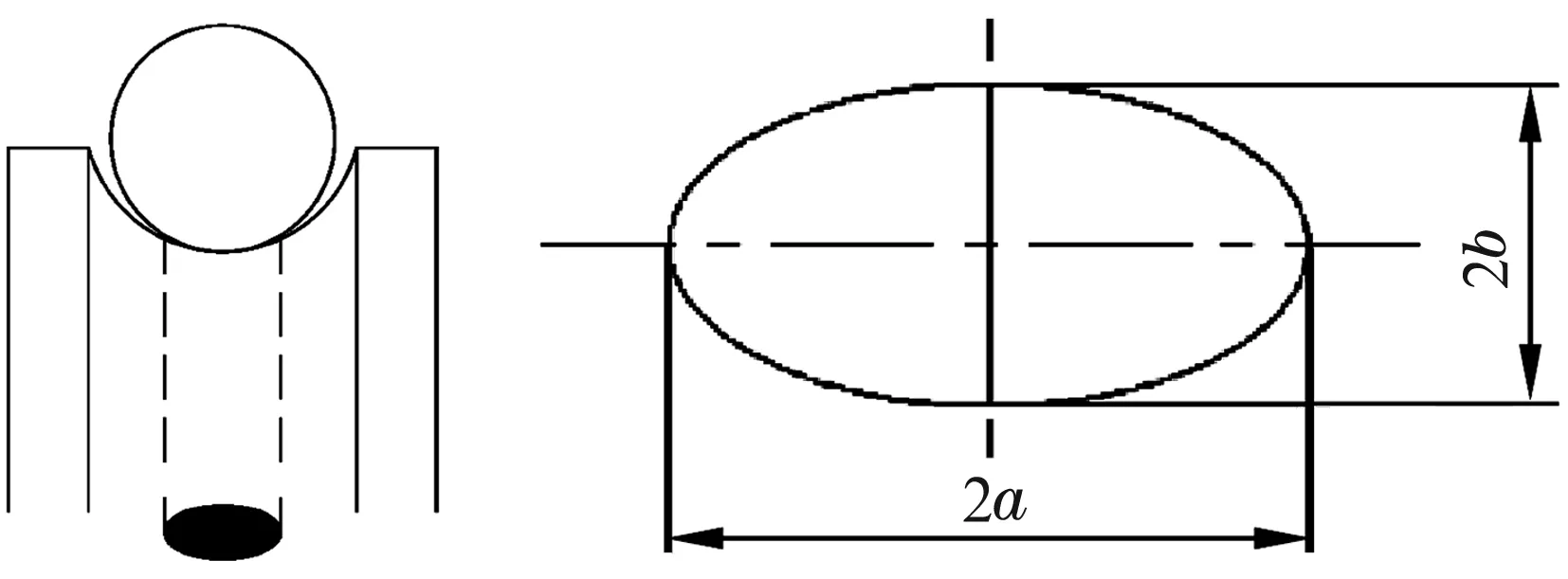
图2 钢球与沟道的接触面

转盘轴承内齿圈和外圈材料为50 Mn，钢球材料为GCr15，弹性模量E=207 GPa，泊松比ν=0.3。据Palmgren简化计算公式[2]可以得到接触面尺寸、接触变形量和刚度系数分别为

(1)

(2)

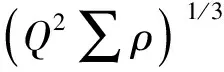
(3)

K=Q/δ2/3，

(4)

(5)

式中：ea，eb，eδ的值由主曲率函数F(ρ)通过Hertz接触系数表查出；主曲率之和∑ρ=ρⅠ1+ρⅠ2+ρⅡ1+ρⅡ2；ρ为接触表面曲率半径的倒数；下角标Ι,Π为钢球、沟道；1,2为转盘轴承的径向平面、轴向平面。

根据研究对象的尺寸，计算钢球与内、外圈的主曲率函数值[3]并查表得ea，eb，eδ的值，由(4)式计算得到钢球与内圈的接触刚度系数Ki=1.31×106N/mm，钢球与外圈的接触刚度系数Ke=1.33×106N/mm。

1.2 其他仿真参数的确定

除了接触刚度，摩擦因数μ也对摩擦力矩有着较大影响。对于重载或低速运转的轴承，可以采用Vogelphol摩擦因数公式[4]进行计算，即

μ/ψ=3/S0，

(6)

式中：ψ为相对间隙；S0为索氏数。经过计算可得摩擦因数μ=0.011,在ADAMS中进行仿真时取静摩擦因数、动摩擦因数与之相同，即Cst=Cdy=μ=0.011，其详细接触参数见表1。

表1 接触模型详细参数

2 转盘轴承摩擦力矩分析

转盘轴承的摩擦力矩可以分为2个部分，一部分是与载荷有关的摩擦力矩Mf；另一部分是与所受载荷无关的摩擦力矩M0。

2.1 与载荷有关的摩擦力矩

挖掘机在回转运动时，转盘轴承同时受到轴向载荷Fa、径向载荷Fr和倾覆力矩M的作用，其受力简图如图3所示。通常，径向载荷Fr相对于其他2种载荷影响很小，可忽略不计，分析时只考虑轴向载荷Fa和倾覆力矩M。采用载荷叠加法[5-6]计算转盘轴承滚道上的压力。

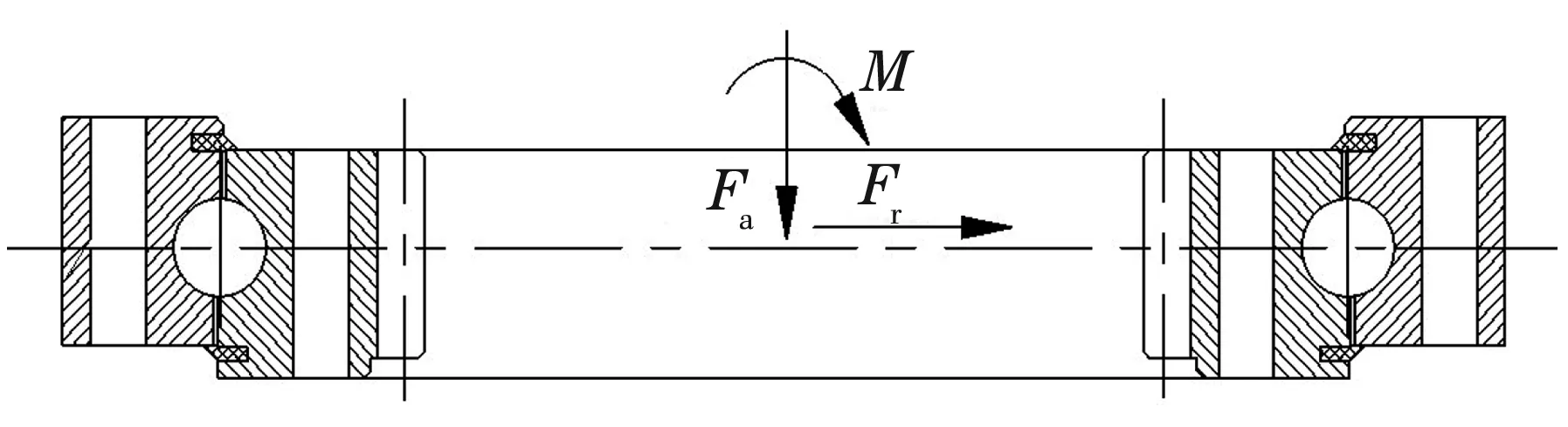
图3 转盘轴承受力简图

2.1.1 轴向载荷单独作用

在轴向载荷Fa单独作用时，沟道圆周上的压力分布是连续均匀的，根据力平衡条件可知滚道圆周上任意角φ处单位弧长上所产生的压力Qaφ为

Qaφ=Fa/(πDpwsinα)，

(7)

式中：α为钢球与沟道的接触角，α=45°；Dpw为球组节圆直径，Dpw=450 mm。

2.1.2 倾覆力矩单独作用

沟道上的最大单位压力QM0位于力矩M作用的平面内，如图4所示。沟道上其余部位任意角φ处所受的单位压力QMφ为最大单位压力QM0的cosφ倍, 则作用于某一微小弧ds上的压力对中心轴所产生的力矩为

(8)

根据力矩平衡条件可得

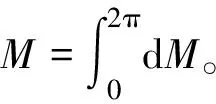
(9)

因此在倾覆力矩M作用下，在滚道圆周上任意角φ处的单位弧长上的压力为

(10)

图4 倾覆力矩作用下单位弧长压力图

2.1.3 轴向载荷和倾覆力矩耦合作用

轴向载荷Fa和倾覆力矩M在转盘轴承滚道上产生的压力方向在区间(-π/2，π/2)内相同，在区间(π/2，3π/2)内相反，故可以将2种压力叠加，如图5所示。因此，转盘轴承在轴向载荷Fa和倾覆力矩M耦合作用下, 滚道圆周上任意角φ处的单位弧长上的压力为

QaMφ=Qaφ+QMφ=

(11)

图5 压力叠加图

在轴向载荷Fa和倾覆力矩M的耦合作用下，转盘轴承的摩擦力矩为

(12)

式中：μ为转盘轴承钢球与滚道之间的摩擦因数；ds为单位弧长，ds=(Dpw/2)dφ。

将(7)～(11)式代入(12)式可得

8M|]，

(13)

式中：K为滚动体的形状系数，考虑转盘轴承滚动体形状不同对摩擦力矩所产生的影响而引入的参数。滚子K=1，钢球K=0.95。

2.2 与载荷无关的摩擦力矩

与载荷无关的因素有许多，主要考虑一些比较重要的因素，如润滑剂、密封等的影响。由于转盘轴承转速低且采用脂润滑橡胶圈密封，结构类型可按照角接触轴承进行处理[7-8]，即

(14)

式中：f0为与轴承润滑、密封方式有关的系数。

2.3 转盘轴承的摩擦力矩

在考虑与载荷有关和无关的情况之后，可得转盘轴承的摩擦力矩为

Mh=Mf+M0。

(15)

根据试验小型挖掘机转盘轴承的受力状况，取轴向载荷Fa=10 kN，倾覆力矩M=5 000 N·m，然后将各参数代入到(10)～ (12) 式，得到转盘轴承摩擦力矩的理论值Mh为92 831 N·mm。

3 转盘轴承的摩擦力矩仿真

在ADAMS中有2种接触碰撞的计算模型，一种是基于Hertz理论的Impact函数模型，一种是基于恢复系数(coefficient of restitution)的泊松模型。2种模型都来自于法向接触约束的惩罚函数。文中选用更加适合接触问题的Impact函数模型。

ADAMS中常用的积分器有2种，分别为GSTIFF积分器和WSTIFF积分器[9]，分别选用这2种积分器对转盘轴承进行动力学仿真，接触模型的仿真参数见表1。其他参数按系统默认值设置，仿真时间设置为1 s，仿真步数设置为50步。定义转盘轴承的速度为10.9 r/min，与挖掘机的回转参数保持一致，其他参数同理论计算部分一致，取轴向载荷Fa=10 000 N，倾覆力矩M=5 000 N·m。

2种积分器的仿真结果见表2。从表中可以看出，2种积分器的仿真结果与理论值都比较接近，但仿真值总比理论值小一些。这是因为仿真过程无法做到理论计算那样全面考虑，忽略了一些比较重要的因素，如润滑脂、密封等因素对转盘轴承摩擦力矩的影响。与此同时，通过仿真值与理论值的对比也可以说明通过ADAMS对转盘轴承进行仿真分析来求得摩擦力矩是基本可行的。

表2 2种积分器仿真数据

2种积分器求得的摩擦力矩如图6所示，可以看出，采用WSTIFF积分器时，不仅仿真值更加接近理论值，而且曲线的起伏更小，数据更加精确。但是采用WSTIFF积分器时往往仿真时间比较长，因而效率不高。所以，当分析数据对于精确性要求不高时，采用GSTIFF积分器是比较合适的选择。

图6 摩擦力矩对比图

4 结束语

通过对小型挖掘机转盘轴承进行接触动力分析得到其刚度系数等重要参数，并对其理论摩擦力矩进行计算；通过动力学分析软件ADAMS对其进行仿真分析，得到摩擦力矩的仿真值。通过摩擦力矩理论值与仿真值的对比，为摩擦力矩的研究提供一些参考，也为摩擦力矩的实际测量提供一些理论依据。同时，分别使用2种积分器对转盘轴承模型进行动力学仿真计算，得到2种积分器的分析结果和图形，更加直观地反映了2种积分器的优缺点，为ADAMS积分器的选择提供了参考。