谐波小波滤波与HHT在轴承故障诊断中的应用
2014-07-24臧怀刚王石云王冀龙
臧怀刚,王石云,王冀龙
(燕山大学 电气工程学院 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
滚动轴承在旋转机械中应用极为广泛,也是最易损坏的零部件[1],其工作状态直接影响机械设备的安全与性能。因此,对轴承的状态监测与早期故障诊断具有重要意义[2-3]。
谐波小波具有良好的盒形频谱特性,是一个理想的带通滤波器,可以将任何信号正交、无冗余、无泄漏地分解到相互独立的频段上[4]。通过谐波小波将特定频段的成分与信号的其他频率成分分解后分离,从而消除了其他频段成分对该频段的影响,使一些被淹没的较弱信号凸显出来,相当于提高了信噪比。为了研究信号某一特定频段的成分,对信号的谐波小波分解进行重构时,可将其他频段的谐波小波系数置为0,只保留该频段的小波系数。由于谐波小波的正交性,重构的结果只包含该频段的成分,剔除了其他成分,达到了滤波的目的[5]。
HHT(Hilbert-Huang Transformation)是一种整体变换,虽然不能反映信号的局部信息,但不受Fourier分析的局限,其应用经验模态分解(Empirical Mode Decomposition,EMD)理论将信号分解成相互独立的若干固有模态函数(Intrinsic Mode Function,IMF)的和,并对每个IMF进行Hilbert变换,得到信号的瞬时频率和幅值,能够精确描绘出信号的时频谱和幅值谱图,且具有自适应性,主要用于复杂、非平稳信号的时频局部分析[6-7]。在此,尝试将谐波小波滤波去噪与HHT结合,并应用到轴承故障诊断中。
1 算法
1.1 谐波小波原理
谐波小波是一种小波函数。在频带[m2π,n2π]内,定义函数的Fourier变换为[8-9]
(1)
时域表达式为
(2)
(2) 式称为广义谐波小波[10-11]。当m=1,n=2时为经典谐波小波,谐波小波实部为偶函数,虚部为奇函数。
连续时间信号x(t)的谐波小波变换定义为
(3)
对 (3) 式进行Fourier变换得
(4)
(3)和 (4) 式分别为信号x(t)的谐波小波变换在参数m,n尺度下的时域和频域表达式,其离散形式可写为
r=1,2,…,N-1。
(5)
1.2 HHT基本原理
Fourier频谱的幅值只能反映频率在信号中实际存在的可能性,而边际谱的幅值能真实反映频率在信号中是否存在。利用边际谱的线性性质进一步给出边际谱的物理意义,即边际谱的幅值表示信号在某一频率各个时刻的幅值之和。每个IMF是满足以下2个条件的信号:(1)整个信号中零点数与极点数相等或至多相差1;(2)信号上任意一点,由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为零,即信号关于时间轴局部对称[12]。
信号x(t)经过EMD处理后可以成为相互独立的若干IMF分量ci(t)(i=1,2,…,n)和1个残量rn(t)的线性组合
(6)
对(6)式中的每个本征模函数ci(t)进行Hilbert变换得
(7)
式中:P为柯西主分量。
构造解析信号
(8)
可以求出瞬时频率为
ωi(t)=dφi(t)/dt。
(9)
则
(10)
式中:Re表示取实部;ai(t),φi(t)为每个固有模态函数ci(t)经Hilbert变换后构造的解析信号的幅值函数和相位函数;此处省略了残量rn。
Hilbert谱为
(11)
Hilbert边际谱为

(12)
式中:T为信号总长度。当H(ω,t)或h(ω)中有某一频率的能量出现时,就表示一定有该频率的振动波出现,Hilbert边际谱能比较准确地反映信号的实际频率成分。
1.3 故障诊断流程
首先,对采集信号进行谐波小波去噪处理,去除噪声信号对轴承振动信号的干扰;然后,进行EMD处理,得到各个IMF分量;最后,对包含故障频率的IMF分量进行Hilbert边际谱分析,诊断出故障类型。故障诊断流程如图1所示。

图1 故障诊断流程图
2 应用分析
2.1 试验数据分析
以西储大学的SKF6205-2RS轴承故障数据为例[13],轴承转速为1 797 r/min,钢球数为9,钢球直径为7.94 mm,球组节圆直径为39.04 mm,计算得轴承内圈、外圈和滚动体故障特征频率分别为162,107和141 Hz。对采样频率12 kHz、采样点数2 400的轴承外圈故障信号进行分析,波形如图2所示。
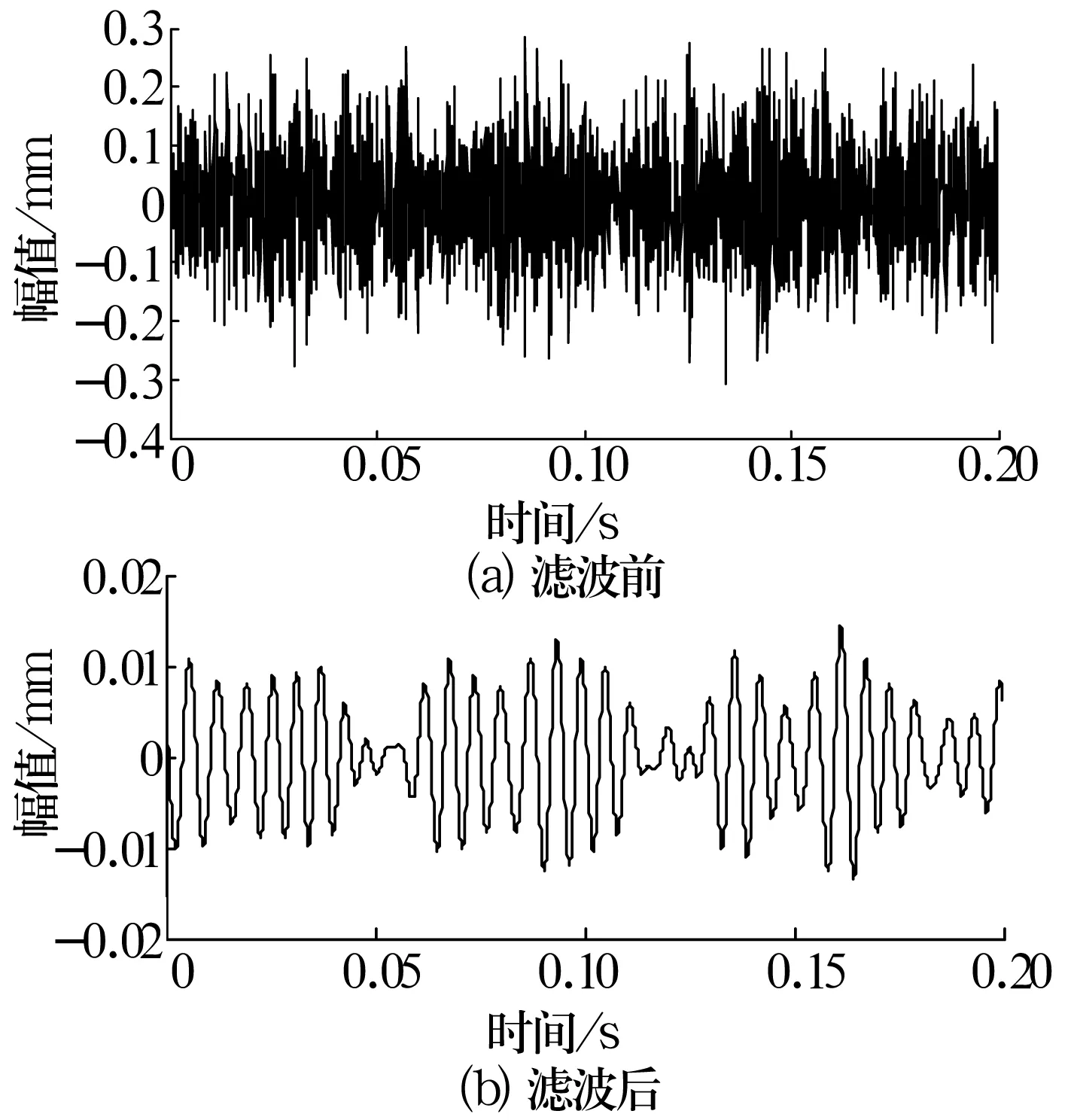
图2 外圈故障信号的时域波形
由图2a可以看出,轴承信号淹没在噪声中,无法识别故障类型;经过谐波小波滤波处理后,由图2b可以清楚地看出,谐波小波滤波器可有效消除干扰噪声,提高信噪比。图2b中的振动信号呈现有规律的波动,但仍然无法看出信号的故障特征频率。因此,对信号进行EMD处理,得到不同频率段的IMF分量如图3所示。通过分析发现IMF1分量中含有明显且均匀的冲击成分,其Hilbert谱如图4所示。

图3 滤波后经EMD处理的轴承信号
由图4可以看出,峰谱值为106.3 Hz,与试验轴承的外圈故障频率比较接近,可以判断轴承为外圈故障。
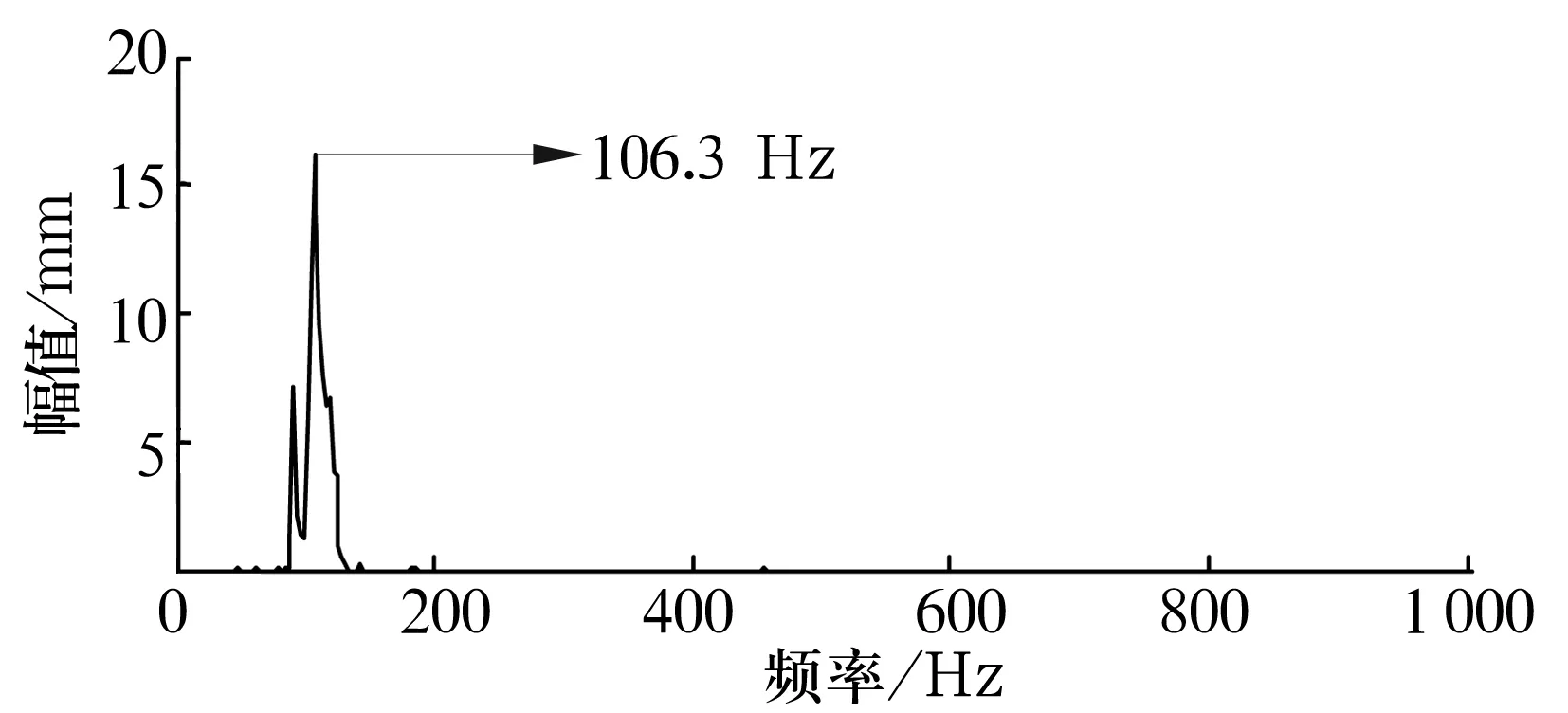
图4 IMF1的Hilbert边际谱
若不经谐波小波滤波,直接对信号进行EMD处理,并对包含故障频率的特征频率分量进行Hilbert谱分析,结果如图5所示。
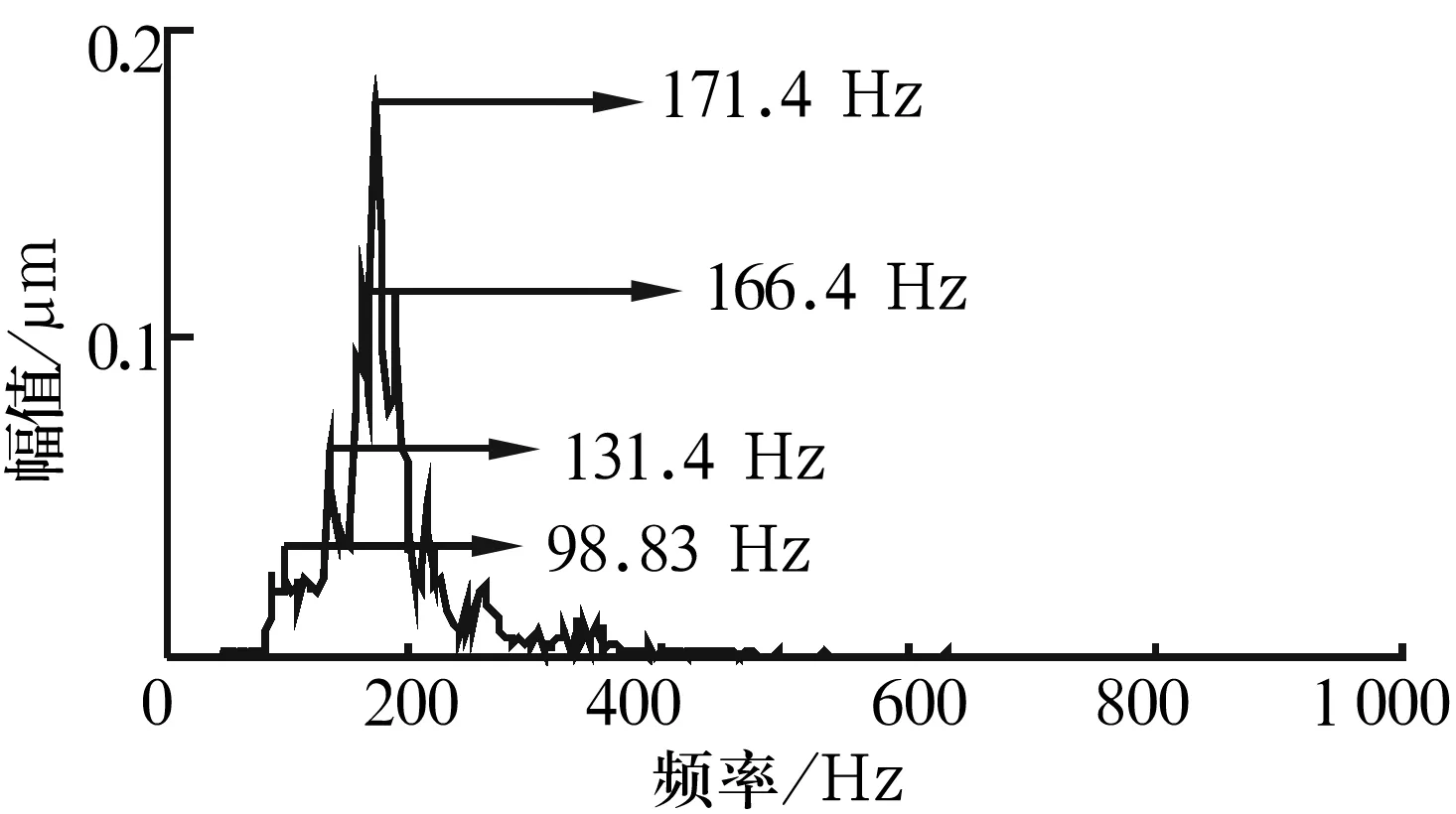
图5 未经谐波小波滤波信号的Hilbert边际谱
由图5可以看出,频率上升和下降阶段均呈阶梯形,出现了大量边频,给信号的物理解释带来困难,而且故障诊断受到干扰,容易引起误判。与图4比较可得,谐波小波滤波可以有效去除干扰频率,突出信号的主要成分。
2.2 实际应用
针对某变速箱中NU205M轴承实际信号进行分析。其中,轴承外圈有直径为0.403 mm、深度为0.223 mm的点蚀,控制器频率设置为40 Hz,振动信号由横向通道数据记录仪采集,采样频率为10 kHz,实际转速为1 188.12 r/min。计算可知轴承外圈故障频率为104 Hz,波形如图6所示。
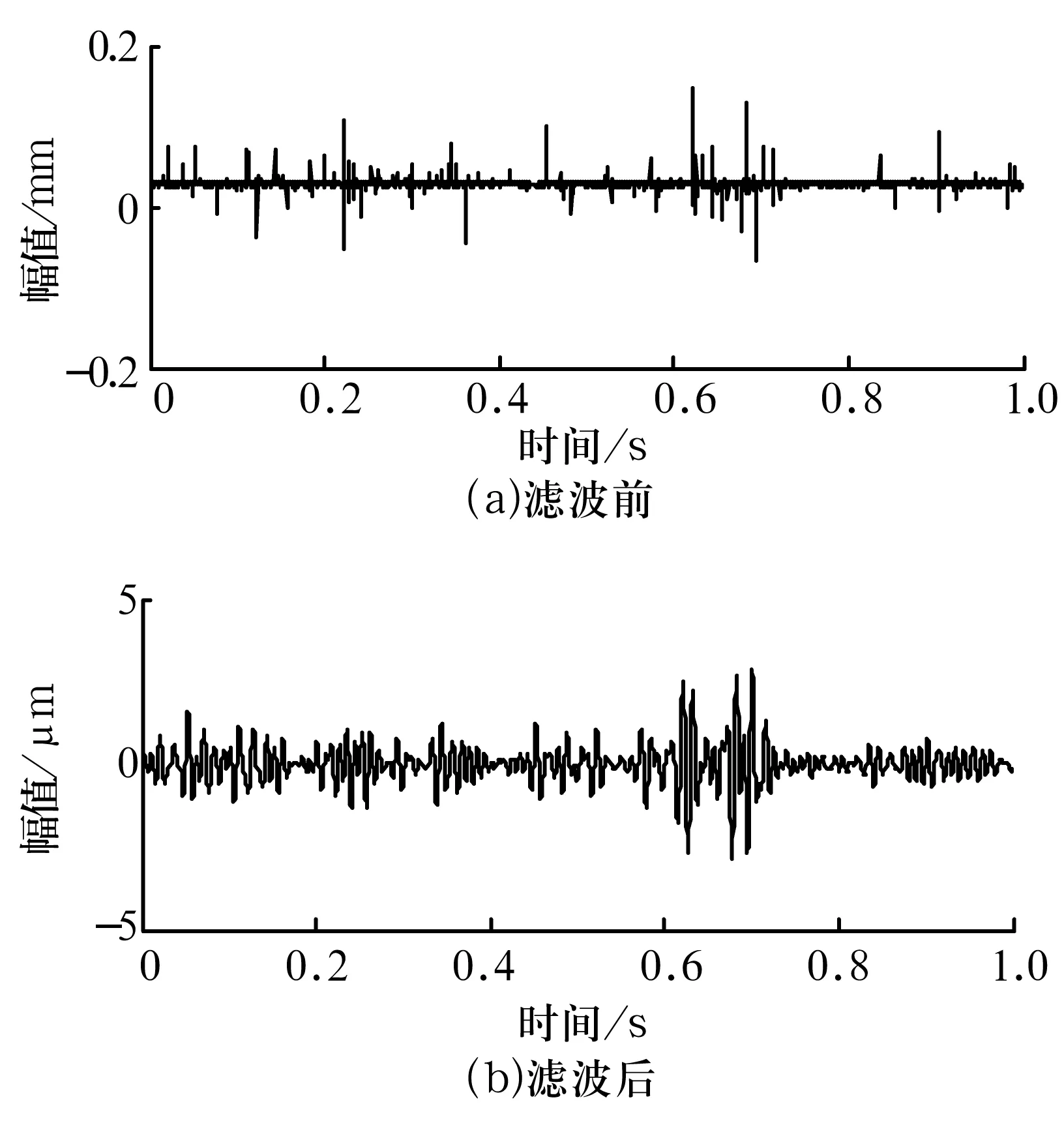
图6 实际外圈故障信号的时域波形
经过谐波小波滤波处理后,由图5b可以看出,谐波小波滤波器有效地消除了干扰噪声,提高了信噪比,图中的振动信号呈现有规律的波动。对滤波后的信号进行EMD处理,如图7所示。
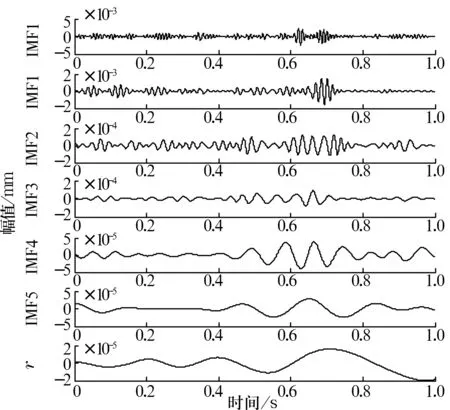
图7 EMD处理后的轴承信号
经谐波小波滤波处理后,对特定信号频率段IMF1进行边际谱分析,结果如图8所示。从图中可以清楚看出峰谱值为107.4 Hz,诊断为外圈故障,与实际情况相符。
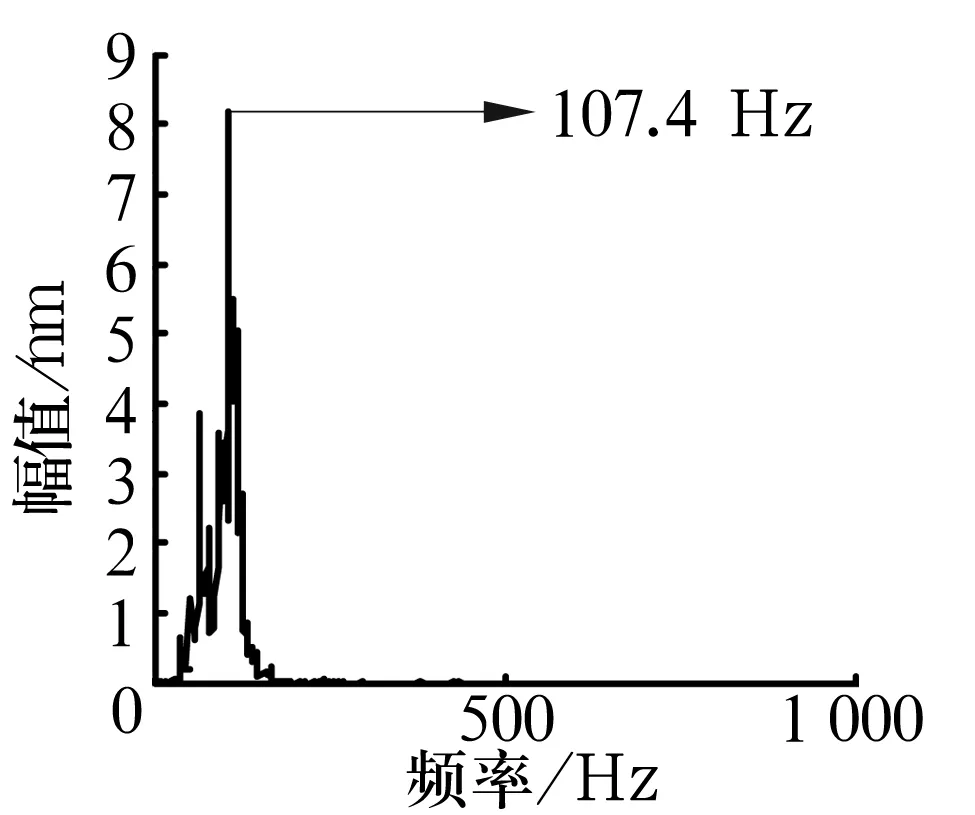
图8 外圈故障轴承Hilbert边际谱
另一NU205M轴承存在内圈故障,为直径0.32 mm、深0.217 mm的点蚀,控制器频率设置为20 Hz,振动信号由横向通道数据记录仪采集,采样频率为4 kHz,实际转速为589.68 r/min。计算可知轴承内圈故障频率为76.167 Hz。经谐波小波滤波处理后,对特定信号频率段作边际谱分析,结果如图9所示。从图中可以清楚看出峰谱值为74.8 Hz,诊断为内圈故障,与实际情况相符。
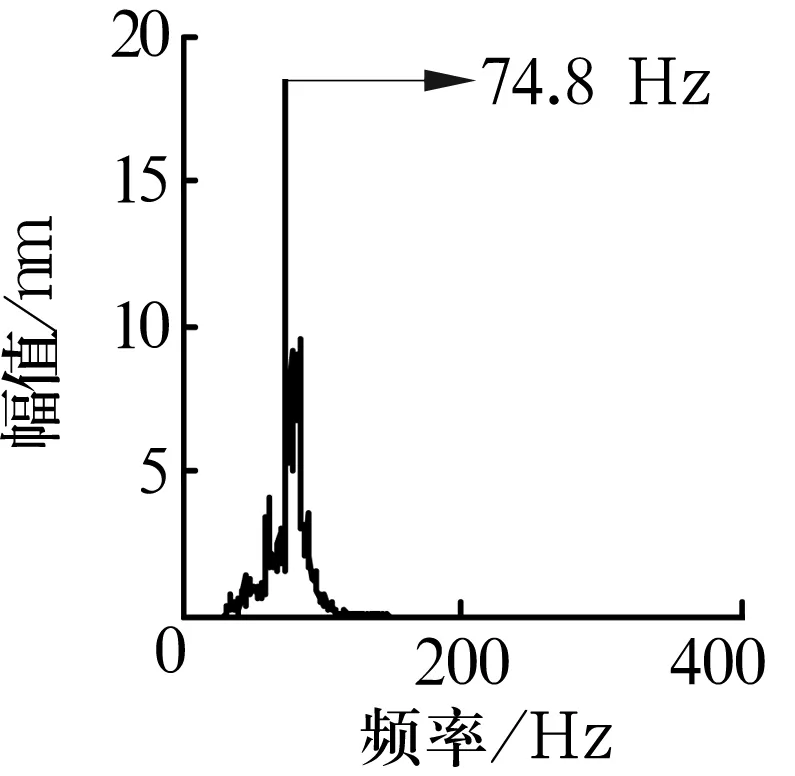
图9 内圈故障轴承Hilbert边际谱
3 结束语
将谐波小波滤波与HHT相结合,应用到滚动轴承故障诊断中,实例分析表明,该方法能有效去除干扰噪声,突出噪声环境下轴承振动信号的数据特征,进而提取故障信号的特征成分,具有实用价值。
