滚动轴承寿命的统计模拟
2014-07-24姜英硕姜祺周佳新汪东华
姜英硕,姜祺,周佳新,汪东华
(1.沈阳建筑大学,沈阳 110168;2.清华大学 工业工程系,北京 100084;3.中交煤气设计院有限公司, 沈阳 110026)
1 前言
拖拉机等工程运输车辆上使用的滚动轴承(以下简称轴承)通常有几套、几十套,甚至多达上百套,构成了轴承子系统。工作过程中任何一套轴承发生疲劳、磨损或永久变形等故障,均会导致轴承子系统乃至整台主机发生故障。因此,预测轴承可靠性指标,及时采取可能的措施提高轴承使用寿命是十分必要的。
目前轴承选型和寿命计算普遍采用ISO 281—2007和GB/T 6391—2010确定的滚动轴承额定寿命计算公式[1],经变换公式形式可得轴承额定寿命计算式为
(1)
式中:C为轴承额定动载荷,N;P为轴承当量动载荷,N;n为轴承工作转速,r/min;ε为寿命指数。
用(1)式可求出轴承可靠寿命L10的值。但应当注意的是,在拖拉机等工程运输车辆上,轴承载荷和转速实际上都是变量,变化幅度较大,且具有随机性。
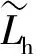
2 轴承载荷和转速的分布
现场试验和工作实际表明,拖拉机等工程运输车辆上的轴承载荷为随机变量,载荷峰值服从正态分布[2]。根据集材用拖拉机模拟工况下的轴承“载荷-时间历程”样本记录,用峰值计算法求得轴承载荷频谱[3-4],结果见表1。
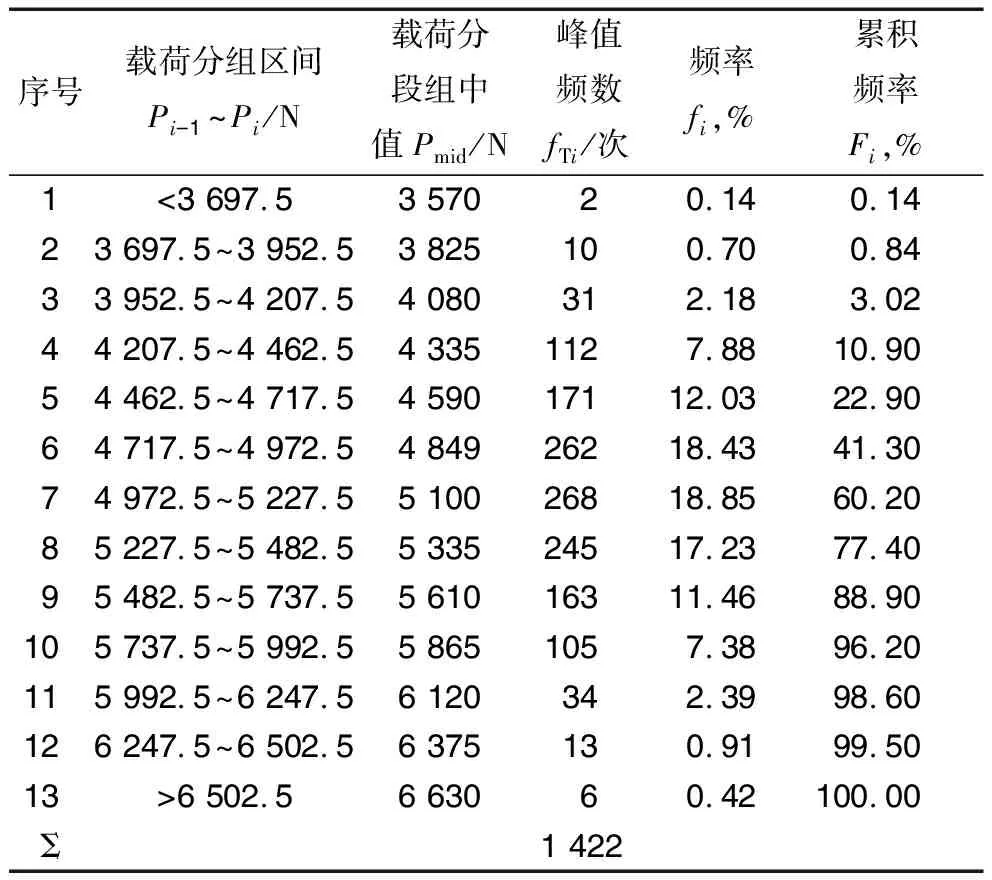
表1 集材用拖拉机轴承载荷频谱

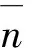

表2 及的正态分布参数
3 轴承寿命的统计模拟
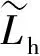
(1)用数学方法产生统计独立的(0,1)均匀分布的随机数序列{ri}N。
(2)用标准正态分布随机数抽样式,成对产生标准正态分布随机数序列{Zi}N,其抽样式为
(2)
式中:i=1,3,5,…,N。对于标准正态分布的分布参数,均值μ=0,均方差σ=1。
(3)利用线性变换,对轴承随机载荷和随机转速进行模拟,产生正态分布的随机数序列{Pi}N,{ni}N,其模拟式为
(3)
(4)
{Zi}NSP)ε],
(5)
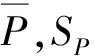
轴承参数主要有:型号为N210(圆柱滚子轴承),额定动载荷C=4.2×104N,依据GB/T 6391—2010取寿命指数ε=3.33。为保证模拟精度取样本容量N=2.2×103次,轴承载荷和转速的均值、均方差见表2。将各已知常数、随机变量和已知参数代入(5)式,通过编程计算,可得轴承寿命的随机数序列{Lhi}N。对寿命样本进行统计处理,并用χ2检验法对轴承寿命分布进行拟合度检验,结果见表3。
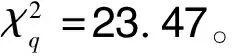
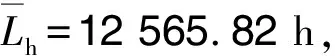
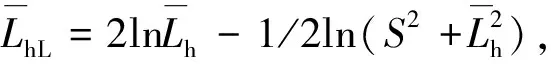
(6)
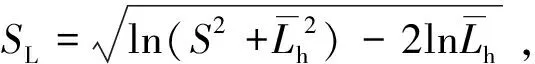
(7)
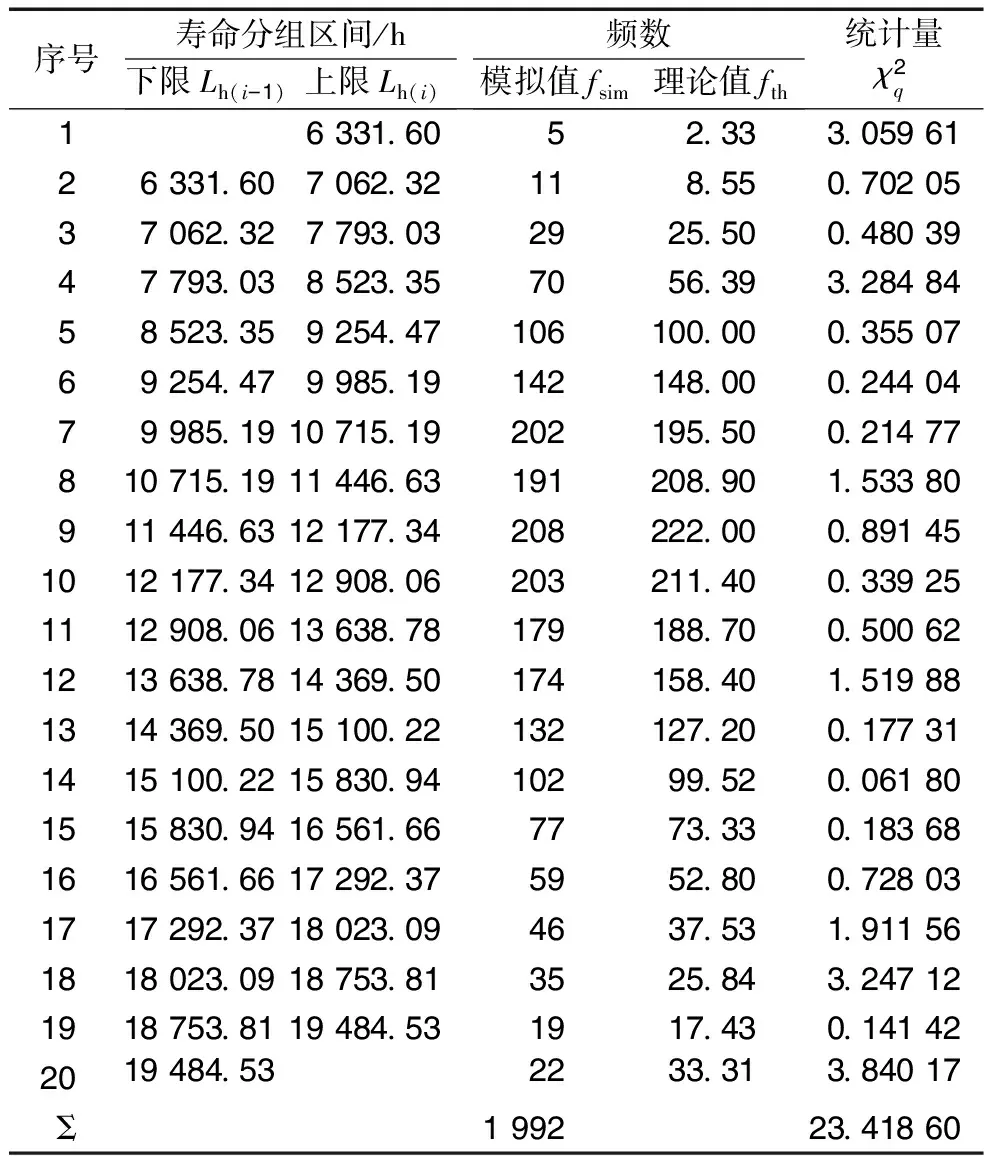
表3 轴承寿命分布的χ2检验结果
(5)用可靠性特征量计算公式[8]求取轴承可靠度R(L)、故障率λ(L)、可靠寿命L(R)及中值寿命L50等指标。
R(L)=1-Φ(Z)=
(8)
式中:Φ(Z)为标准正态分布函数,可查标准正态分布表。
(9)
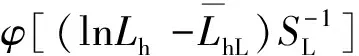
(10)
式中:ZP为标准正态分布分位点,可查标准正态分布表。
(11)
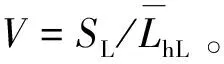
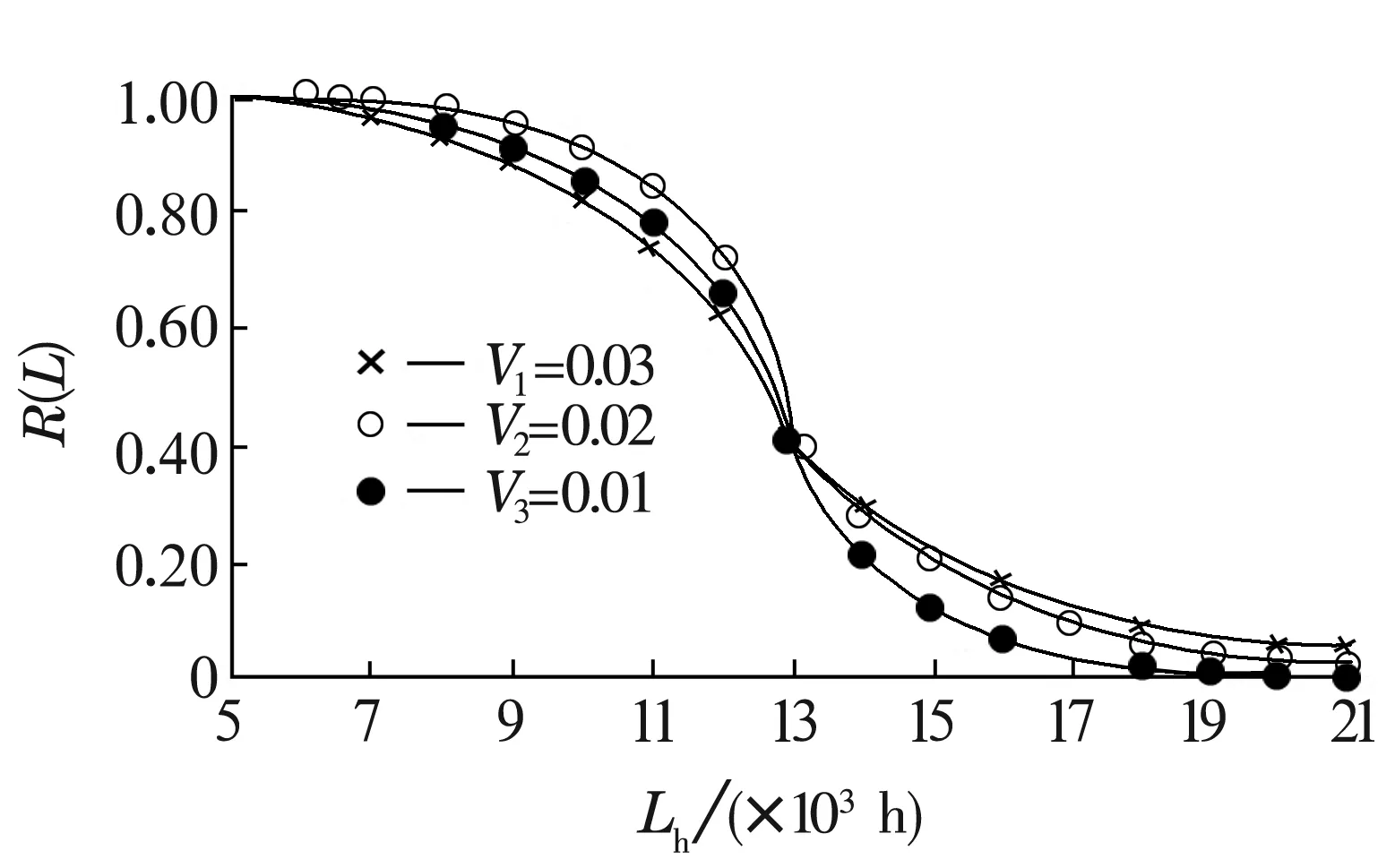
图1 轴承R(L)-Lh曲线
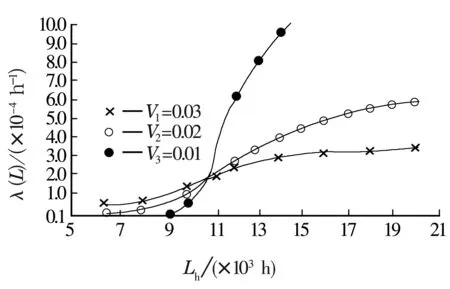
图2 轴承λ(L)-Lh曲线

表4 滚动轴承可靠性特征量
4 轴承统计模拟结果及分析
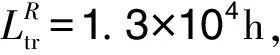
5 结论
(2)如果轴承随机载荷和随机转速服从正态分布,轴承寿命将服从对数正态分布。
(3)用统计模拟方法求取轴承寿命是可行的。模拟结果可作为预测轴承可靠度等指标和备件数量的依据。
