基于两点的时间序列相似性研究
2014-07-24刘永志
刘永志
1.南京航空航天大学 计算机科学与技术学院,江苏 南京 210016; 2.宣城职业技术学院 信息工程系,安徽 宣城 242000
基于两点的时间序列相似性研究
刘永志1,2
1.南京航空航天大学 计算机科学与技术学院,江苏 南京 210016; 2.宣城职业技术学院 信息工程系,安徽 宣城 242000
目前,时间序列相似性判定大多采用欧式距离和动态时间弯曲DTW(Dynamic Time Warping)方法,这两种方法均存在一定缺陷。欧式距离要求序列长度一样,垂直移动序列将影响相似性判定和阈值设置的经验性;动态弯曲距离对欧式距离进行了优化,避免了欧式长度的一致性,但其他两个缺点仍然存在且计算复杂度增加。提出了一种新的基于两点时间序列相似性算法,可计算任意两序列的相似度。首先分析了两点组成的序列形态,提出了相似性判定方法TPSS(Two Points Segmentation Similarity);其次为提高相似性判定的鲁棒性,减少人为阈值设置的影响,对TPSS进行了拓展;最后给出了算法及实验分析。实验结果表明,该算法能很好地判定任意序列的相似性,提高了鲁棒性及减少人为干预,对数据挖掘中的聚类与预测有很好的帮助作用。
时间序列;相似性;数据挖掘;比值序列
时间序列是按时间先后顺序排列的数据,并保存在介质上。它广泛存在于工业、农业及商业等领域,与人们生活息息相关[1-3],已引起研究者的广泛关注,起初在统计领域研究颇多,现在亦引起了数据挖掘领域的重视。
目前时间序列相似性研究方法主要有:基于形态的相似性、基于特征的相似性、基于模型的相似性、基于数据压缩的相似性。基于形态的相似性具有普遍性和实用性,在满足一定条件下可以取得与其他3类方法相近的度量结果。在研究形态的相似性方面,国内外学者取得了部分成果,比较有代表性的有Keogh等提出的分段累积近似PAA、分段线性表示PLR和符号集合近似SAX等方法[4-5]。在国内,梁建海等提出了斜率偏离的方法[6];张雪丽等提出基于角点相似性的方法[7];董晓莉等提出了七元模式组合法[8]。这些方法各有特点,为时间序列相似性研究提供了可以借鉴和参考的方向。
本研究在详细分析了两点组成的基本形态基础上,提出一种新的基于两点的时间序列相似性算法TPSS。依次连接相邻两点,组成最基本的平稳序列、上升序列及下降序列,利用基本序列判定定理判别是否相似。TPSS算法仅需一次扫描序列数据库,就可以比较等间隔时间序列的相似性,并根据TPSS算法对序列的相似性进行计数,输出相似度。此方法屏蔽掉了欧式距离的不能垂直移动、序列长度相同及阈值的人为性等缺点,在运算效率上优于DTW,并克服了DTW阈值的人为性。
1 时间序列
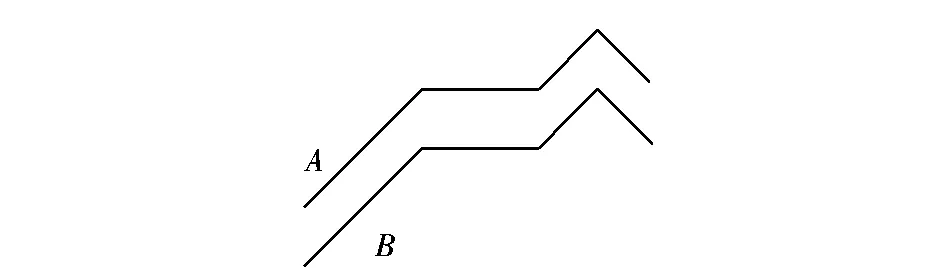
按照时间先后顺序排列的数据称为时间序列。时间序列分为动态时间序列和静态时间序列,时间序列有严格的时间先后顺序。时间序列可以抽象为由一系列二元组组成,记为S={ 由两点组成的序列称为基本的时间序列,如图1所示。 图1 基本序列Fig.1 The basic sequence a:平稳序列,序列值波动很小的序列。 b:上升序列,序列值处于上升趋势的序列。 c:下降序列,序列值处于下降趋势的序列。 时间序列不管怎样复杂多变,都是由这3种基本序列组合而成。 设有两个时间序列S1和S2,度量时间序列的函数sim(S1,S2),当sim(S1,S2)≤ε(ε为指定的阈值,下同),认为时间序列S1和S2满足以ε为界的相似性。 相似函数,sim(S1,S2)同时满足: 正定性:即sim(S1,S2)≥0,当且仅当S1=S2时,sim(S1,S2)=0; 对称性:sim(S1,S2)=sim(S2,S1); 三角不等式:有3个序列S1、S2、S3,有sim(S1,S2)≤sim(S1,S3)+sim(S2,S3)。 时间序列都是由基本序列组合而成,研究时间序列的相似性就自然转化为研究基本序列的相似性。 2.1 平稳序列 平稳序列分为严格的平稳序列和非严格的平稳序列。严格的平稳序列要求序列的值相等,这样的序列在实际应用中并不常见。 定义1:如果序列的方差σ2小于指定的阈值ε,即满足σ2<ε,则称序列为非严格的平稳序列。非严格平稳序列亦称为平稳序列,平稳序列都是相似的。 2.2 上升序列 定义2:序列中的值满足Di-Di-1>ε,称序列为上升序列。 定义3:序列中相邻的值所对应的点相连成为折线,如果折线对应平行,称两序列相似。 如图2所示,A、B两折线互相平行,则称A中的点组成的序列与B中的点组成的序列相似。折线去掉连线仅留节点成为序列,序列相连成为折线,以后序列与折线不加区分。 图2 相似序列Fig.2 Similar sequence 图3 三平行线间线段Fig.3 The line between three parallel lines 证明:由定义和推论易得出结论,略。 2.3 下降序列 定义4:序列中的值满足Di-1-Di>ε,称序列为下降序列。 证明:由定义和推论易得出结论,略。 2.4 序列相似性的局限性 满足定义1、定理1及定理2的时间序列并不多。它要求序列的长度相同,序列的对应比值要小于一个指定的阈值,这样人为因素较多,不利于计算机的自动操作。对于以上的定义及定理必须进行相应的调整,以满足不同序列的相似性比较。 对于任意的两个时间序列A和B,其长度分别为m和n,且m≥n,时间间隔可同或不同。如何判断A和B的相似性,定义如下方法。 定义6:设时间序列A={a1,a2…am}和B={b1,b2,…bn},长度为|A|=m和|B|=n,且m≥n,其比值序列θ={θ1,θ2,…θn-1},θ的均值为μ,均方差为σ。如果θi落在95%的置信区间,即θi∈[μ-1.96σ,μ+1.96σ],由于比值序列均为正值,也可定义为θi∈[0,μ+1.96σ],就称序列B中的bibi+1与序列A相似。 输入:时间序列A={a1,a2…am}和B={b1,b2,…bn} 输出:A和B的相似度sim(A,B)。 步骤 (1)求A和B的长度; (2)计算A和B的比值序列θ; (3)按θ的置信区间计算A与B的相似点集O; 为了检验本文提出的TPSS算法的科学性与合理性,提出了3套方案来对比相似性度量方法的优劣:方案1,用欧式距离计算时间序列的相似性;方案2,利用动态弯曲距离DTW计算时间序列的相似性;方案3,利用TPSS计算时间序列相似性。 实验环境为PentiumIV双核CPU,2GB内存和160GB硬盘,MicrosoftWindowsXP操作系统,开发工具为Java。所用测试数据为2012年某城市两个生活小区每天的用水量,每个小区的记录为366个,共732个数据,如图4所示,上面的是一个小区,下面的是另一个小区。 图4 用水量序列Fig.4 Water consumption series 实验结果表明,与欧式距离相比,TPSS算法剔除了欧式距离的不能垂直移动,两个序列数据要相同及阈值的人为性;与DTW相比,TPSS算法降低了运算量及阈值的人为性。表明TPSS算法能够准确的比较时间序列的相似性。 提出了一种基于两点的时间序列相似性算法TPSS,即利用两个相邻数据组成的基本序列相似性,判断序列的相似性。TPSS算法如下:扫描一次序列数据库,计算比值序列θ及置信区间,进而计算相似度,并确定基本序列是否相似。该算法时间复杂度为O(n)(n为两系列长度较大者),与欧式距离相同,优于DTW。实验结果与理论分析表明,TPSS算法能够实时有效地判断序列的相似性,并给出相似度。 [1] 贾澎涛,何华灿,刘丽,等.时间序列数据挖掘综述[J].计算机应用研究,2007,24(11):15-18. [2] 万定生,张奕韬,余宇峰.基于统计分析的水文时间序列关联规则优化算法[J].微电子学与计算机,2007,24(10):126-129. [3] 郭秀珍,陆建峰,汤九斌.周期性时间序列数据聚类算法的改进研究[J].微电子学与计算机,2011,28(10):118-121. [4] Keogh E,Lin J,Fu A.HOT SAX:Efficiently Finding the Most Unusual Time Series Subsequence[C]//Proc.of the 5th IEEE Int’l Conf.on Data Mining.Newport Beach,USA:IEEE Press,2005:226-233. [5] Keogh E, Chakrabarti K, Pazzani M, et al. Dimensionality reduction for fast similarity search in large time series databases[J].Knowledge and information Systems, 2001,3(3):263-286. [6] 梁建海,张建业.基于斜率偏离的时间序列相似性搜索方法研究[J].计算机应用研究,2010,27(1):54-55. [7] 张雪丽,牛强.基于角点弯曲度的时间序列相似性搜索算法[J].计算机工程,2011,37(15):37-40. [8] 董晓莉,顾成奎,王正欧.基于形态的时间序列相似性度量研究[J].电子与信息学报,2007,29(5):1 228-1 231. [9] 李正欣,张凤鸣,李克武.多元时间序列模式匹配方法研究[J].控制与决策,2011,26(4):565-570. [10] 李海林,郭崇慧.基于多维形态特征表示的时间序列相似性度量[J].系统工程理论与实践,2013,33(4):1 024- 1 034. [11] 朱天,白似雪,王柏,等.基于时间段的时序规则发现[J].通信学报,2009,30(8):112-115. [12] Park S,Kim S W,Chu W W.Segment-based approach for subsequence searches in sequence databases[C]Proceedings of the 16th ACM Symposium on Applied Computing.New York:ACM Press,2001:248-252. [13] 肖辉,胡运发.基于分段时间弯曲距离的时间序列挖掘[J].计算机研究与发展,2005,42(1):72-78. [14] 喻高瞻,彭宏,胡劲松,等.时间序列数据的分段线性表示[J].计算机应用与软件,2008,24(12):17-18. (责任编辑:李华云) Research on the Similarity in Time Series Data with Two Points LIU Yongzhi1,2 1.College of Computer Science and Technology ,Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 210016, China; 2.Department of Information Engineering,Xuancheng Vocational & Technical College, Xuancheng Anhui 242000, China At present, the judgement of the similarity of time series is based on Euclidean distance and DTW(Dynamic Time Warping). These two kinds of methods have some defects. Euclidean distance request the same length of sequence, vertical movement will affect similarity judgment of sequence. Anyone set the threshold of the empirical is difference; DTW is optimized of the Euclidean distance to avoid the consistency of European length. But the other two disadvantages still exist and the computational complexity is increased. This paper proposes a novel similarity algorithm of time series based on the two points, it can calculate any of the two sequence similarity. First, it analyzes the time series form of two points, put forward TPSS method. Secondly, in order to improve the robustness of the similar judgment, reduce the influence of artificial threshold setting, TPSS is developed. Finally, it gives the algorithm and experiment analysis. The experimental results show that tThis algorithm can effectively determine the similarity of arbitrary sequences, improves the robustness and reduces human intervention and can help clustering, prediction in data mining. Time series; Similarity; Data mining; Two points Ratio series 2014-08-27 安徽省质量工程项目(20101452);安徽高校基金重点课题(KJ2014A285) 刘永志(1973-),女,河南杞县人,副教授、高工,博士生,主要研究方向为数据挖掘。 TP391 A 1671-5322(2014)04-0001-04
2 时间序列的相似性



3 时间序列相似性拓展



4 算法

5 性能分析


6 结 语
