基于ITD和切片双谱的滚动轴承局部损伤故障诊断
2014-07-22唐贵基庞彬
唐贵基,庞彬
(华北电力大学 机械工程学院,河北 保定 071003)
滚动轴承局部损伤故障振动信号多为非平稳的多分量调制信号,采用合适的时频分析方法将故障信号分解为若干个单分量AM-FM信号,再对其包络解调是轴承故障诊断的常用手段。本征时间尺度分解(Intrinsic Time-Scale Decomposition,ITD)是文献[1]针对传统时频分析方法的局限性提出的新方法,可自适应性地将一个复杂信号分解为若干个合理旋转(Proper Rotation,PR)分量之和,每个PR分量通过一次迭代即可获得,端点效应小,分解能力强,计算速度明显优于经验模态分解(Empirical Mode Decomposition,EMD)和局部均值分解(Local Mean Decomposition,LMD)方法,有利于实现在线故障诊断[2-3]。
高阶谱分析技术是近年来信号处理的新技术,是分析非Gauss信号的良好工具[4-5]。双谱是高阶谱中运算最简单且应用最广泛的分析方法,在理论上可完全抑制Gauss噪声的影响,识别信号中的二次相位耦合频率成分,提高分析和辨识精度。轴承振动信号中的噪声可近似作为Gauss噪声处理,用双谱分析轴承振动信号更易获得故障特征信息。同时轴承信号常表现为二次相位耦合模式,如轴承故障特征频率自身的耦合及故障特征频率与转频的耦合[6-7]。下文将ITD与切片双谱相结合分析轴承故障振动信号,可有效抑制噪声,提取轴承信号由于二次相位耦合产生的非线性特征,准确进行故障诊断。
1 ITD方法
1.1 原理
设待分解信号Xt的极值为Xk,对应时刻为τk(k=1,2,…,N,N为所有极值点个数)。定义L为基线提取算子,Lt=LXt为信号的基线分量,则Xt被分解为Xt=Lt+Ht,Ht为待提取的PR分量。
(1)L通过相邻基线控制点Lk和Lk+1在[τk,τk+1] (k=1,2,…,N)上对Xt线性变换所得,即[2]
t∈(τk,τk+1),
(1)
其中每个基线控制点为
(1-α)Xk+1,k=1,2,…,M-2,
(2)
式中:α为线性增益,一般取0.5。
(2)定义一个固有旋转分量提取算子LXt,则
(3)
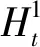
(4)
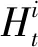
ITD方法中的基线通过信号的线性变换得到,避开了EMD 方法中求极大值和极小值包络时使用的两次、三次样条拟合,从而缩短计算时间,减少拟合误差,所以ITD方法端点效应小且计算速度快。
1.2 新迭代终止条件
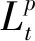

2 切片双谱
零均值平稳随机信号x(n)的三阶累积量d(τ1,τ2)定义为[7]
d(τ1,τ2)=E{x(n)x(n+τ1)x(n+τ2)} ,
(5)
式中:τ1,τ2为时间延迟;E{·} 为统计均值。
双谱B(ω1,ω2)定义为三阶累积量d(τ1,τ2)的二维Fourier变换,即
exp[-j(ω1τ1+ω2τ2)] 。
(6)
由于双谱计算量庞大,当数据长度有限时,双谱估计精度较低。为了减少计算量且提高分析精度,在双谱的基础上发展了切片双谱。
取τ1=τ2=τ,则三阶累积量的对角切片d1D(τ)可定义为
d1D(τ)=d(τ1,τ2)=E{x(n)x(n+τ)x(n+
τ)} 。
(7)
对d1D(τ)进行Fourier变换得到切片双谱为
(8)
3 仿真信号分析
考察的仿真信号为
x(t)=x1(t)+x2(t)+n(t),
(9)
x1(t)=[5+cos(400πt+1)+cos(700πt+2)+cos(1 100πt+3)+cos(1 600πt)]·sin(3 000πt),
x2(t)=[4+cos(30πt+1)+cos(80πt+2)+cos(110πt+3)+cos(400πt+4)]sin(1 200πt),
式中:n(t)为信噪比为-4 dB的Gauss白噪声。采样点数N=20 000,采样频率fs=20 000 Hz。
对x(t)进行ITD,原迭代条件下产生9个PR分量,新迭代终止条件下产生4个PR分量即停止分解。新迭代终止条件下的ITD结果如图1所示。

图1 新迭代终止条件下的ITD结果
PR1和PR2的幅值谱和包络谱如图2所示。x1(t)的载波频率1 500 Hz,x2(t)的载波频率600 Hz分别在PR1和PR2的幅值谱中体现,x1(t)的调制频率200,350,550和800 Hz,x2(t)的调制频率15,40,55和200 Hz分别在PR1和PR2的包络谱中体现,说明ITD方法可将x1(t)和x2(t)从噪声成分中精确分解出来。
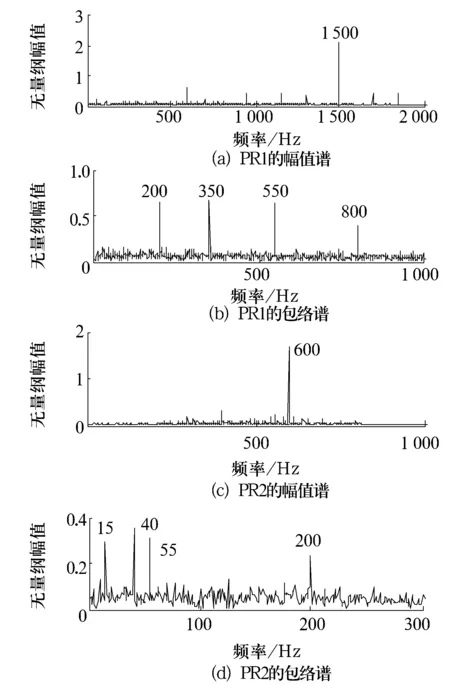
图2 PR1和PR2的幅值谱和包络谱
PR1和PR2的包络切片双谱如图3所示。由图可知,PR1的包络切片双谱与包络谱相比,噪声几乎得到完全抑制,并只在满足二次相位耦合的200,350 和550 Hz频率成分处存在明显谱线,不满足二次相位耦合的800 Hz频率成分被剔除。同理,PR2的满足二次相位耦合的15,40和55 Hz频率成分得到体现,不满足二次相位耦合的200 Hz频率成分被剔除。

图3 PR1和PR2的包络切片双谱
通过仿真分析验证了ITD的能力和切片双谱在抑制噪声与识别二次相位耦合方面的优势。在轴承局部损伤故障振动信号中,故障特征频率满足二次相位耦合关系,而干扰频率通常不满足二次相位耦合关系,将切片双谱应用于轴承故障诊断,有利于抑制噪声和剔除无意义的混叠频率,更易获得轴承故障特征信息。
4 轴承故障诊断实例
结合ITD和切片双谱分别对带有内、外圈局部损伤故障的N205圆柱滚子轴承进行故障特征提取,判断轴承故障类型,并与传统的包络谱方法进行比较,通过分析说明该方法在轴承局部损伤故障特征提取方面的优势。
首先利用电火花分别在内、外圈上加工凹坑来模拟内、外圈局部损伤故障,然后利用试验台测试故障轴承振动信号。试验台如图4所示。加载器给故障轴承施加载荷,轴承零件在负载条件下发生强烈摩擦和碰撞,产生大量噪声成分。通过安装在轴承座上的ICP加速度传感器和NI9234数据采集卡对振动信号进行采集,信号采样频率fs=12 800 Hz,采样点数N=16 384,滚子个数Z=12,滚子组节圆直径Dpw=39 mm,滚子直径Dw=7.5 mm,转轴转频fr=24 Hz,压力角α=0°,通过计算可得内圈故障特征频率fi=171.7 Hz,外圈故障特征频率fe=116.3 Hz。

图4 试验台
内圈故障信号的时域波形和包络谱如图5所示。由于噪声等成分影响,其谱线较乱,不易识别轴承故障特征频率。内圈故障信号的ITD结果如图6所示。内圈故障信号PR1分量的包络谱和包络切片双谱如图7所示。由图7a可知,在24.22,171.9和344.5 Hz处存在峰值,分别对应转频、内圈故障特征频率及其2倍频,可见ITD方法将内圈故障特征信号从原信号中提取出来,但同时存在很多其他无效干扰频率成分,且不能看出内圈故障特征频率和转频的调制特征。由图7b可清晰看到转频及其2倍频、内圈故障特征频率和转频成分的调制特征。基于ITD和切片双谱的轴承故障诊断方法将存在二次相位耦合的转频及内圈故障特征频率成分提取出来,同时剔除无意义的混叠频率,抑制噪声影响,可有效提取内圈故障特征。

图5 内圈故障信号的时域波形和包络谱

图6 内圈故障信号的ITD结果
外圈故障信号的时域波形和包络谱如图8所示。原信号由于噪声等干扰成分存在,不易提取外圈故障特征信息。外圈故障信号的ITD结果如图9所示。外圈故障信号PR1分量的包络谱和包络切片双谱如图10所示。PR1分量的包络谱在116.4 Hz处存在明显谱线,对应外圈故障特征频率,但其倍频成分淹没在噪声中,不易识别。PR1分量的包络切片双谱峰值频率对应外圈故障特征频率116.4 Hz及其2倍频232.8 Hz,外圈故障特征更直观。

图8 外圈故障信号的时域波形和包络谱

图9 外圈故障信号的ITD结果
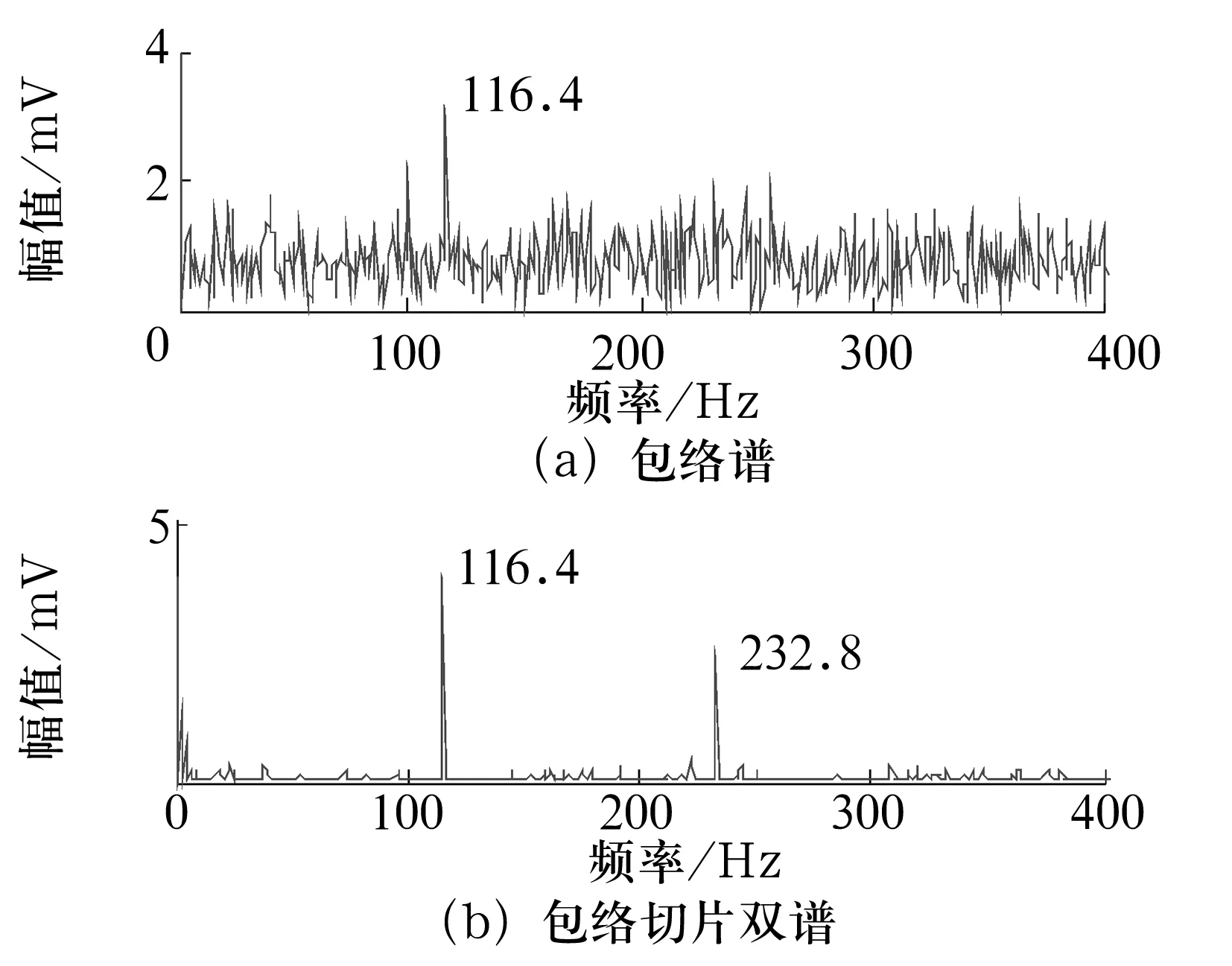
图10 外圈故障信号PR1分量的包络谱和包络切片双谱
轴承实际局部损伤故障振动信号中往往混杂噪声和其他干扰频率成分,传统的故障诊断方法不易提取故障特征。基于ITD和切片双谱的轴承局部损伤故障诊断方法可有效抑制噪声,同时剔除无意义的混叠成分,为轴承局部损伤故障诊断提供一种新途径。
5 结束语
ITD方法作为一种时频分析新方法,对信噪比较差的信号具有很好的分解效果,通过改进其迭代终止条件,进一步加快了ITD方法的分解速率,将其应用于轴承局部损伤故障诊断,可很好地从原始振动信号中提取轴承故障特征信号分量,与切片双谱结合分析可进一步抑制噪声,识别轴承局部损伤故障信号中的二次相位耦合现象,判断轴承故障类型。通过轴承内、外圈故障诊断实例验证了该方法的有效性。
