基于Kalman滤波和谱峭度的滚动轴承故障诊断

刘志川，唐力伟，曹立军

(军械工程学院 火炮工程系，石家庄 050003)

滚动轴承广泛应用于旋转机械中，是常见的易损件。轴承故障会导致机器出现振动和噪声，严重时会影响整台设备的正常运行，因此轴承的状态检测和故障诊断具有重要意义。

共振解调技术是目前轴承故障诊断中普遍使用的方法，但是存在带通滤波器参数难以确定的问题，传统的小波和小波包分析技术均不能自适应选择最优带通，导致应用受限。谱峭度[1]的基本原理是通过计算频域中每根谱线的峭度值，从而在频域中定位瞬态冲击。文献[2]提出将谱峭度值作为短时Fourier窗口函数，通过谱峭度图选择带通滤波器的参数。针对谱峭度图计算耗时的问题，文献[3]提出了快速谱峭度图的概念。文献[4]则指出在信噪比较高的情况下，谱峭度能够较好地识别瞬态冲击信号。轴承工作环境相对复杂，环境噪声较大，而复杂工况对谱峭度计算值会产生影响，从而给最优带通滤波的带宽和中心频率的计算带来误差，影响诊断效果，因此有必要对信号进行降噪预处理。

Kalman滤波是一种动态数据处理方法，属于递推式滤波方法[5]，可以克服传统时频分析方法不适用于处理非平稳信号的问题，对测量数据逐一处理，由递推方程随时给出某一时刻新的状态估计值，并与该时刻后的数据一起做出下一状态的最优估计，达到信号降噪目的。在此，针对轴承内、外圈裂纹故障，将Kalman滤波与快速谱峭度图相结合，以实现轴承的故障诊断。

1 AR模型

1.1 参数估计

对于时间序列{xt}，t=1，2，…,N，AR模型为

xt=φ1xt-1+φ2xt-2+…+φnxt-n+at，

(1)

式中：φ2,…，φn及σa是AR模型[6]的参数;n为模型阶次。参数估计即估计出这n+1个数值，由于

at=xt-φ1xt-1-φ2xt-2-…-φnxt-n，

(2)

(3)

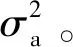
1.2 模型阶数

AR模型的阶次n未知，需要在递推过程中确定。在递推过程中，可以给出低阶到高阶的每一组参数，模型的最小预测误差功率P是递减的，当Pn达到最小值或者不再变化时，此时的阶次就是AR模型的正确阶次。

定阶是建立AR模型的关键过程，其中AIC准则(Akaike Information Criterion)应用较为广泛。它由2项构成：第1项随阶数增大而变小，体现模型拟合好坏；第2项随阶数增大而变大，体现模型参数多少。AIC准则表示为

AIC(n)=Nln(Pn)+2n。

(4)

从n=0开始增加模型阶数，AIC(n)先减小,后增大。当阶数n达到某一值n0时，AIC(n0)最小，则n0即为AR模型的最合适阶次。

2 Kalman滤波

Kalman滤波是工程应用较为成熟的一种递推线性最小方差估计，能够通过前一时刻的最优值与当前时刻的测量值一起给出当前时刻的最优估计，能够对测量数据进行实时更新。通过对原始数据建立的AR模型可以构建Kalman滤波的5个基本方程。

设齿轮箱振动真实信号为x(t),t=1,2,3,…，N，观测噪声为R，观测值为y(t)，则观测方程可表示为

y(t)=Hx(t)+R,

(5)

其中H=[1 0 … 0]1×n。设系统状态为s(t)=[x(t),x(t-1),…,x(t-n+1)]T，则状态转移方程可表示为

s(t)=As(t-1)+a(t)，

(6)

其中In-1为n-1维单位阵。由此可建立Kalman滤波的5个基本方程：

(1)假设系统现在状态为t，根据上一时刻状态预测现在的状态为

s(t|t-1)=As(t-1|t-1)+a(t);

(7)

(2)s(t|t-1)时刻协方差更新为

P(t|t-1)=AP(t-1|t-1)A′+Q;

(8)

(3)更新Kalman增益为

K(t)=P(t|t-1)H′/[HP(t|t-1)H′+R];

(9)

(4)新观测得到的状态最优估计值为

s(t|t)=X(t|t-1)+K(t)[y(t)-

Hs(t|t-1)];

(10)

(5)s(t|t)时刻协方差更新为

P(t|t)=[I-K(t)H]P(t|t-1),

(11)

式中：P为协方差；Q为系统过程噪声；R为测量噪声；K(t)为系统增益；I为单位矩阵。

3 谱峭度

信号的Wold-Cramer分解在频域的表达式为

(12)

式中：H(t,f)为t时刻冲击响应h(t,f)的频域表示，是一个复包络函数。

定义Y(t)过程的4阶谱累积量为

(13)

2n阶的谱瞬时矩为

S2nY(f)E{|H(t,f)dX(f)|2n}/df。

(14)

则谱峭度定义为

谱峭度[7-8]是关于中心频率和带宽的函数，当带宽无限小时，谱峭度为0，当带宽过大时，谱峭度无法反映频带范围中的瞬态冲击现象。快速谱峭度图的原理是找到一个中心频率fs和带宽Bw，使峭度达到最大值，这时对应的中心频率和带宽即最优滤波器的2个参数。快速谱度图是平面上的二维图，图中颜色的深浅代表不同中心频率和带宽组合下的峭度值，颜色最深处峭度值最大，对应获得最优滤波器的中心频率和带宽。

4 基于Kalman滤波和谱峭度的故障诊断方法

轴承工作环境常常有较大噪声，为降低振动信号噪声，提高故障特征，先采用Kalman滤波技术对振动信号进行降噪预处理，然后利用快速谱峭度图确定最优滤波器的中心频率和带宽。应用能量算子解调法解决传统Hilbert包络解调过程中存在的信号两端调制和计算量大的问题，然后对包络进行FFT变换得到包络谱，将包络谱中峰值较大的频率成分与轴承故障特征频率相比较，实现诊断，其流程如图1所示。

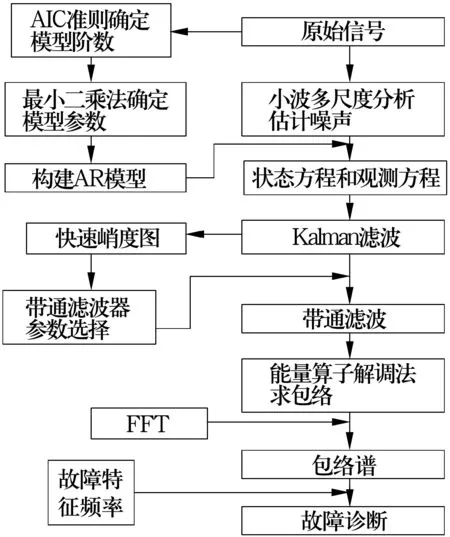
图1 轴承故障诊断方法流程图

5 试验验证

轴承内、外圈故障实测信号来自二级减速器试验平台，试验轴承为6206型深沟球轴承，钢球个数Z=9，钢球直径Dw=9.5 mm，球组节圆直径Dpw=46.5 mm。采用线切割分别在轴承的内圈和外圈上加工宽度0.5 mm、深度1 mm的细小裂纹作为故障。采集信号时，振动加速度传感器B&K4508固定在故障轴承所在的轴承座上，采样频率为10 kHz；转速由JN338型转速转矩传感器测量。

5.1 内圈故障

输入轴转速为610.20 r/min，故障频率f=27.55 Hz，中间轴转动频率fr=5.08 Hz，采样时间为2.5 s。

首先通过原始信号建立系统AR模型，利用AIC准则计算得到的AIC曲线如图2所示，从曲线中可以看出，阶数取50时，AIC有极小值，因此确定模型阶数为50。

图2 AR模型的AIC曲线

Kalman滤波过程中，过程噪声和观测噪声是2个重要参数[9]。观测噪声使用小波变换降噪的方法提取，对振动信号进行小波多尺度分解，得到小波系数，设置合适的阈值，大于阈值的小波系数置零，对保留的小波系数进行逆变换即为噪声信号。过程噪声在滤波过程中由大量试验数据确定。轴承内圈故障信号滤波前、后的时域图如图3所示，从图中可以明显看出，滤波后信号幅值减小，冲击更加明显。

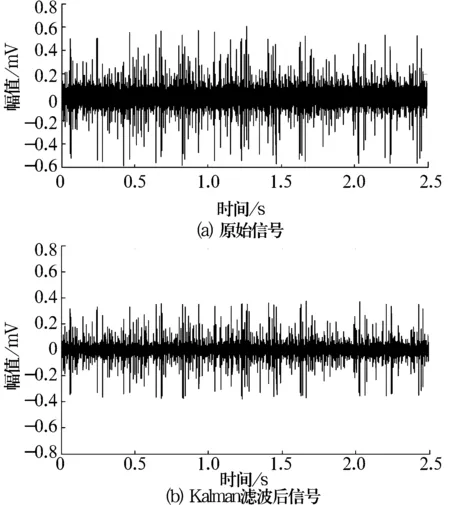
图3 轴承内圈故障信号滤波前、后时域图

对滤波后的信号进行谱峭度计算，绘制快速谱峭度图，如图4所示。

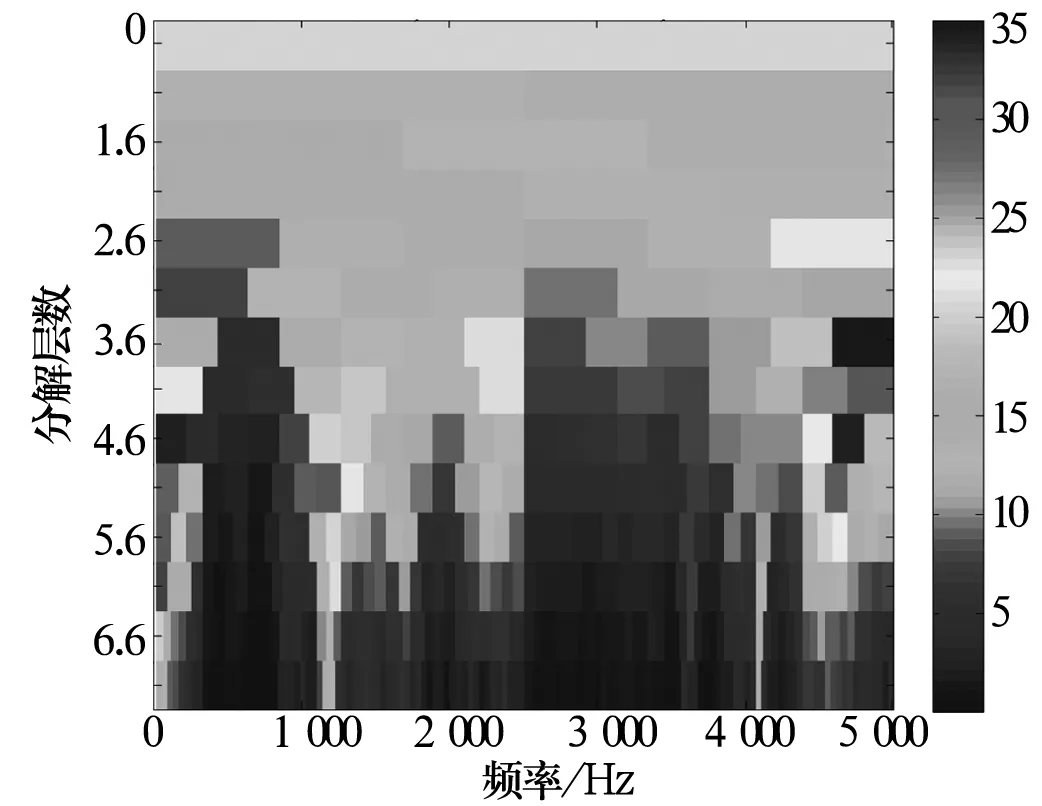
图4 滤波后内圈故障信号的快速谱峭度图

由图4可知，在中心频率为4 791.67 Hz、带宽为416.67 Hz的频带内，峭度达到最大值35(在3.6层内)，其他频带信噪比较低。以此中心频率和带宽为带通滤波器的最优参数对信号进行带通滤波，并对带通滤波后信号进行能量算子包络解调，结果如图5所示。图中可以看出与内圈裂纹故障特征频率接近的27.48 Hz及其倍频等，而且故障轴承所在轴的转动频率(5.09 Hz)非常明显，从结果可以判断是内圈故障。

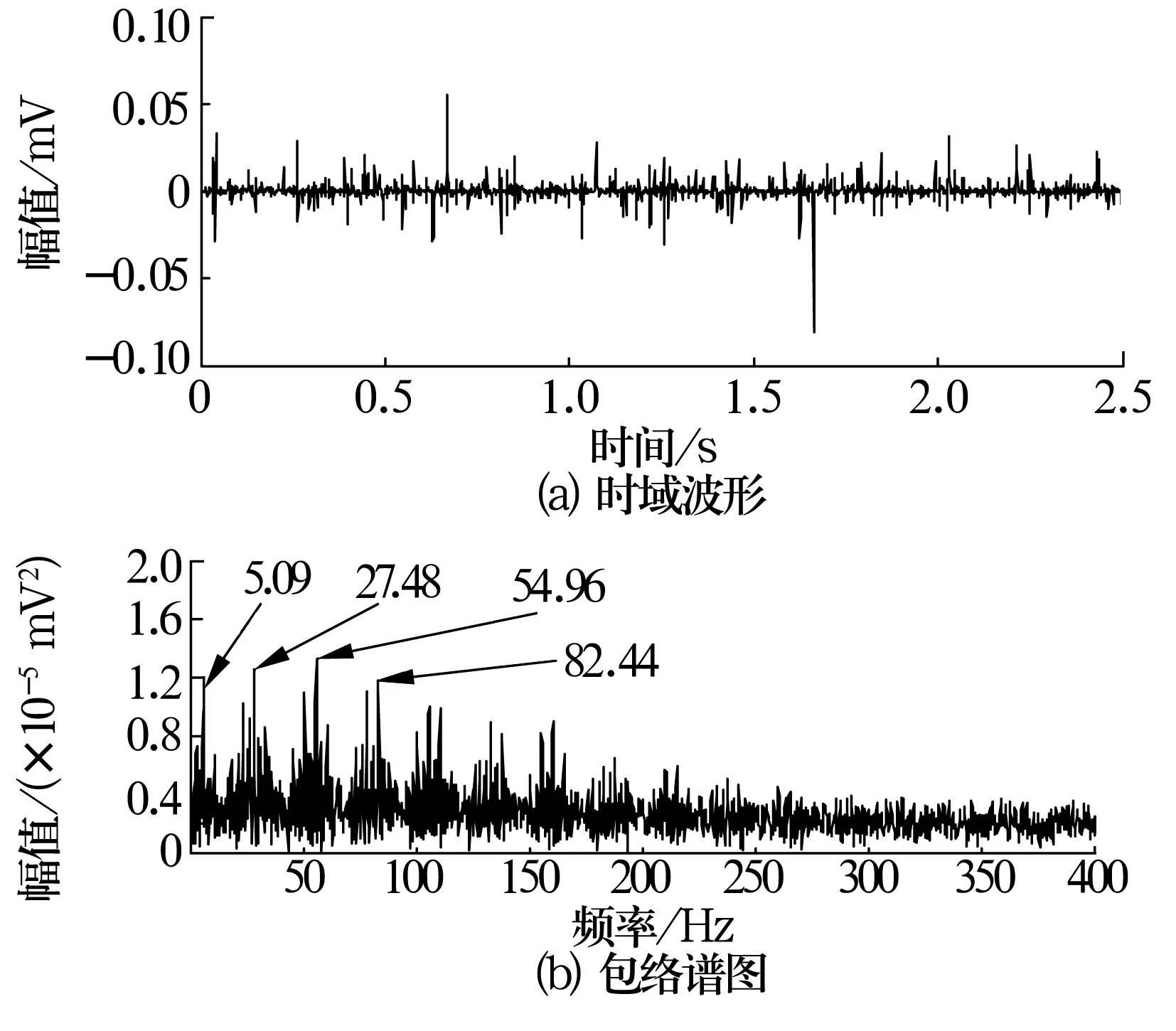
图5 带通滤波后内圈故障信号时频图

5.2 外圈故障

输入轴转速为1 488.5 r/min，故障频率f=44.41 Hz，中间轴转动频率fr=12.4 Hz，采样时间为1 s。对采集到的信号进行Kalman滤波及谱峭度计算，绘制的快速谱峭度图如图6所示。由图可知，在中心频率为4 375 Hz、带宽为1 250 Hz的频带内峭度达到最大值13.6(在2层内)。对信号进行带通滤波和能量算子包络解调，结果如图7所示，可以看出与外圈裂纹故障特征频率接近的44.26 Hz及其倍频等，而且故障轴承所在轴的转动频率(12.52 Hz)非常明显，从结果可以判断是外圈故障。

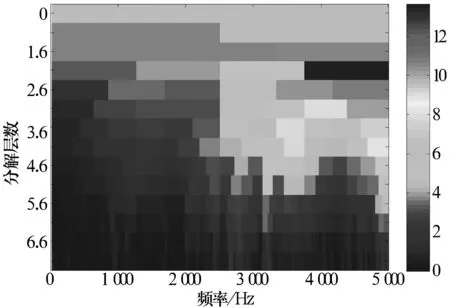
图6 滤波后外圈故障信号的快速谱峭度图

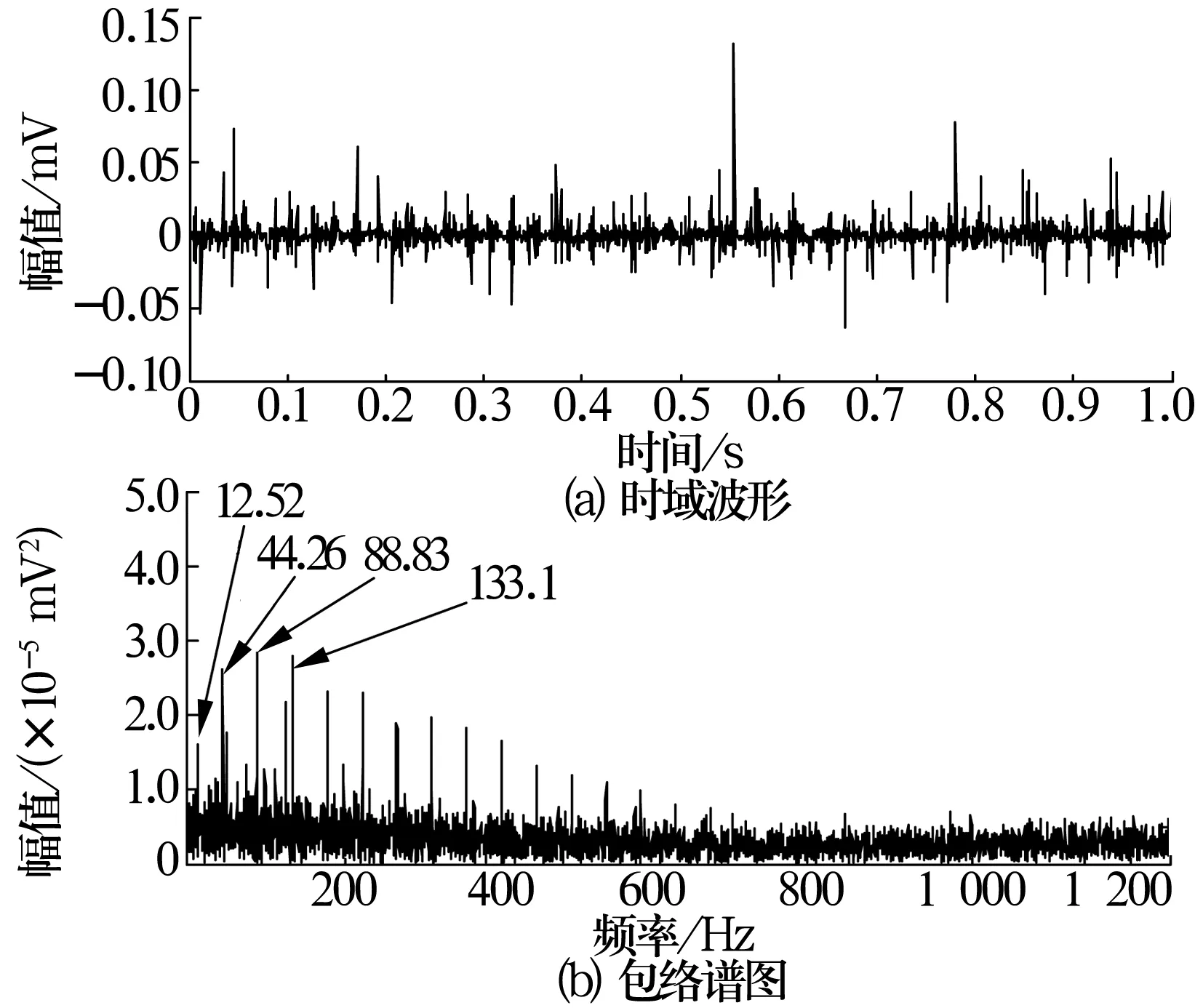
图7 带通滤波后外圈故障信号时频图

6 结束语

为解决传统包络分析方法中心频率和带宽参数难以确定的问题，提出了基于Kalman滤波和谱峭度图的轴承故障诊断方法。首先建立系统AR模型，对原始信号进行Kalman滤波降噪预处理，提高信噪比，然后利用谱峭度自适应确定最优滤波器的中心频率和带宽，最后利用能量算子解调法对带通滤波后的信号进行包络解调分析，结合轴承故障特征频率实现故障诊断。

对工程信号的分析处理验证了本方法的可行性，而且在转速相对较低的情况下也可以成功诊断出轴承内、外圈故障，为低速无载荷轴承故障诊断提供了新的研究方向。