基于全矢局部均值分解的滚动轴承故障诊断方法

2014-07-21苏文芳李凌均韩捷石帅锋

轴承 2014年11期

苏文芳，李凌均，韩捷，石帅锋

(郑州大学振动工程研究所，郑州 450001)

滚动轴承是应用广泛、易损伤的机械零部件，其状态监测和故障诊断非常重要[1]。由于受载荷、摩擦力、阻尼、传播路径和噪声等多种因素的影响，实际采集到的包含轴承故障信息的振动信号大多是多分量的调幅调频信号。

由局部均值分解(Local Mean Decomposition，LMD)方法得到的每个PF分量(Product Function)，实际上是一个单分量的调幅调频信号, 因此LMD方法本质上是将多分量信号自适应地分解为若干个单分量的调幅调频信号之和, 非常适合于处理多分量的调幅调频信号[2-5]。

由于单通道信号不能全面反应系统的非线性特征，存在信息遗漏的问题，甚至由同一截面2个单通道信号分析得出的结论也往往不一致，故需要对获取的信号进行信息融合。全矢谱技术可以有效融合同一个截面的双通道信息，真实地反应信号特征。

根据全矢谱的兼容性，将其与LMD相结合，提出了一种新的信号处理方法——全矢局部均值分解(FVLMD)方法，并通过滚动轴承故障信号验证了其可行性。

1 局部均值分解

LMD是一个逐渐去除信号高频成分的过程。对于任意信号x(t), 首先找出所有的局部极值点ni, 然后求取相邻2个极值点ni和ni+1的平均值mi,得到局部均值函数m11(t)。并用极值点ni求包络估计值ai，得到包络估计函数a11(t)。

将局部均值函数m11(t)从原始信号x(t)中分离出来, 得

h11(t)=x(t)-m11(t)。

(1)

用h11(t)除以包络估计函数a11(t),对h11(t)进行解调, 得

s11(t)=h11(t)/a11(t)。

(2)

经迭代变换得到包络信号a1(t)和纯调频信号s1n(t)，将这2个信号相乘便得到第1个PF分量

基于改进型非线性函数的NLSEF是TD和ESO变量之间的非线性误差控制率，与ESO对总扰动的补偿值一起组成控制量。传统的NLSEF只是用到误差信号的比例和微分进行非线性计算，而改进型NLSEF加上了信号的积分环节，提高了系统的控制精度，增强了系统的抗扰性以及鲁棒性。它算法表达式如下：

PF1(t)=a1(t)s1n(t)。

从原始信号x(t)中将第1个PF分量PF1(t)分离出来, 得到一个新的信号u1(t), 将u1(t)作为原始数据重复以上步骤, 循环k次, 直到uk为一个单调函数为止。

(3)

至此, 将原始信号x(t)分解为k个PF分量和1个单调函数uk之和, 即

(4)

完整原始信号x(t)的时频分布即为所有PF分量的瞬时幅值和瞬时频率的组合。

2 全矢谱分析方法

由单一通道信号分析得到的旋转机械信号特征往往不全面，带有较大的片面性，需要同时考虑相互垂直2个通道所反映的信息。

假定x，y方向上的离散序列分别为{xn}和{yn}，n=0,1,2,…,N-1。对其进行Fourier变换得到{Xk}和{Yk}，k=0,1,2,…,N-1。构建复序列{zn}为

{zn}={xn}+j{yn}。

(5)

对(5)式进行Fourier变换得{Zk}，且

(6)

(7)

式中：RLk为主振矢；RSk为副振矢。

全矢谱在算法上大大减少了计算量，且结构较稳定，对于单通道信号同样适用，完全可以满足实时监测分析要求[6]。

3 全矢局部均值分解

LMD主要进行复杂信号的筛分，为了实现同源多通道信息的处理，根据全矢谱的兼容性[7]，将其与LMD相结合，形成一种新的信号处理方法——全矢局部均值分解。其计算过程如下：

(1)将同源双通道信号x1(t)，x2(t)分别进行LMD处理，得到各自的PF分量。

(2)将对应的PFi1(t)和PFi2(t)(i=1，2，…，n)作为全矢谱同源信息进行融合。其流程图如图1所示。

图1 全矢局部均值分解流程图

4 试验分析

试验在Spectra Quest公司研制的风力涡轮机动力传动系统诊断模拟器上进行，试验装置如图2所示。

图2 轴承故障试验台

采用输出轴端存在内圈故障的轴承，在轴承座水平和垂直方向分别安装电涡流传感器采集振动信号。电动机转速为1 800 r/min，即旋转频率为f=30 Hz，采样频率为8 192 Hz。轴承型号为6002-2RS，钢球数Z=9。根据轴承故障特征频率公式计算各部位故障频率，结果见表1。

表1 轴承各部位故障特征频率 Hz

对2个互相垂直方向的信号进行LMD处理，时域图及LMD结果如图3和图4所示。

图3 水平信号时域图及LMD处理结果

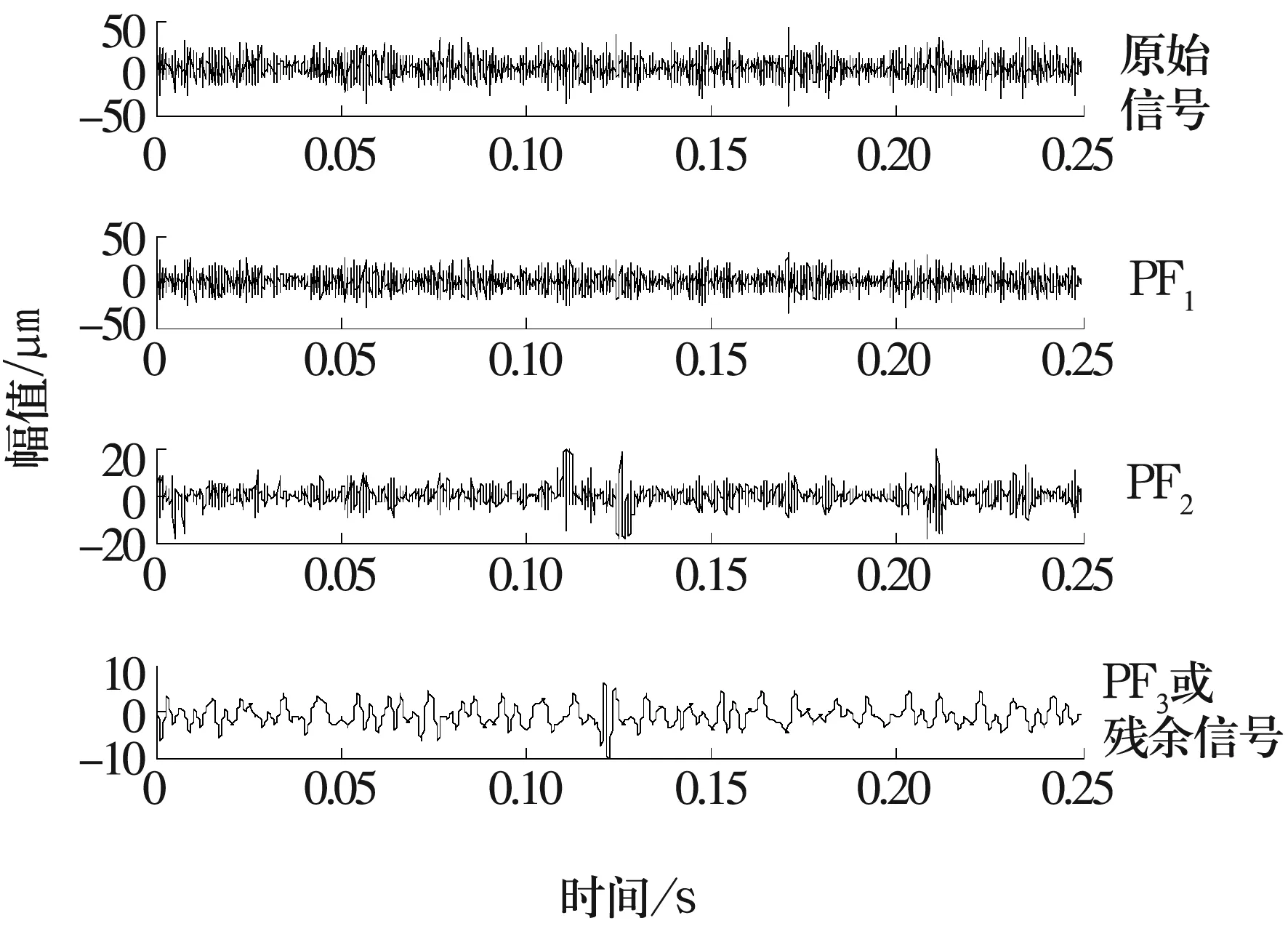
图4 垂直信号时域图及LMD处理结果

对比图3与图4可知，水平方向信号和垂直方向信号存在一定的不同，其LMD处理结果也存在差异。对2个信号的相应PF分量进行频谱变换，结果如图5和图6所示。由图可以看出，2个同源信号对应PF频谱图的频谱结构和能量分布呈现出不同的特征。

对比图5和图6可以看出，图5中PF1分量的频谱在160 Hz(接近内圈故障特征频率)及其2～4倍频处有明显幅值，且能量依次减弱；图6中PF1频谱在这些频率处也有明显幅值，只是能量不是依次减弱。同时由于转频的调制作用，图5和图6中的PF1频谱在160 Hz周围都存在较明显的边频带，另外在图5的PF1中还出现了转频的2倍频，在图5和图6的PF2中也出现了32 Hz(约等于转频)的幅值特征，由此可以判断轴承内圈出现了故障。

图5 水平信号PF1,PF2的频谱图

图6 垂直信号PF1,PF2的频谱图

除此之外，在图5的PF1频谱中有108 Hz(接近于外圈故障频率)的幅值存在，而图6的PF1频谱中则没有该频率，不能断定外圈是否存在故障。因此对2个信号所分离出来的对应PF作为同源信息进行全矢谱融合，结果如图7和图8所示。

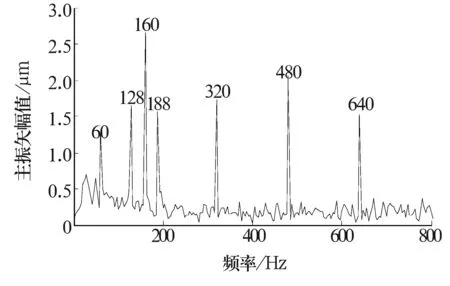
图7 融合后的PF1分量

图8 融合后的PF2分量

从图7可以看出，融合后的PF1分量频谱图更加全面准确。它包含了内圈故障频率特征及其调制频率特征，还包含转频倍频特征，很好地融合了2个相互垂直方向信号的差异性；图8融合后的PF2频谱图中存在32 Hz的峰值，可以判定轴承存在内圈故障。由于在图7中融合后的PF1频谱中未出现108 Hz特征，故判断不存在外圈故障，与实际情况一致，说明全矢局部均值分解方法有效可行。