实体保持架调心滚子轴承主参数优化思路
2014-07-21陈龙李中林郑昊天夏新涛邱明
陈龙,李中林,郑昊天,夏新涛,邱明
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.洛阳成邦轴承有限公司,河南 洛阳 471003)
1 概述
调心滚子轴承径向承载能力高、调心性能良好、能补偿同轴度误差,特别适合在重载或冲击载荷下工作,因而得到广泛应用[1]。
调心滚子轴承保持架分为冲压窗式保持架、黄铜保持架、钢制车削保持架以及塑料保持架。保持架结构形式决定了制造保持架的材料、轴承的引导方式和轴承内部空间大小。考虑轴承内部容许滚动体的安装空间,采用冲压保持架与塑料保持架的调心滚子轴承内部空间相对较大,而实体保持架(主要包括黄铜保持架和钢制车削保持架)内部空间相对较小。
钢制保持架成本低,但其重量大、自润滑性能差、塑变能力差,因而同样结构的轴承,黄铜保持架使用效果相对好。采用黄铜作为原材料时,由于离心浇铸、机加工成形的过程中会产生大量的有害气体及金属碎屑,对周边的环境破坏较大,因此,在条件允许的情况下,可采用较环保的冲压窗式结构设计[1-4]。
冲压窗式保持架采用优质碳素结构钢,其抗拉强度得到较大提高;通过增加滚子数量(或增加滚子直径与长度),提高了轴承的径向承载能力;具有较高的极限转速和较低的摩擦损耗,使其使用寿命得以提高[5-7]。
冲压窗式保持架的发展主要受限于冲压工艺条件,尺寸过大的冲压保持架的加工精度难以保证,而且其引导效果较差,因此,实体保持架仍然大量应用于调心滚子轴承。
文中以采用实体保持架的调心滚子轴承为研究对象,分析其主参数优化过程及约束条件,通过对比国内外3家公司生产轴承的参数,给出优化约束条件的建议。
2 主参数优化
调心滚子轴承多在低速重载下工作,其失效形式主要是零件接触表面的疲劳破坏,因此,将轴承的疲劳寿命作为设计的目标函数。滚动轴承疲劳寿命计算公式为[8-13]
(1)
式中:L10为滚子轴承的基本额定寿命;Cr为轴承的基本额定动载荷;P为轴承的当量动载荷。
由(1)式可以看出,当使用条件一定时,轴承的基本额定动载荷越大,轴承的疲劳寿命越长。
2.1 优化过程[8-10]
调心滚子轴承的额定动载荷为
(2)
额定静载荷为
(3)
式中:bm为材料系数;fc为与轴承零件几何形状、制造精度及材料有关的系数;Lwe为滚子的有效长度;Dwe为滚子的有效直径;Dpw为滚子组节圆直径;Z为滚子个数;i为滚子列数,i=2;α为接触角[8-13]。
由(2)式和(3)式可知,调心滚子轴承的额定动、静载荷主要与滚子的有效直径Dwe、有效长度Lwe、滚子个数Z和接触角α有关,因而可建立优化目标函数
(4)
将其中的4个变量Dwe,Lwe,Z,α分别作为主参数x(1),x(2),x(3),x(4),则
X=[x(1),x(2),x(3),x(4)]T=
[Dwe,Lwe,Z,α]T。
(5)
2.2 约束条件
调心滚子轴承优化设计约束条件主要包括滚子直径Dwe、滚子长度Lwe、外圈最小壁厚he、滚子个数Z、内外圈壁厚差、接触椭圆长轴以及滚子到端面的距离等。为了使额定动载荷Cr尽可能大,主参数的优化过程需满足以下约束条件
ADwe1(D-d)≤Dwe≤ADwe2(D-d),
(6)
ALwe1B≤Lwe≤ALwe2B,
(7)
Ahe1(D-d)≤he≤Ahe2(D-d),
(8)
(9)
(10)
式中:ADwe1,ADwe2,ALwe1,ALwe2,Ahe1,Ahe2,AZ1,AZ2为取值系数;Bk为宽度取值系数,其取值范围参见文献[10];E为外圈滚道直径;D为轴承外径;d为轴承内径;B为轴承宽度。
2.3 优化方法
滚动轴承优化设计过程中,目标函数是优化设计变量的高阶函数,其约束条件较多且为非线性的参数不等约束,因而滚动轴承优化设计属于有约束优化。常用的有约束优化方法包括二次插值法、网格法、增广拉格朗日算法、惩罚函数法、共轭梯度法、遗传算法、复合形法及函数双下降法等[14-17]。
滚动轴承优化设计方法一般采用网格法、惩罚函数法、综合约束函数双下降法、遗传算法等方法。对于滚子轴承,不同的制造工艺对其尺寸系列化的影响不大,而优化后的主参数差异较大。文中以综合约束函数双下降法为例介绍内引导、浮动中挡圈、CA型保持架调心滚子轴承的主参数优化过程[14]。
考虑调心滚子轴承主参数优化中主参数个数,综合约束函数双下降(SCDD)法求解f(x)的一组解向量为
x={x1,x2,x3,x4},
且f(x)max=1/f(x)min,则所求函数解为f(x)的极小值。函数的可行域为
G={x|x∈En,gi(x)≥0,
i=1,2,3,…,9)}。
(11)
引进所有约束函数组成综合约束函数,即
(12)
若
gi(x)≥0,i=1,2,3,…,9,
(13)
则有
S(x)≡0,
(14)
反之亦然。故函数的可行域又可表示为
G={x|x∈En,S(x)=0}。
(15)
依此进行如下迭代,迭代收敛准则为ε1,ε2。
首先选定初始点x(0)和初始步长t0及非负实数参数α0,β,γ,δ,λ,μ,令
S0=α0t0,
(16)
得到初始近似可行域为
G0={x|x∈En,S(x)≤S0}。
(17)
从给定的初始点x(0)出发,对目标函数f(x)按负梯度方向以步长t0进行下降迭代。若所得到的新点落在可行域G0内,则从该点出发,再对f(x)进行下降迭代;否则,从该点出发,对综合约束函数S(x)按负梯度方向以步长τ0=α0t0进行下降迭代。
一般地,当某一新点x(k)属于第k次可行域,
Gk={x|x∈En,S(x)≤Sk},
(18)
则从x(k)出发,对f(x)按负梯度方向以步长tk进行下降迭代,并要求新的点x(k+1)落在Gk;若x(k+1)不在Gk,则从x(k+1)出发,对综合约束函数S(x)按负梯度方向以步长τk=βtk进行下降迭代,直至得到属于Gk的点,并以此作为G(k+1)点,这时,根据相对收敛准则
(19)
若满足(19)式,说明已得到预期的收敛结果;否则,需进一步校验f(x(k+1))和f(x(k))关系。
若
f(x(k+1))≥f(x(k)),
(20)
则缩短步长,令
tk+1=γtk(γ<1)。
(21)
若
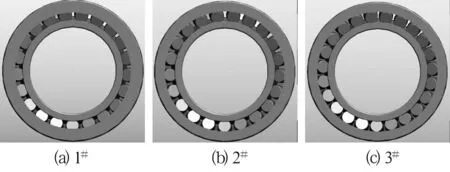
f(x(k+1)) (22) 且 ‖x(k+1)-x(k)‖≥tk, (23) 则取 tk+1=δtk(δ<1), (24) 否则取 (25) 令 Sk+1=α0tk+1, (26) 返回进行下一次迭代。 通过以上循环迭代过程可得一组解向量为x={x1,x2,x3,x4},即{Dwe,Lwe,Z,α}。 主参数优化过程中得到的一组主参数值间接确定了轴承内部其他零件的几何尺寸,为保证装配,需进行约束验算。 滚子直径Dwe系数检验式为 (27) (28) 式中:ADwemax为滚子直径系数最大值;ADwemin为滚子直径系数最小值。 滚子长度Lwe系数校验式为 (29) (30) 式中:ALwemax为滚子长度系数最大值;ALwemin为滚子长度系数最小值。 外圈最小壁厚he系数校验式为 (31) (32) 式中:Ahemax为外圈最小壁厚系数最大值;Ahemin为外圈最小壁厚系数最小值。 轴承装配后滚子端面不能凸出套圈端面,需校验轴承装配后滚子端面至套圈端面的距离 Lrr=0.5(B-Esinα-Lwecosα)- 0.02B≥0。 (33) 内引导时,内圈挡圈位置外径与中隔圈之间引导间隙大于给定值,即 d3-Di1-r≥0, (34) 式中:d3为中挡边圈引导面直径;Di1为内圈中挡边平台直径;r为引导间隙量(一般d3>250 mm时,引导间隙为1 mm;否则为0.5 mm)。 内圈中挡圈引导面宽度应大于中挡圈内径面宽度,即 2ξ-bf≥0, (35) 式中:2ξ为内圈中挡圈引导面宽度,要求大于3 mm;bf为中挡圈内径面宽度。 保持架最小梁宽校验式为 (36) 式中:2YW为保持架兜孔中心线与端面交点直径;Dp为保持架兜孔直径。 对于整体式保持架,要求保持架外径小于外圈端面与端面相交倒角后直径,即 D2-Dc≥0, (37) Dc=dc+0.78Dwe, (38) 式中:Dc为保持架外径;D2为外圈端面与端面相交倒角后直径;dc为保持架内径。 由调心滚子轴承的几何结构可知,最小壁厚he直接决定了外滚道曲率,外滚道曲率与滚子直径及滚子长度共同决定调心角,而滚子长度与调心角决定了内圈中挡圈位置的宽度以及中挡圈内径宽度,中挡圈外径确定保持架内径,保持架的外径由保持架内径和滚子决定,其大小决定装配是否能够完成。由此可知,采用实体保持架的调心滚子轴承主参数优化中直接参数为最小壁厚he与保持架外径Dc。已知3个公司的24196轴承参数对比见表1,表中,1#为国产轴承,2#和3#为国外公司的轴承;fe和fi分别为外圈、内圈沟曲率半径系数。 依据表1中的参数绘制3个公司生产的24196轴承模型如图1所示。 表1 不同公司生产的24196轴承结构参数对比 图1 不同公司生产的24196轴承模型 由表1可知,1#与2#轴承的滚子个数相同,但2#轴承的滚子直径与滚子长度均大于1#。1#轴承滚子直径与个数的乘积(Dwe×Z)为3 255 mm,2#轴承中该乘积为57 309 mm,二者圆周方向占用空间(Dwe×Lwe×Z)之差为168 mm2;由于轴承内、外径的限制,滚子直径加大将相对减小内、外圈壁厚,对于主参数的直接影响是最小壁厚减小。对比1#和2#轴承最小壁厚he之差与滚子直径Dwe之差可知,滚子直径的增加完全偏向于外滚道方向,该设计能较好保证内圈壁厚和轴承寿命。同时,滚子组节圆直径的增加,保证了圆周方向空间尺寸以适应滚子尺寸的增加并且满足保持架强度要求。由于轴承宽度以及中隔圈几何尺寸的限制,必须增大调心角才能使滚子长度增加,因而2#轴承调心角大于1#轴承。但增大调心角,还需要外滚道球面半径的支撑方向有足够的空间以满足几何布局要求,这也是滚子直径加大量偏向外滚道的另一原因。另外,调心角的增加加大了调心滚子轴承的轴向承载能力。对比图1a与图1b可知,由于外滚道曲率不同,图1a外圈端面宽度明显大于图1b,虽然2#轴承的滚子直径比1#轴承的大4 mm,但二者滚子个数相同,滚子之间间隔距离相差不大,可保证保持架梁宽。对比1#和2#轴承的主参数可知,1#轴承的主参数设计保守,额定载荷的差异也非常明显。表1中的额定动、静载荷为样本标注数据,将测绘的主参数代入(2)式计算,则2#轴承计算出的额定动载荷为1#轴承的1.13倍,表1中的数据大于计算值的原因在于国外轴承的额定载荷计算中选取了较高的材料系数以及与轴承零件几何形状、制造精度相关的系数。 对比2#与3#轴承可知,滚子直径相差2 mm,但3#轴承滚子个数多,其圆周方向占用的空间为468 096 mm2,比2#轴承大29 952 mm2,比1#轴承大87 261 mm2。而3#轴承的外滚道直径E仅为737.4 mm,虽远大于1#轴承,但仍小于2#轴承。对比图1b与图1c可知,3#轴承的滚子间隔较小,由于滚子个数与直径乘积大,其设计方案的额定载荷也显著高于其他方案。 依据3#轴承的外滚道直径以及外滚道非装配倒角尺寸(由于滚子长度限制,倒角尺寸不能过大),计算外圈端面与端面相交倒角后直径D2=695.87 mm。根据3#轴承的主参数进行计算得到保持架外径Dc=714 mm,测绘实物外径尺寸为716 mm,二者都远大于外圈端面与端面相交倒角后直径D2,这与约束检验条件(37)式矛盾,无法实现装配。 3#轴承中所使用的保持架结构如图2所示,其采用了剖分式结构,用螺栓连接,连接孔如图2a所示。整个保持架主体剖分为4部分(图2b),每部分呈180°半圆,2片对接后形成一个360°整圆,对接位置由定位台阶定位,保证连接精度;2件对接的360°保持架接口位置互相垂直,组成一个完整的CA型保持架。在装配过程中,便于将180°实体放入内外圈之间,利用外滚道凹入的空间位置对接360°实体完成装配,如图2c所示。 图2 3#轴承的保持架结构 对3#轴承保持架进一步测绘发现其兜孔形状与1#和2#轴承轴承均不同。1#,2#轴承为两段直线弧相交结构,3#轴承则采用球形兜孔。球形兜孔的加工难度较大,但能较好保证保持架强度。 测绘3#轴承公司所生产的其他调心滚子轴承实体保持架,发现做了诸多类似改进,例如,该公司24152MB轴承保持架外径也大于外圈端面与端面相交倒角后直径,该方案仍然采用整体保持架,但在保持架外径沿轴向方向往径向方向开缺口,综合考虑缺口的宽度与深度,实现整体保持架的装配。 通过对比国内外同型号调心滚子轴承参数可知,国内轴承设计方法优化的最小壁厚比国外大21%~35%。该参数大大限制了滚子直径(或滚子个数),降低了轴承的承载能力,因此减小最小壁厚可大幅提高调心滚子轴承的额定载荷。 从可靠性角度考虑,即使最小壁厚不变,也可借鉴国外设计经验,充分利用调心滚子轴承内部空间减少约束条件。 根据应用经验可知,采用现有真空脱气钢或电渣重熔钢,可将实体保持架调心滚子轴承的最小壁厚减小10%~20%。保持架不必拘泥于固定结构,可采用灵活的设计方法以增加主参数值。2.4 约束验算
3 主参数值对比

4 约束限制的调整

5 结束语
