基于小波包最优熵与RVM的滚动轴承故障诊断方法

2014-07-21任学平庞震辛向志邢义通马文生

轴承 2014年11期

任学平，庞震，辛向志，邢义通，马文生

(内蒙古科技大学机械工程学院，内蒙古包头 014010)

滚动轴承的使用寿命与工作优良程度往往制约着整个机械系统的运转状态。实际使用中，轴承受到冲击所产生的信号存在非平稳、非线性等特征，而且外界干扰噪声导致采集到的信号信噪比很低，难以提取故障特征。

轴承故障信号的时、频域分析方法是传统故障诊断主要手段，可以辨识轴承处于何种工作状态[1-2]，但均存在各自的局限性。支持向量机(Support Vector Machine，SVM) 具有良好的非线性区分能力，已广泛应用于故障诊断领域[3-5]。然而SVM也存在以下不足之处：(1)支持向量个数随训练样本数量成线性增加，从而导致过度调试并造成计算时间变长；(2)最终计算结果并非是概率式预测，分类的准确度很难进行认定；(3)需要多次人为主观猜测才能设定计算误差参数；(4)核函数K必须符合Mercer条件[6-7]。

为了弥补SVM的不足，提出了一种与其极为相似的稀疏概率方法，即相关向量机(Relevance Vector Machines，RVM)[8-10]。RVM与SVM有相同的数学表达式，但相关向量个数却远远小于支持向量个数，RVM的较高决策函数检测精度以及较短的计算时间增强了其实用性，已经很好地应用于各种分类处理问题[11-12]。

为了改善并进一步提高RVM 分类的准确率，分类前需要对数据进行预处理。因此，结合小波包最优熵对采集信号进行信号降噪分解预处理，提取各种故障状态下的特征向量，以提高后续RVM分类器的准确度。

1 基本理论

1.1 小波包特征提取原理

故障特征的提取主要是从难以分辨的时域信号中，运用不同信号处理方法提取可以表征不同设备状态的特征信息。小波包变换由小波变换延伸而来，具有很强的信号分析能力，不仅能对数据信号进行更精确地分解与重构，还可以提取任意时频段下的信号特征，在机械故障诊断中应用广泛。小波包节点能量比可以反映机械设备的工作状况[13]，可有效地作为信号特征，因此采用小波包最优节点熵能量作为故障信号特征。小波包变换基本定义为

(1)

(2)

(3)

对信号进行L层全小波包分解，可得到2L+1-2个节点，每个节点能量可有效表达本身特征，即得到2L+1-2个信号特征。信号特征通常从小波包分解后的最底层各节点能量提取，而在此依据信息花费最小原理[14]，对小波包分解得到的各节点系数运用香农熵的最佳基搜索算法寻求最优节点组合。以最优节点的能量构造特征向量，并为后续分析的方便进行归一化处理。

1.2 相关向量机

RVM主要以Bayes理论统计算法进行运算[15]，不仅可以处理向量回归问题，还很好地适用于向量分类问题，在此只运用其分类理论。

(4)

K(x,xi)=[1,k(x,x1),…,k(x,xN)]T，

w=[ω0,ω1,ω2,…,ωM]T，

式中：w为权值向量；K(x,xi)为核函数向量，当进行支持向量机运算时，其必须满足Mercer 条件，而相关向量机运算时K(x,xi)无需满足Mercer条件。

对于任意独立目标ti，其训练样本集的似然估计为

w)]}1-ti，

(5)

t=[t1,t2,…,tN]T。

根据概率预测公式，新的输入向量x*所对应的目标向量t*求得的条件概率为

(6)

运用最大似然法求解式中的w和σ2往往会引出过适应问题，且无法保障模型的稀疏性。为避免此现象，根据稀疏Bayes理论，给权值向量w分配独立的零均值Gauss先验分布，即

(7)

经过反复迭代计算可以得到所有权值，但发现绝大部分权值都变得很小，近似于零，只有很小一部分为非零权值，根据(4)式可知少量的非零权值才可以作为输入训练向量，即相关向量(Relevance Vectors，RVs) 。只保留相关向量后(6)式可改写为

dwdαdσ2。

(8)

2 故障诊断方法

根据小波包特征提取方法及RVM模型的建立，绘制的轴承故障诊断流程如图1所示。

图1 小波包最优熵与RVM故障诊断流程图

轴承故障诊断的具体步骤为：

(1)在正常、内圈故障、滚动体故障及外圈故障状态下，按一定的采样频率fs分别进行N次采样，共获得4N个振动信号作为样本。

(2)对每一种状态下的每个振动信号进行小波包降噪，降噪后进行小波包分解，得到各频段节点。

(3)对各频段节点进行熵值计算，以寻找最优节点作为研究对象。

(4)计算最优节点的能量

(9)

(5)构建能量特征向量

T=[E1,E2,…,Em]。

(10)

由于能量值较大，为便于分析处理，对T进行归一化后作为特征向量输入相关向量机。即

(11)

(12)

(6)建立由4个相关向量机(RVM1，RVM2，RVM3，RVM4)组成的多故障分类器。将轴承特征向量输入相关向量机，对相关向量机进行训练。

(7)采集测试信号，重新按照步骤(2)～(5)形成特征向量，并输入RVM进行分类，以RVM 分类器的输出确定轴承的工作状态和故障类型。

3 试验分析

试验采用美国Spectra Quest公司生产的机械故障综合模拟试验台，试验装置简图及传感器测点布置如图2所示。共采用3个加速度传感器：传感器1安置于齿轮箱轴承端盖的垂直径向；传感器2安置于齿轮箱轴承端盖的轴向；传感器3安置于齿轮箱轴承端盖的水平径向。

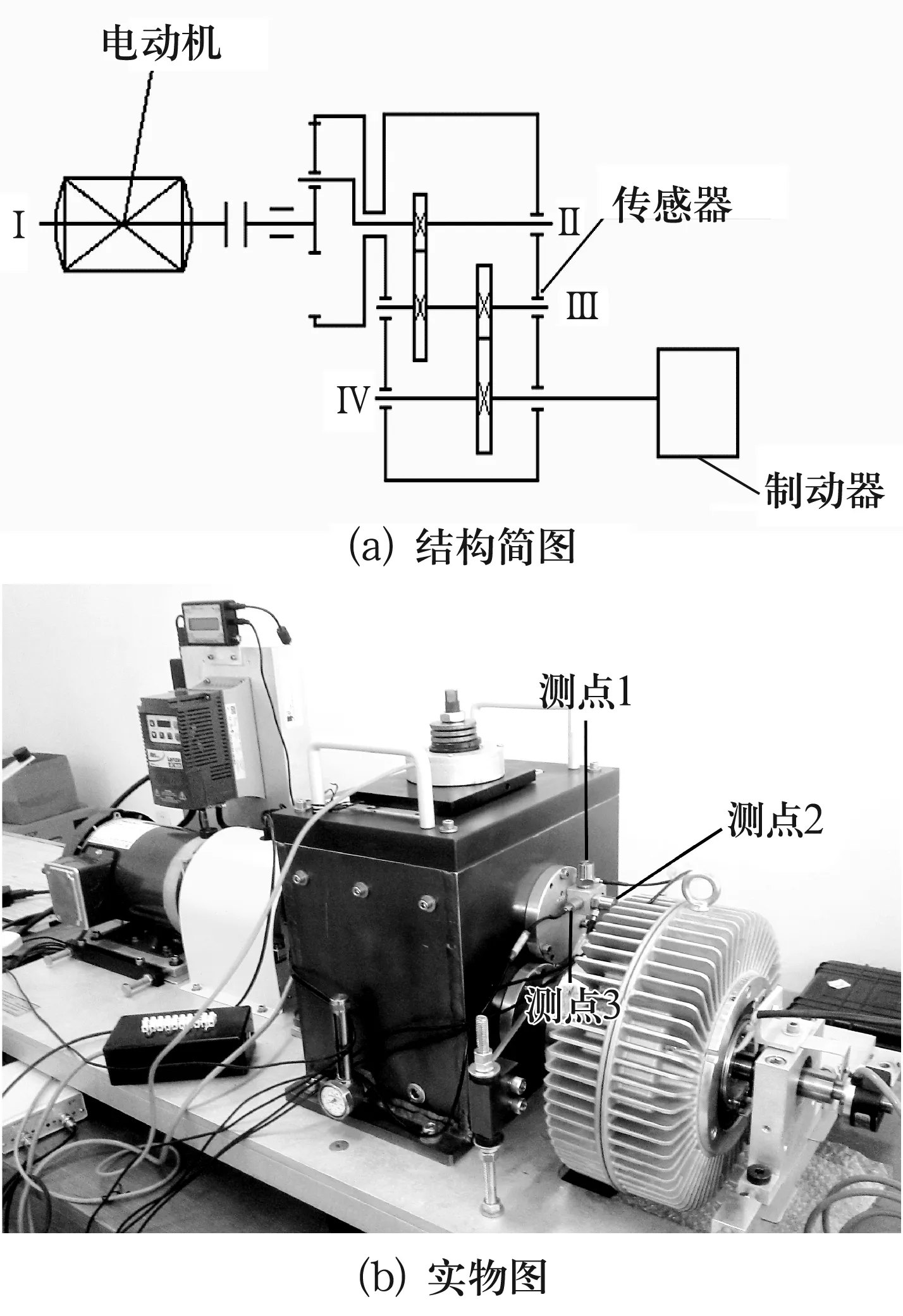
图2 试验装置简图

振动测试选用ZonicBook/618E便携式振动分析检测系统，可直接测量振动加速度和振动烈度(速度), 并进行实时状态监测和频谱分析，其信号数据采集原理如图3所示。试验采用圆柱滚子轴承减速器，轴承型号为美制ER-10K，其结构参数见表1。试验中外圈固定，内圈旋转，在承受一定载荷情况下进行不同转速的测试，振动信号由安装在轴承座上的加速度传感器提取。振动信号采样频率为2 560 Hz，分析频率为1 000 Hz，分析试验数据所使用的采样个数为2 048，采样时间为0.8 s。

图3 信号采集原理图

表1 试验轴承结构参数

对正常及内圈、滚子和外圈故障状态下的振动信号分别采样，各得40组数据。在4类数据中分别随机抽取30组数据作为训练样本，剩余数据作为测试样本。

首先对每组训练数据进行4层小波包降噪分解，得到30个节点分量；其次对各节点进行熵值计算并进行比较，找到最优小波包节点，构建最优小波包树；然后对最优节点进行排列，计算其能量并进行归一化处理；最后将归一化后的能量特征向量作为相关向量机输入的特征向量矩阵。转速为1 620 r/min时，小波包降噪前后的信号时域图如图4所示。由图4b可知，降噪效果十分理想，可以提高后续处理效率。

图4 降噪前后信号时域图

由于篇幅有限，以内圈故障信号为例，内圈故障信号降噪分解后各节点熵值见表2，根据信息花费最小原理选取最优小波包节点，构建的最优小波包树如图5所示。图中的节点(3，0)，(3，1)，(2，1)，(2，2)，(4，12)，(4，13)，(4，14)和(4，15)可以最有效、合理地体现原始振动信号信息。对4种状态信号的最优节点进行排列并计算其能量分布，结果如图6所示。由于节点能量值过大会增加后续计算量，需对其进行能量归一化处理。

表2 内圈故障信号各节点熵值

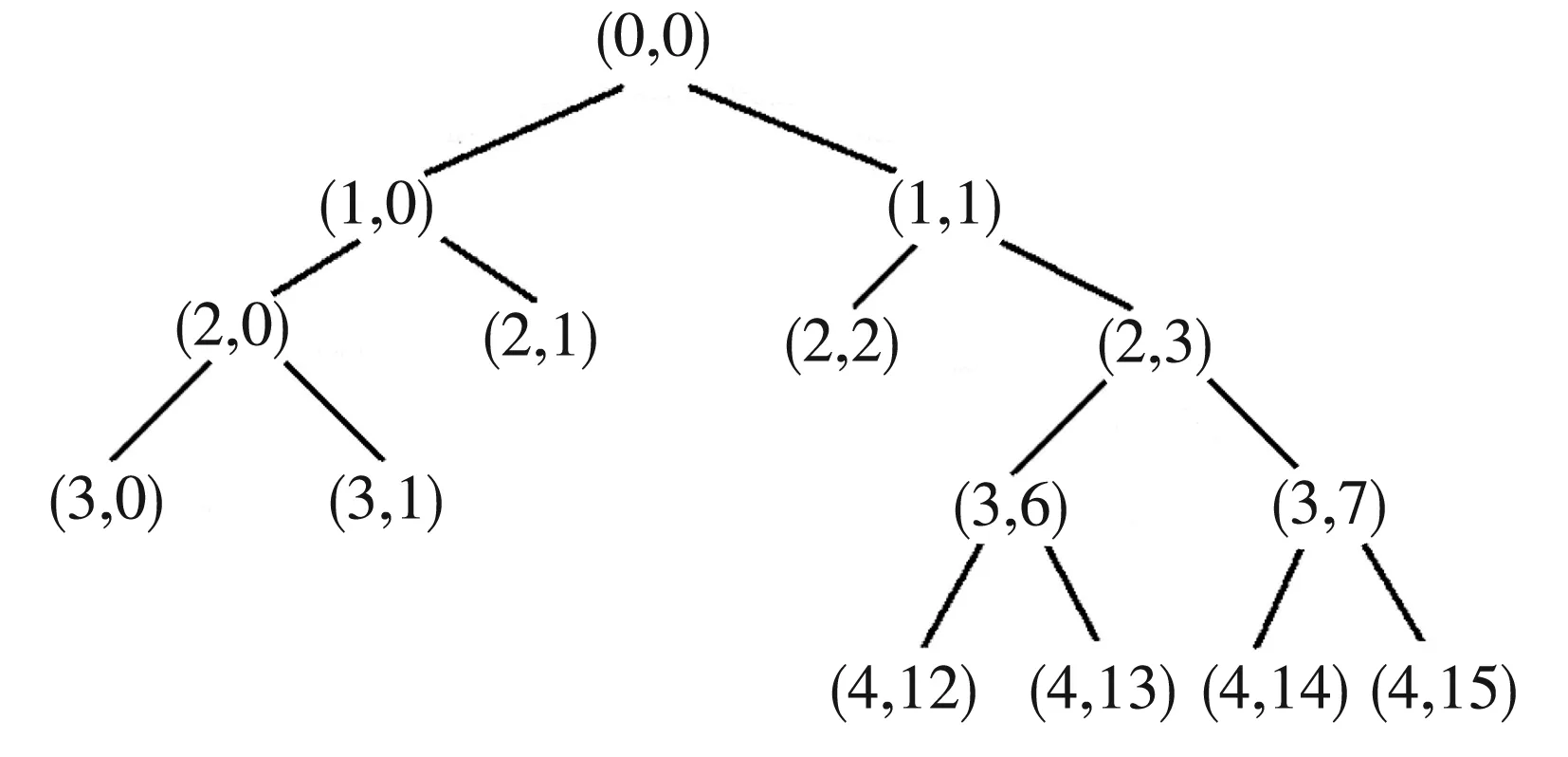
图5 最佳小波包树

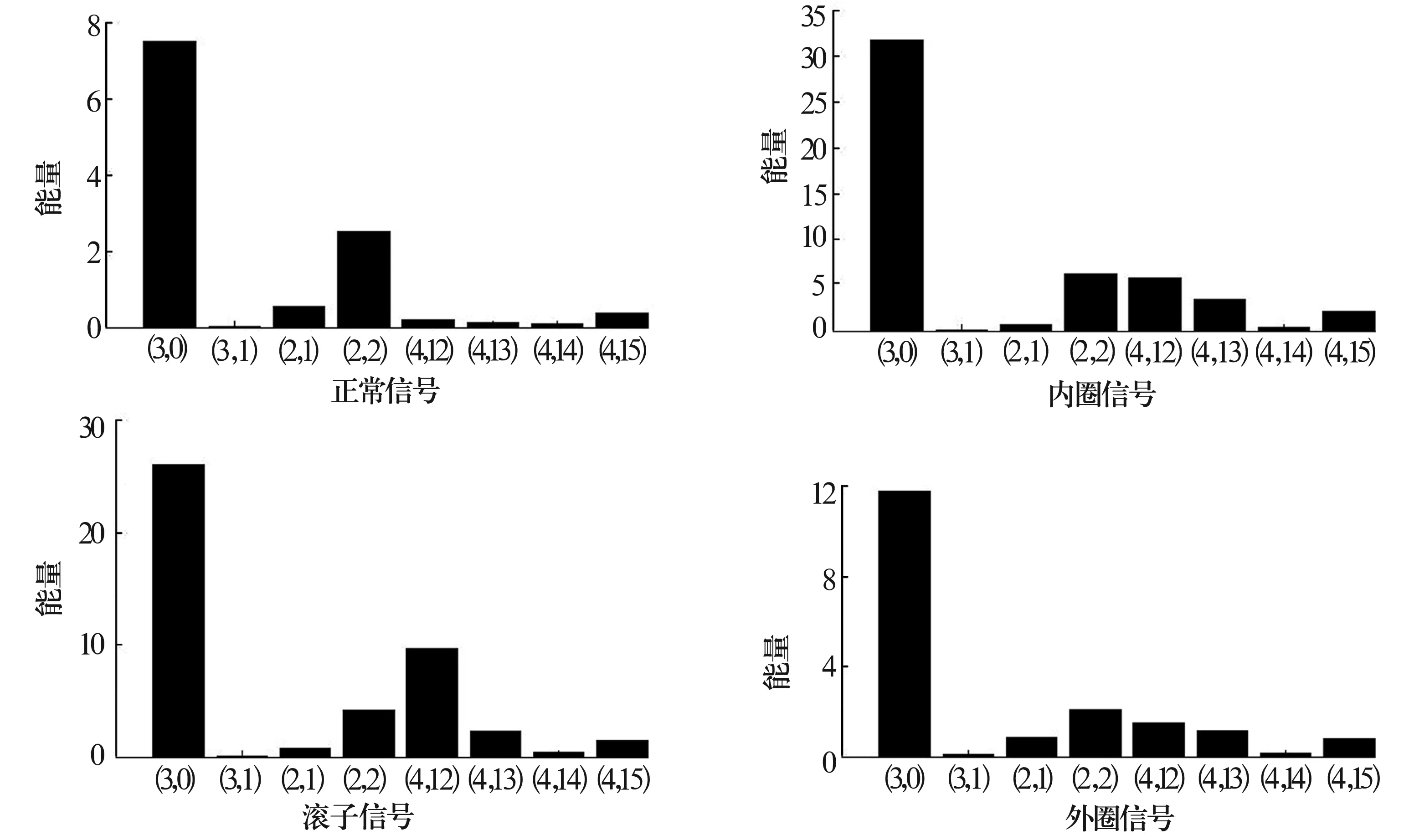
图6 小波包节点能量分布图

每种状态信号的3组特征向量见表3。将提取出来的特征向量输入到由4个相关向量机组成的多故障分类器中进行训练。最后，将每种状态振动信号中剩余的10组同样计算出特征向量，输入已经训练好的相关向量机中进行故障的模式识别，结果见表4。由表4可知，对于测试样本，相关向量机的正确率很高。

表3 RVM多故障分类器的训练样本表

表4 相关向量机测试结果

为证明小波包最优熵和相关向量机算法的优越性能，进行了小波包-神经网络(WP-BP)、小波包-支持向量机(WP-SVM)、小波包-相关向量机(WP-RVM)和小波包最优熵-相关向量机(WPOS-RVM)的试验比较。试验选取30组原始振动加速度信号进行处理(数据量属于小样本情况)，结果见表5。通过数据对比可以看出，RVM比BP与SVM的训练时间短，并且与小波包最优熵的结合提高了测试精度，具有良好的推广能力。