整体式气浮导轨的等间隙设计方法

宋伟，张君安

(西安工业大学 机电工程学院，西安 710021)

用多个气浮垫装配动导轨时，气浮垫用球铰支撑，这样可以自找准平衡位置，保持气膜间隙相等，不过需用到滑架，这时动导轨的体积大承载能力小(图1)[1]。而用整体式导轨装配动导轨时，动导轨的体积小承载能力大(图2)[2]。目前使用气浮导轨工作时，在设备的位置坐标以及承载力的计算方面，坐标的标定都是基于气膜为等间隙的状态。由于整体式气浮导轨与工作装置的连接通常是固定的，因而气膜间隙越趋于平行，工作精度越高。但工作过程中，整体式气浮导轨由于受到载荷或惯性力的作用，必然会产生偏载，导致导轨间隙不相等，即导轨的运动平面与固定平面不平行，从而产生偏角，直接改变了与导轨固连装置预期的空间坐标(如圆柱度测量仪的触头，砂轮修形器的金刚笔等)。这种偏角也会使导轨的承载力发生变化，并且由于气膜厚度很小，很小的偏角就有可能引起刮蹭，影响轴承稳定性。

图1 分离式气浮垫导轨简图

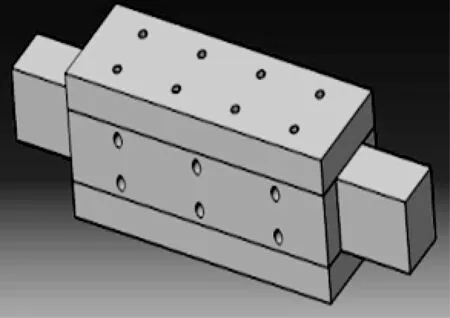
图2 整体式气浮导轨简图

如果能对导轨加一个预偏角，来抵消加工过程中由外载产生的偏角，从而恢复等间隙状态，就可以大大提高导轨稳定性及其加工精度。整体式气浮导轨的等间隙设计方法就是通过同时约束承载力与偏载力矩，对多节流孔整体式气浮导轨的各节流孔内径进行设计，从而控制气体压力分布，对偏载力矩进行预补偿，解决偏角问题，进而从理论上消除整体式气浮导轨的工作误差，提高其工作精度。

1 等间隙设计原理

如图3所示，可将气浮导轨偏载简化为斜面中心点的合力F，以及两个坐标的偏载力矩Mx，My。图中n1，n2为两个斜面的法线，夹角为θ，即为文中要讨论到的偏角。

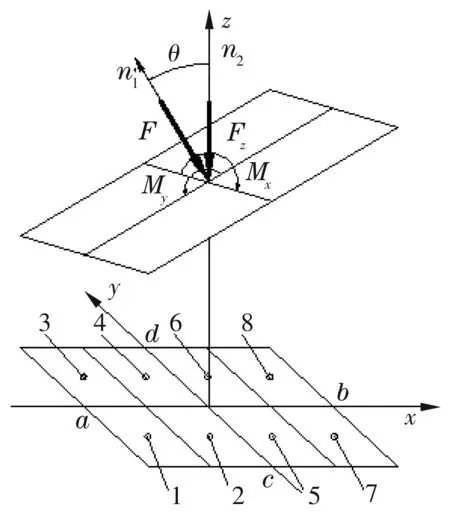
图3 导轨受偏载简图

由图3可见，外载垂直于斜面，而非竖直向下。故可将F分解为水平力和竖直力。而水平力不会在此产生偏载，因而，要抵消偏载使导轨保持水平，可只讨论竖直力Fz。由静力学可知，气膜压力提供的承载力应该等于Fz。而气体压力对x轴，y轴的总力矩应分别等于Mx，My。利用气体质量守恒原理确定的连续条件[3]，可算出偏载时各节流孔出口压力[4]，通过Reynolds方程可得到偏载时的压力分布，对其积分可得到Fz，Mx，My。

如图4所示，再通过反推法：先令气浮导轨两平面平行，根据Reynolds方程，算出此时各节流孔出口压力，与上述得到的一组节流孔出口压力进行比较，得出每个节流孔出口压力变化量；按其大小进行排序，为每个节流孔设定不同的步长，同时调节8个节流孔出口压力，对承载力和偏载力矩进行耦合，直到使等间隙条件下得到的F1，Mx1，My1能与偏载状态下的Fz，Mx，My分别相等；最后确定满足承载力与偏载力矩约束条件的一组节流孔出口压力，根据气体质量守恒原理，可算出各孔内径值，进而解决给定偏载下承载面的偏角问题。

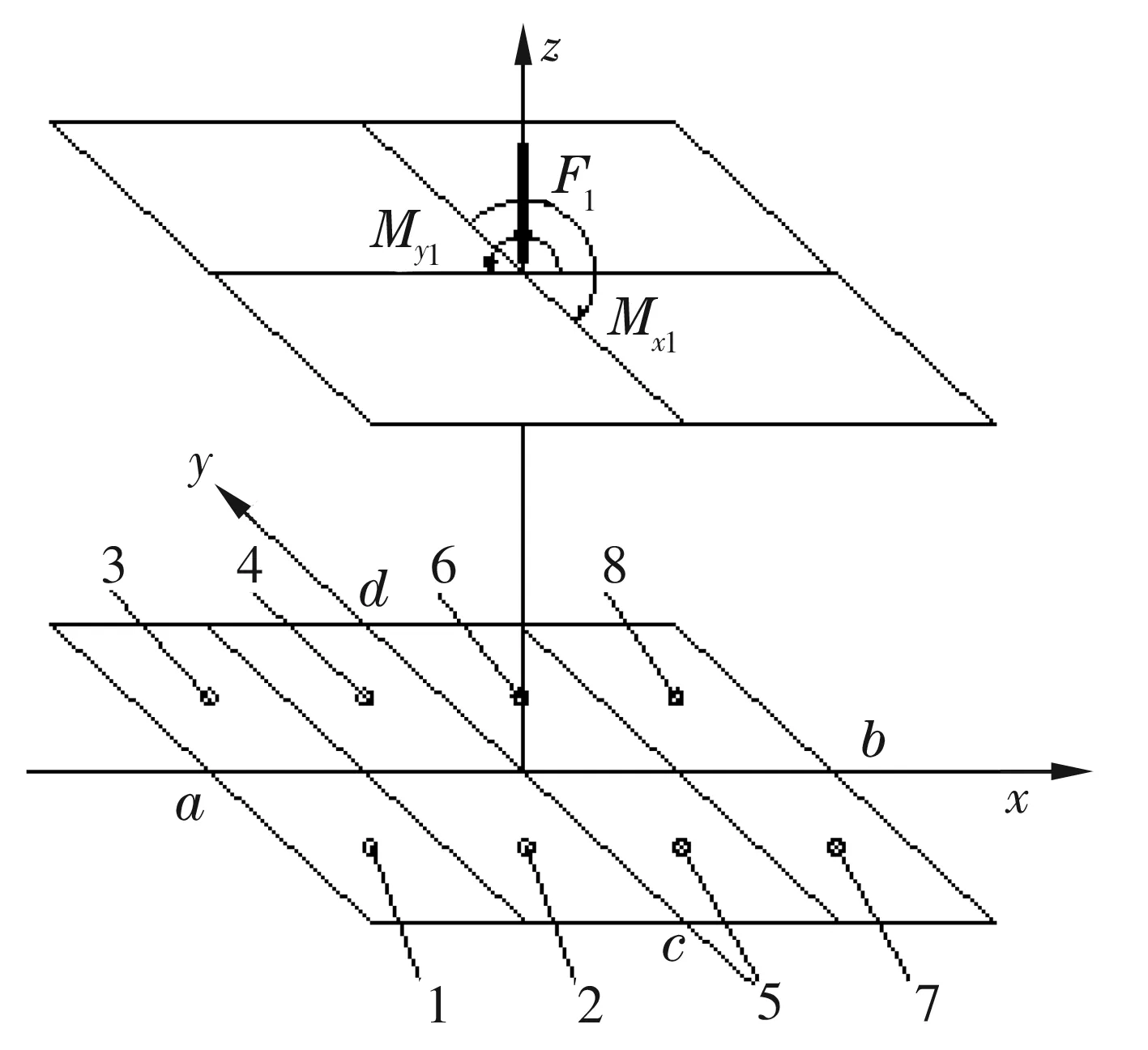
图4 校正后的导轨受力简图

2 控制方程

2.1 Reynolds方程

Reynolds 方程是整个气体润滑力学的核心，流体润滑的基本内容均是求解 Reynolds 方程以揭示流体润滑膜中压力的分布规律。决定压力分布的方程式可由 Navier-Stokes方程和连续方程经过润滑条件下的近似处理推导而得到。文中假设气浮导轨为静态，系统为定常状态，将Reynolds方程简化后得[5]

(1)

式中：p为气膜中气体压强，h为气膜厚度。

2.2 流入轴承承载气膜气体流量

如图4所示，气浮垫承载气膜的流量win1～win8的计算公式为[4]

(2)

式中：R为气体常数；C0为喷嘴流量系数；P0为节流孔的出口压力；Ps为供气压力；T0为供气温度；k为绝热指数；ψi为第i个供气孔的流出速度系数；di为第i个供气孔的直径；hii为第i个供气孔处的气膜厚度；(win)i为第i个供气孔的流入流量。

加强和改进镇街人大工作，党委重视、组织保障是关键，营造氛围、形成共识是前提，务求实效、服务中心是目的。

2.3 流出的气体质量

(3)

式中：h为气膜与大气边界处的间隙，a，b为导轨在x轴方向长度，c，d为导轨在y轴方向长度。

3 数值分析求解

3.1 有限差分法解Reynolods方程[6]

令f=p2，代入Reynolods方程，得

(4)

对于中间点用中心差分，得到

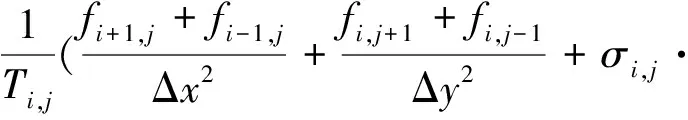
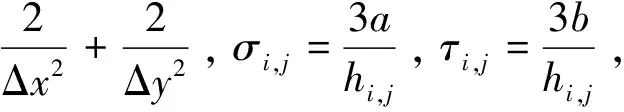
(5)

再利用超松弛迭代就可求出(1)式。此处选用的差分都为二阶精度。

3.2 边界条件

如图3与图4所示，假设导轨四周与大气相接，则x=a，x=b时，p=pa；y=c，y=d时，p=pa，其中pa为大气压强。

3.3 辛普森公式

如图4所示，设x，y平面区域为D，并把x轴长度分为m份，把y轴长度分为n份，根据已算出偏载时各节流孔出口压力[4]，通过Reynolods方程可得到压力分布p(i,j)。设斜面中心O点气体压强为po，pa为标准大气压，可根据以下公式得到Fz，Mx，My，即

(6)

(7)

从而推出双重积分展开公式为

(8)

括号中3项分别用辛普森公式展开

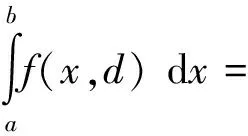
(9)

最终可得

(10)

如果令f(x,y)=p(i,j)-pa，然后把上面公式中的a,b,c,d长度分别用±dx,±dy来代替可得

(11)

相当于把整个平面由坐标原点开始，分成很多个由9个点组成的小区域，根据(11)式可以算出每个小区域的承载力。然后根据i，j的循环语句进行叠加计算出整个面上的承载力。令f(x,y)=[p(i,j)-pa]x，或f(x,y)=[p(i,j)-pa]y可分别求得对y轴和x轴的力矩，辛普森展开式这里不再列举，与求承载力方法相同。此处辛普森公式具有三次代数精度。

4 实例与分析

以图2所示导轨的下部气膜为例，设此气膜在导轨受偏载状态下，上、下表面如图3所示，而在校正为等间隙气膜以后，气膜的上、下表面如图4所示。为了在理论上准确地分析偏载对气浮导轨的影响，以气膜间隙为5 μm 为例，计算在极小气膜间隙情况下，将不同偏角的气浮导轨调整为等间隙导轨时所对应的各节流孔内径设导轨的x方向边长为120 mm，y方向边长为60 mm，双排8个固有孔节流供气配置，8个节流孔序号如图4所示，孔径d=0.1 mm。设润滑气体为常温空气，供气压力Ps=0.6 MPa，动力黏度μ=1.833×10-10kgs/cm2，绝热指数k=1.4，密度ρ=1.226×10-16kg/cm3，气体常数R=29.27 m/K，常温T=288 K，喷嘴流量系数C0=0.85。取x，y方向的网格划分数m=40，n=20，取σ=10-4，误差流量ε=3%，得到3种偏角下的节流孔内径设计结果如下：

(1)如图5所示，校正偏角为0.001 1′时,节流孔内径d1=0.202 mm，d2=0.309 mm，d3=0.131 mm，d4=0.066 mm，d5=0.254 mm，d6=0.049 mm，d7=0.079 mm，d8=0.058 mm。此时承载力1 479 N。

(2)如图6所示，校正偏角0.002 9′时，节流孔内径d1=0.989 mm，d2=0.754 mm，d3=0.136 mm，d4=0.035 mm，d5=0.203 mm，d6=0.044 mm，d7=0.069 mm，d8=0.049 mm。承载力为1 439 N。

图6 偏角为0.002 9′时,校正前、后的平面图与压力分布图

(3)如图7所示，校正偏角0.004 1′时，节流孔内径d1=1.405 mm，d2=1.637 mm，d3=0.408 mm，d4=0.051 mm，d5=0.888 mm，d6=0.009 mm，d7=0.089 mm，d8=0.009 mm。承载力为1 407 N。

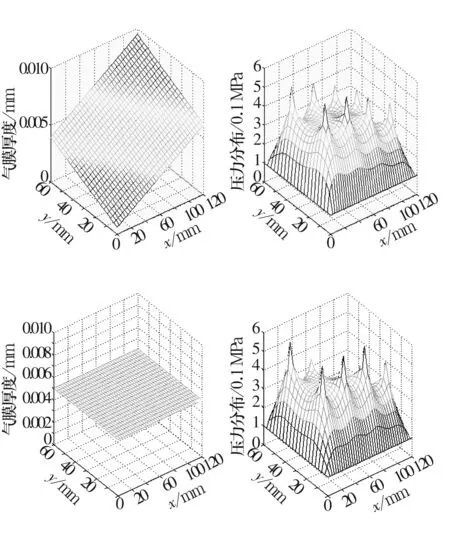
图7 偏角为0.004 1′时，校正前、后的平面图与压力分布图

由以上3种偏载情况可以得出：

(1)由于气膜厚度相对于xy平面长度非常小，极小的偏角在整个平面上能产生较大的倾斜，如上述3个例子中偏角都不超过0.003′，但平面的倾斜就已经很明显了，所以不能因为倾斜角度小而忽略由此造成的误差。

(2)显然以气膜中心厚度为5 μm为基准，承载力会随着偏角的变化而变化，并且轴承的倾斜角越大，气浮垫损失的承载力就越多。在超高精度加工中如果盲目的用等间隙情况下的承载力来代替偏载时的承载力就会导致计算误差，并且误差会因偏载角度的增大而增大。

(3)对比3个实例可知，校正后的气膜压力分布不如偏载时那么均匀。这是因为把斜面校正成等间隙平面后，本来气膜厚度低的地方变高，而厚度高的地方变低。根据Reynolods方程，原来压力较大的区域整体压力变小，而原来压力较小的区域整体压力变大，导致偏载力矩发生变化。要保证导轨调平以后承载力和力矩都不变，就要增大被减小区域的节流孔出口压力，从而增大其所在区域的整体压力，同理则应减小被增大区域的节流孔出口压力。这样在承载力不变的条件下对力矩进行了补偿，因而校正后的压力分布图显得更尖锐陡峭，不如校正前平缓。

5 结束语

通过设计节流孔内径，解决了整体式气浮导轨由偏载所产生的偏角带来的生产误差问题，从理论角度得到了一套实现对整体式气浮导轨等间隙调平，提高气浮导轨的工作精度和稳定性的方法。

经数值分析的结果可知，即便是5 μm的气膜间隙，偏角在0.003′以内，气膜承载力也会随偏角的增大而减小近100 N，这也说明了在偏载状态下，气浮导轨的误差不仅仅影响工作精度和稳定性，也会造成承载力的损失。

由于文中方法是基于理论上对气膜间隙的精确调平，在生产加工时存在一定的局限性：当偏角过大时，理论得出的节流孔内径设计方案会由于某些节流孔内径过小而难以加工，所以在大倾斜度的情况下，要通过变节流孔内径来对斜面进行严格的调平，以目前的生产水准来说很难实现。用此方法可以得到各节流孔内径比例关系，在生产能力许可的条件下，对节流孔进行改造，虽不能完全根据计算结果的要求生产超小内径节流孔，但仍能实现减小偏载倾斜度的目的。