ε-近似保内积的某个特定值映射

孔亮

（商洛学院 数学与计算机应用学院，陕西商洛726000）

ε-近似保内积的某个特定值映射

孔亮

（商洛学院 数学与计算机应用学院，陕西商洛726000）

在复Hilbert空间中给出了近似保内积的某个特定值映射的定义，研究了近似保内积的某个特定值线性映射的性质，应用复Hilbert空间中的平行四边形法则证明了非零近似保内积的某个特定值线性映射是有界且下有界的，推广了近似保正交线性映射的定义和结论。

Hilbert空间；正交；近似正交；特定值映射

Hilbert空间中的正交性是泛函分析的重要概念之一,由正交性定义的正交基、投影算子等概念，丰富了Hilbert空间理论，从而是研究Hilbert空间的重要工具。一般赋范空间几何性质的研究，在20世纪初得到了很大的发展，各种正交性概念被相继引入[1-3]。近年来，保持各种正交和近似保持各种正交映射的性质，得到了众多学者的深入研究：Chmieliński J[4]在内积空间给出了保正交线性映射的刻画,Chmieliński J[5]在有限维内积空间中给出了保正交线性映射的稳定性，Blanco A等[6]在赋范线性空间中证明了保正交线性映射是等距的常数倍，Turns'ek A[7]研究了与正交定义有关的稳定性问题，Chmieliński J[8]在一般的Hilbert空间推广了文献[5]的结果，孔亮等[9]在赋范线性空间中给出了近似Birkhoff正交的定义和性质，Ilis'evic D等[10]在Hilbert空间中给出了一个新的近似保正交映射的定义和性质，孔亮等[11]将文献[7]的结果推广到准Hilbert C*-模上，Chmieliński J等[12]在Hilbert空间中给出了映射是ε-近似保正交映射的充分条件并得到了ε-近似保正交映射的扰动定理,Mojkerc B等[13]在实赋范线性空间中给出了近似保等腰正交映射的刻画[14-17]。关于其它各种近似保正交映射已有许多研究。受文献[1-17]概念和结果的启发,本文在复Hilbert空间中引入ε-近似保内积的某个特定值映射的定义，证明非零近似保内积的某个特定值线性映射是有界且下有界的，推广了ε-近似保正交线性映射的定义和结论。

1 预备知识和结论

H和K在本文中均表示复Hilbert空间，〈.，.〉是它们的内积,i是虚数单位，R表示实数集，C表示复数集。

定义1[8]设x,y∈H，若〈x,y〉=0则称x和y是正交的，记为x⊥y。

定义2[8]设x,y∈H，ε∈[0,1)，若｜〈x,y〉｜≤ε｜x｜｜y｜，则称x和y是近似正交的，记为x⊥εy。

定义3[8]设x,y∈H，ε∈[0,1)，若映射T：H→K满足x⊥y⇒T(x)⊥εT(y)，则称T是ε-近似保正交的。

定义4设x,y∈H,c∈[0,1],ε∈[0,1),若映射T：H→K满足

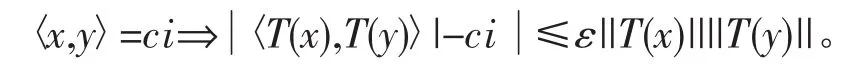
则称T是ε-近似保内积的某个特定值。

注1特别地，在定义4中令c=0，则得〈x,y〉=0⇒｜〈T(x)，T(y)〉｜≤ε｜T(x)｜｜T(y)｜，则T是ε-近似保正交映射。从而定义4是定义3的一个推广。

文献[7]给出了关于ε-近似保正交线性映射的结论：

定理1[7]设ε∈[0，1),T：H→K是ε-近似保正交线性映射，则T有界且满足本文主要得到以下结论：

定理2设c∈[0，1],ε∈[0，1],T：H→K是ε-近似保内积的某个特定值线性映射，则T有界且满足

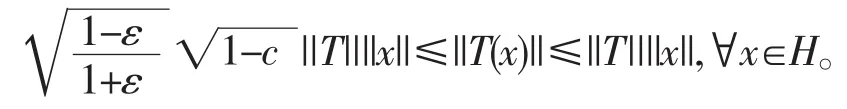
注2因为由注1可知当c=0时，ε-近似保内积的某个特定值的线性映射就是ε-近似保正交线性映射，所以在定理2中令c=0,即得定理1。即定理2是定理1的一个推广。

2 结论的证明

为了完成定理2的证明,先给出2个引理。

引理1设x,y∈H，c∈[0,1],ε∈[0,1),若

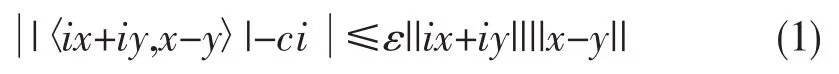
定理2的证明对于H中的任意单位向量u,v，

[1]Roberts B D.On the geometry of abstract vector space[J].Tohoku Math J,1934,39：42-59.

[2]Birkhoff G.Orthogonality in linear metric space[J].Duck Math J,1935,1(2)：169-172.

[3]James R C.Orthogonality in normed linear space[J].Duck Math J,1945,12(2)：291-302.

[4]Chmieliński J.Linear mappings approximately preserving orthogonality[J].J Math Anal Appl,2005,301(1)：158-169.

[5]Chmieliński J.Stability of the orthogonality preserving property in finite-dimensional inner product spaces [J].J Math Anal Appl,2006,318(2)：433-443.

[6]Blanco A,Turns'ek A.On maps that preserve orthogonality in normed spaces[J].Proc Roy Soc Edinburgh Sect A, 2006,136(4)：709-716.

[7]Turns'ek A.On mappings approximately preserving orthogonality[J].J Math Anal Appl,2007,336(1)：625-631.

[8]Chmieliński J.Remarks on orthogonality preserving mappings in normed spaces and some stability problems[J].Banach J Math Anal,2007,1(1)：117-124.

[9]孔 亮,曹怀信.保正交映射与正交性方程的稳定性[J].陕西师范大学学报：自然科学版，2008,36(5)：10-14.

[10]Ilis'evic D,Turn s'ek A.Approximately orthogonality preserving mappings on C*-modules[J].J Math Anal Appl,2006,318(2)：433-443.

[11]孔 亮,曹怀信.ε-近似保正交映射的稳定性与扰动[J].数学学报,2010,53(1)：61-66.

[12]Chmieliński J,Wójcik P.Isosceles-orthogonality preserving property and its stability[J].Nonlinear Anal,2010,72(8)：1445-1453.

[14]Kong L,Cao H X.On linear mappings approximately preserving orthogonality[M]//Proceeding of the seventh international conference of matrices and operators.Edgbaston：World Academic Press,2012：20-23.

[15]Wójcik P.Linear mappings preserving ρ-orthogonality [J].J Math Anal Appl,2012,386(1)：171-176.

[16]Burgos M.Orthogonality preserving linear maps on C*-algebras with non-zero socles[J].J Math Anal Appl,2013,401(2)：479-487.

[17]孔 亮.ε-近似保等腰正交线性映射的刻画[J].海南大学学报,2013,31(3)：193-198.

(责任编辑：李堆淑）

On Mappings Approximately Preserving a Particular Value of Inner Product

KONG Liang
(College of Mathematics and Computer Application,Shangluo University,Shangluo 726000,Shaanxi)

In complex Hilbert spaces,the definition of mapping approximately preserving a particular value of the inner product is given.Then the properties of linear mapping approximately preserving a particular value of the inner product are studied.Finally,it is proved that the nonzero linear mapping approximately preserving a particular value of the inner product is bounded and bounded below by parallelogram law.The result is a generalization of approximate orthogonality preserving linear mappings.

Hilbert space;orthogonality;approximate orthogonality;particular value of the inner product

O177.1

：A

：1674-0033(2014)06-0013-03

10.13440/j.slxy.1674-0033.2014.06.005

2014-04-29

商洛学院科研基金项目（14SKY016）

孔 亮，男，陕西商州人，硕士，讲师