永磁电动机转子温度场数值计算

王 磊

(黑龙江工业学院，黑龙江鸡西 158100)

一 永磁电机转子温度场求解模型的确定

本文主要依据传热学的基本理论，根据电动机的结构特点，在基本设计的基础上建立了电动机转子温度场的求解模型以及相应的数学模型，并结合边界条件，采用有限元法对电动机转子温度场进行数值求解。

1.基本假设及求解域确定。

永磁直流电动机如上所述具有结构简单、起动性能好以及转子机械强度高等优点，使其成为新型永磁电机领域的研究热点。在稳态运行条件下，由于定子开槽，定子齿在转子表面会产生磁通脉动分量，当电枢相对于转子运动时会产生涡流，并产生损耗和发热问题。这直接关系着永磁体的退磁问题和永磁电机的工作性能。因此准确计算永磁电机的温度场对于电机的设计和分析具有重要的指导意义。

目前关于电机温度场计算的文献较多，但是未见涉及实心转子永磁同步电机温度场方面的文献，这主要是因为这种电机较为新颖，而且其转子结构复杂，各部分损耗的确定十分困难。本文借鉴了水轮发电机实心磁极表面附加损耗的计算方法来确定转子表面的损耗，建立二维温度场的数学模型，准确计算转子各部分温度分布，解决了确定永磁电机温度分布的难题。

本文中的永磁电动机采用全封闭外置风扇冷却结构，内部无通风系统。为了确定电动机转子温度场的求解域，需要给出如下的基本假设:

(1)认为电机沿轴向的热流密度为零，故可将三维温度场问题转化为二维温度场问题求解分析，从而简化计算难度和节省计算时间;

(2)隔磁环和转轴之间没有热传递;

(3)转子表面损耗集中在一个透入深度内。

由以上的基本假设，可以取电动机转子轴向中心截面为电动机转子温度场的求解域，如图1所示。

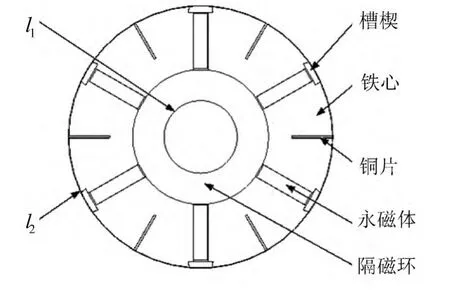
图1 电机温度场求解域模型

在图1中，标出了永磁电动机不同部位的名称，且所示的区域为转子铁心内表面，而区域表示转子铁心外表面。

二 数学模型及相关因素的确定

在给定电动机转子温度场求解域的基础上，要想准确地求解温度场中的温度数值，还要借助相应的数值方程和数值计算方法。

1.求解方程与边值条件。

根据以上的基本假设，对于各向同性媒质，导热系数为常数，在直角坐标系下的二维稳态热传导方程为:

式中 T—待求温度(℃);

λ—材料的导热系数(W/(m·K));

qv—热源密度(W/m3)。

根据假设条件，对转子铁心内表面给出第二类边界条件:

式中n—转子表面单位法向矢量。

电动机转子表面通过对流散热，可以给出第三类边界条件:

式中 α—散热系数(W/(m2·K));

Tf—气隙内冷却空气的温度(℃)。

从而求解域内二维稳态温度场微分方程以及边值问题可以综合表示为:

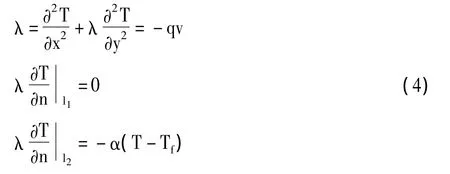
由变分原理可知，给出式(4)的泛函:

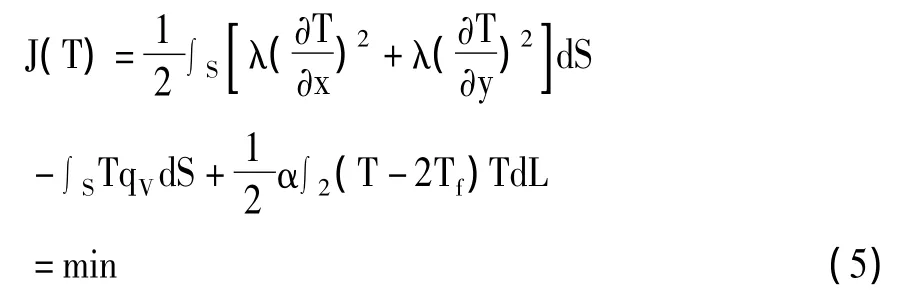
式中 S—求解域。

式中 T—求解域内全部节点温度所形成的温度列阵;

K和F—分别为总体系数矩阵和总体右端列矢量。

再将边界条件代入上式修改，最终获得一个线性方程组，解此方程组即可得到各个节点的温度值。

2.转子表面散热系数的确定。

转子的旋转带动气隙中空气的流动，使得转子与气隙之间主要以对流方式换热，导致了温度场与流体场耦合在一起，增加了求解电机温度场的难度。

为简化计算分析，引入有效导热系数λeff(W/(m·K))，它是用静止流体的导热系数来描述气隙中流动空气的热交换能力，即单位时间内静止流体在转子表面所传递的热量和流动空气所传递的热量相等，这样可把旋转的转子视为静止不动处理。从而可以用导热方式换热的效果等价气隙中对流方式换热的效果。

假设定子内表面和转子外表面为光滑圆柱面，由于电机内没有轴向通风，气隙中的雷诺数可表示为下式:

式中 ωφ1—转子的圆周速度(m/s)，其中 ωφ1=2πn·r0/60，n为转子的转速(r/min)，r0为转子的外径(m);

δ—气隙长度(m);

υ—空气的运动粘度(m2/s)。

临界雷诺数Recr的表达式为:

式中Ri—定子的内径(m)。

(1)当Re＜Recr，气隙中的空气流动为层流，有效导热系数λeff等于空气的导热系数λair;

(2)当Re＞Recr，气隙中的空气流动为紊流，这种状态下，气隙的有效导热系数可用下式计算。

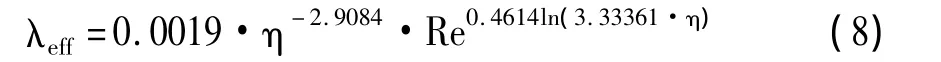
式中η=r0/Ri。

(3)转子表面附加损耗的计算。

在永磁直流电动机中，由于绕组非正弦分布，受定、转子齿槽效应的影响，电机气隙中存在一系列高次谐波磁场，这些高次谐波磁场会在实心转子表面产生附加损耗。根据电磁场理论，可得空载额定电压时实心转子表面的附加损耗，即:

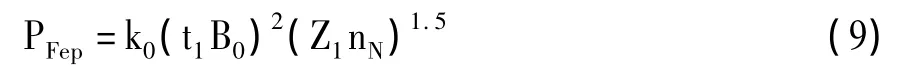
式中k0—计算表面损耗所用的系数，与磁极材料性质有关;

t1—定子齿距(m);

B0—齿谐波最大磁通密度(T);

Z1—定子槽数;

nN—同步转速(r/min)。

若将由定子各次相带谐波磁势产生的各次相带谐波磁场的磁密幅值、定子齿距等参数代入式(9)，然后相加，即得到有这些谐波在转子表面产生的附加损耗P2vk。对于三相电机表面损耗有:

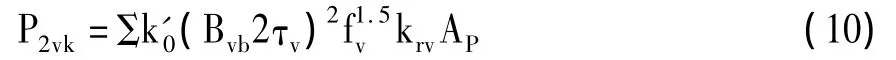
式中v=5，7，11……;k＇0=k0(60)1.5;

fv—定子v次相带谐波在转子表面感应电势的频率(Hz);

Ap—为转子表面积(m2);

Bvb—V次相带谐波磁势所产生的同次谐波磁密幅值(T)，等于:

式中μ0—空气磁导率(H/m);

kdpv—绕组系数;

A—线负荷(A/m);

krv—考虑涡流作用下的系数。

由以上的推导，可得:

把定子绕组磁势中高次谐波磁场有关量代入式(10)，进一步整理、化简并修正得到负载时定子绕组磁势中高次谐波在转子表层产生的附加损耗的计算公式如下:

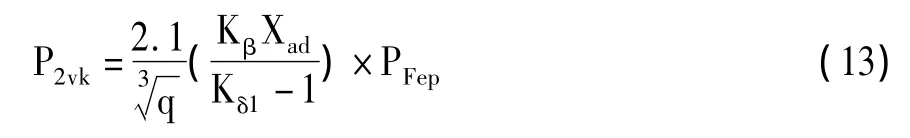
式中q—每极每相槽数;

Kβ—与短距系数有关的计算系数;

Kδ1—定子齿的气隙系数;

Xad—直轴电枢反应电抗。

电动机负载时，除了定子绕组高次谐波磁动势在转子磁极表面产生附加损耗之外，还有定子齿谐波磁动势在转子表面产生的附加损耗。根据电磁场理论，齿谐波磁通密度的幅值为:

式中kvt—空间衰减系数，对一阶齿谐波次数，因此空间衰减系数的表达式为:

把定子齿谐波磁场有关量代入式(10)，并考虑涡流对磁场的削弱作用，进一步整理、修正得到定子磁场中齿谐波在转子表层产生的附加损耗计算公式如下:

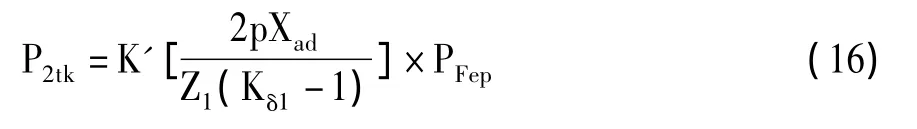
式中p—电动机的极对数;

K＇—最大气隙长度比系数。

在电机内损耗的确定方面，利用第二章的三维电磁场的基本方法对电内的电磁损耗进行分析求解，并且在电机内温度场的数值求解中作为热源项施加到求解模型中，采用有限元法获得电机内的温度分布特性。

［1］张新波，许承千.电机三维温度场的综合分析［J］.电工技术杂志，2000(3):4－6.

［2］范永达，苏文印.大型汽轮发电机转子温升计算［J］.大电机技术，1990(5):14 －16，55.

［3］曹国宣.水内冷汽轮发电机转子温度场计算［J］.电工技术学报，1993(1):18 －21，17.