带有 Kenics静态混合器的水平液固循环流化床颗粒分布的数值研究

刘 燕，张丽梅，张少峰，杜亚威

（ 1. 河北工业大学 海洋科学与工程学院，天津 300130；2. 河北工业大学 化工学院，天津 300130）

带有 Kenics静态混合器的水平液固循环流化床颗粒分布的数值研究

刘 燕1，张丽梅2，张少峰1，杜亚威1

（ 1. 河北工业大学 海洋科学与工程学院，天津 300130；2. 河北工业大学 化工学院，天津 300130）

利用 STAR-CCM+软件建立 Eulerian-Lagrangian 模型，对带有 Kenics 静态混合器的水平管内低浓度液固两相流动时的颗粒分布进行了数值模拟，考察了液体流速、Kenics 静态混合器扭率、颗粒体积分数对水平管中颗粒分布的影响．结果表明：Kenics 静态混合器的加入能够很好地改善水平管内颗粒径向分布不均匀情况，且扭率越大，效果越明显；流速的增大和颗粒体积分数的增加都可以改善颗粒固含率径向分布不均匀情况．同时通过和文献中的实验结果进行比较，验证了所选模型的可靠性．

液固循环流化床；Kenics 静态混合器；颗粒分布；数值模拟；水平管

0 前言

液固循环流化床换热器是将流化床技术与换热技术相结合而发展的一种设备，具有较好的防除垢效果、强化传热、易操作等优点，在化工、石油、污水处理等众多工业领域都有广泛应用，国内外学者也因此对其进行了深入的研究[1-5]．

但上述研究的对象多是针对竖直方向液固循环流化床进行的，关于水平方向则很少见诸文献．不同于竖直管流化床，水平液固循环流化床中因颗粒受到重力作用，使其流动具有自身特点，即颗粒极易沉积在水平管底部，导致颗粒分布不均匀现象，影响流化床性能，因此如何使颗粒在水平管液固循环流化床中均匀分布成为影响水平流化床稳定发展的关键．

在流化床中加入改善颗粒分布的装置是一种行之有效的方法．Kenics 静态混合器[6]结构简单、成本低廉、制造安装方便，且对单相流、两相流都有良好的混合能力，被广泛应用于石油、化工等行业中流体的混合、吸收、反应、传热传质等过程．为此，王江涛[7]在水平管中加入了 Kenics 静态混合器，考察了低流速下 Kenics静态混合器对液固两相流中颗粒分布的影响．但受实验条件及实验测量的影响，其流速范围较窄，实验结果也十分局限．

近年来，计算流体力学（CFD）已经成为研究液固两相流动的重要手段．目前对流化床内液固两相流动模型可以分为两类：双流体模型和Eulerian-Lagrangian模型，前者把两相均看作流体，在Euler坐标系下处理两相流，后者是把流体（液体或气体）当作连续相，而将颗粒视为离散相，在 Euler坐标系下考察流体相的运动，在 Lagrange坐标系下研究颗粒的运动．Asakura等[8]针对两相流在竖直管中颗粒碰撞进行了二维模拟，NA Patankar等人[9]采用 Eulerian-Lagrangian 方法对气-固和液-固两相流动中的颗粒流进行了数值模拟．研究颗粒体积含量较高的稠密颗粒悬浮液时，使用双流体模型更为合适一些；Eulerian-Lagrangian 模型则一般适用于湍流流动中稀疏颗粒运动的研究时采用．

本文在实验研究的基础上，通过数值模拟的方法对引入Kenics静态混合器后的水平液固循环流化床中颗粒分布特性进行研究．采用商业模拟软件 STAR-CCM+，建立水平管内液固两相流Eulerian-Lagrangian 模型，重点考察了不同液体流速下，Kenics静态混合器扭率、颗粒初始加入量对水平管内颗粒分布的影响，以期为水平液固循环流化床的研究和工程应用提供参考依据．

1 数值模拟

1.1 几何模型

在SolidWorks中生成带有Kenics静态混合器的水平液固循环流化床三维几何模型，将几何模型导入STARCCM+中，以水平管入口截面中心为原点，水平管轴线为z轴建立直角坐标系，并进行网格划分，因多面体网格能够适应任何复杂的几何形状，且占用较少的内存、拥有较高的收敛精度和更快的求解速度，故选择生成多面体网格，如图1 所示．模型为在水平管中加入扭率为 1.5 的Kenics静态混合器的多面体网格模型，网格数为 338 464 个，通过网格检查表明：面网格质量 （Face Validity） 最小值为 0.985 1（一般要求面网格在0.8 以上），可见网格质量精度较好．几何模型尺寸和流体物性及操作参数如表1 所示．

图1 网格划分示意图Fig.1 Schematic diagram ofmesh

表1 模拟主要计算参数Tab.1 Listvaluesofmain parametersused in the numericalsimulation

1.2 数学模型与数值求解方法

采用STAR-CCM+软件进行数值模拟，基于有限体积法对求解区域进行离散，建立 Eulerian-Lagrangian多相流模型，在 Euler坐标下考察液相运动，在 Lagrange 坐标系下处理颗粒相运动，速度和压力的耦合采用Simple 算法，湍流模型采用标准 k- 模型[10]，考虑相间耦合作用，两相间作用力主要考虑重力、曳力、浮力[11]，其中曳力系数采用 Gidaspow 模型[12]，动量方程采用一阶迎风差分格式进行离散．

1.3 边界条件

1）入口边界条件：入口类型设为速度入口，液固两相给定相同的入口速度，速度大小如表1所示．

2）出口边界条件：出口类型设为压力出口，出口压力为外界大气压．

3）固壁边界条件：对液相采用壁面函数法和无滑移边界条件，颗粒相不满足无滑移边界条件，颗粒相与壁面碰撞为弹性碰撞反射．

1.4 两相流雷诺数定义

本文中对液固两相流雷诺数Re做如下定义

其中：d 为水平管内径，mm；um，m，m分别为入口处两相流体的混合速度、混合密度和混合粘度，分别按照式 (2) ～式 (4) 计算．

本文中，因固体颗粒粘度极小，可忽略不计，因此混合粘度直接按照液相粘度计算．

1.5 颗粒径向浓度分布

水平管中颗粒分布问题关键在于其径向分布，为了考察固体颗粒的径向浓度分布情况，本文利用STAR-CCM+将水平管中某一轴向位置的垂直截面沿径向方向等分为5个区，分别考察各个区内颗粒浓度分布情况，如图2 所示，本文以颗粒固含率 （si）来表征颗粒浓度．

图2 水平管内径向分区图Fig.2 Sketch of subarea for the pipe in radial

2 计算结果和分析

2.1 实验验证

在与实验[7]条件相同的情况下，本文模拟了安装 Kenics 静态混合器后管内各区颗粒固含率分布情况．图3为本文模型计算结果与实验结果的对比，可以发现，安装 Kenics静态混合器后，同一雷诺数下，管内各区颗粒固含率相差较小，说明颗粒径向分布较为均匀，这一模拟结果与实验数据吻合得较好．

2.2 安装 Kenics 静态混合器前后管内颗粒分布

为了考察Kenics静态混合器对管内颗粒分布的影响，研究了液速为 1.5m/s，颗粒体积分数为 2%时，安装Kenics静态混合器（Y=1.5）前后管内颗粒分布情况，颗粒固含率数据采集位置距水平管入口处 1.5m处，研究结果如图4 ～ 图5 所示．

对比图4 与图5 可以看出，未安装 Kenics静态混合器之前，管内颗粒在流动一段距离后，因重力作用出现了下沉，导致颗粒出现分布不均匀现象；安装Kenics静态混合器之后，颗粒在螺旋流的带动下产生旋转，下沉颗粒由水平管底部向水平管上部运动，管中颗粒分布不均匀情况得到明显改善．

图3 本文模型与实验[7]结果的对比Fig.3 ComparisioN of numericalsolution in this paperwith experimentaldata[7]

图4 未安装kenics静态混合器时管内颗粒分布Fig.4 Distributionsof particlesw ithoutKenicsstaticmixer

图5 安装kenics静态混合器后管内颗粒分布Fig.5 Distributionsof particlesw ith Kenicsstaticmixer

2.3 Kenics 静态混合器扭率对颗粒固含率分布的影响

为了考察 Kenics静态混合器扭率对固体颗粒固含率分布的影响，本文研究了颗粒体积分数为 2%时，安装 Kenics 静态混合器前后以及 Kenics 静态混合器扭率分别为 1.5、2、2.5、3、3.5 时的颗粒固含率径向分布情况，研究结果如图6～ 图11所示．

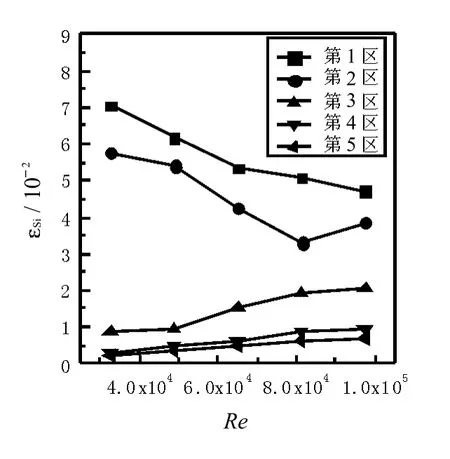
图6 未安装Kenics静态混合器时的颗粒固含率分布Fig.6 Solid holdup distributionsw ithoutKenics staticmixer

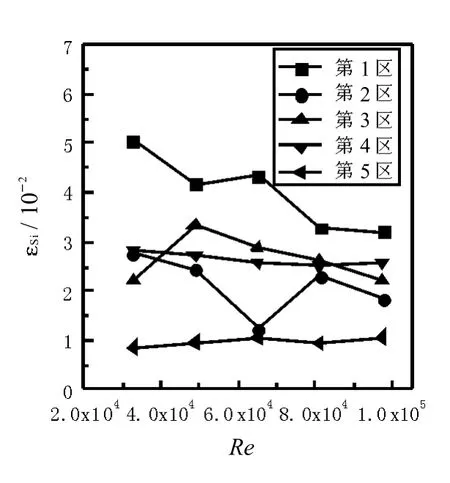
图7 扭率 Y=1.5 时的颗粒固含率分布Fig.7 Solid holdup distributionsw ith tw ist rate1.5

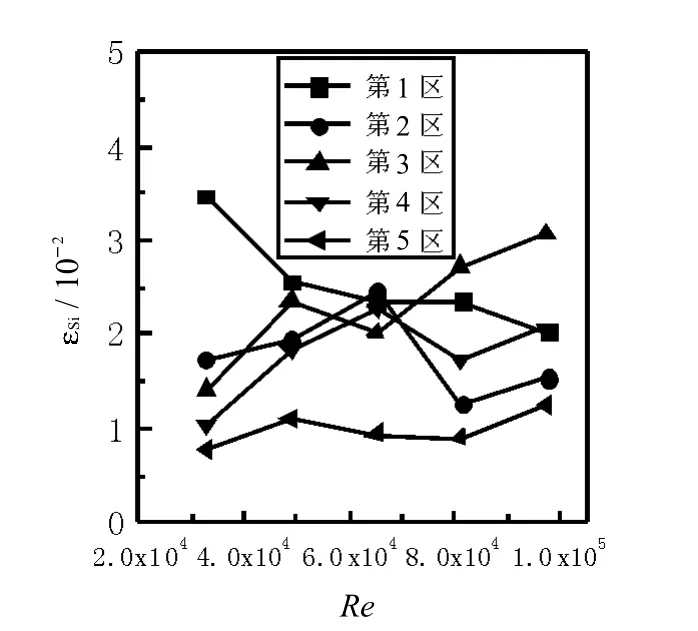
图8 扭率Y=2时的颗粒固含率分布Fig.8 Solid holdup distributionsw ith tw ist rate2

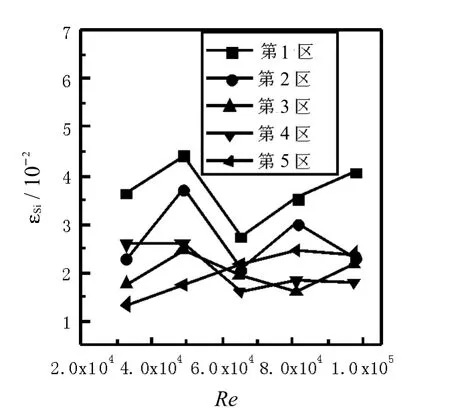
图9 扭率 Y=2.5 时的颗粒固含率分布Fig.9 Solid holdup distributionswith twist rate2.5

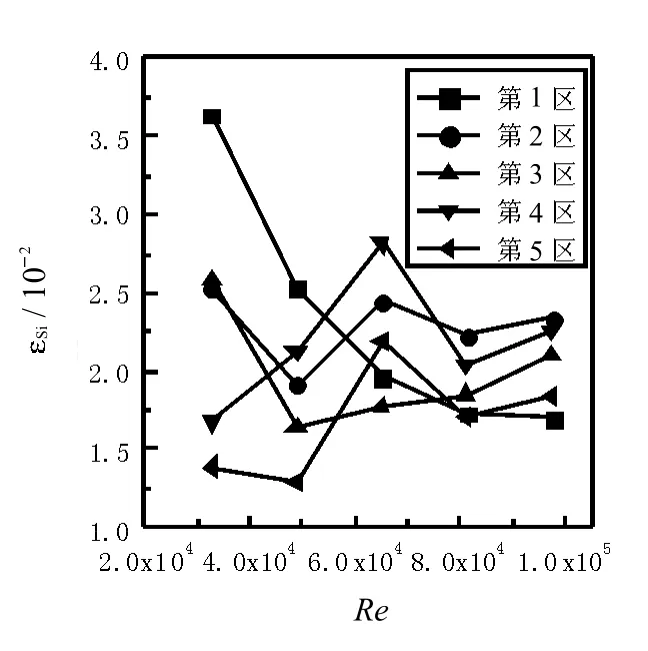
图10 扭率 Y=3时的颗粒固含率分布Fig.10 Solid holdup distributionswith tw ist rate3

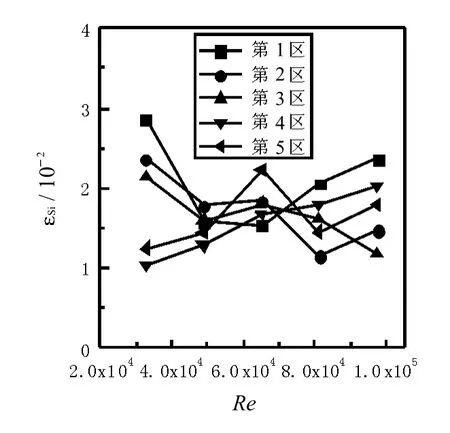
图11 扭率 Y=3.5 时的颗粒固含率分布Fig.11 Solid holdup distributionsw ith tw ist rate3.5

由图6 可以看出，未安装 Kenics静态混合器之前，同一雷诺数下，各区固含率值相差较大，1 区、2 区固含率较高，3～5区颗粒固含率较低，这主要是因为模拟时颗粒在入口处以面射源形式均匀进入管中，水平管中颗粒重力方向垂直于流体流动方向，流体的横向脉动提供的湍动能使得颗粒不至于下沉，但随着轴向距离的增加，管路阻力损失增大，能量耗损增强，液体对颗粒的拖曳力减小，紊动力不足，颗粒在重力作用下开始下沉，造成1区、2区颗粒大量堆积，3～5区颗粒大幅减小，颗粒径向分布极不均匀．但随着流速的增加，颗粒固含率径向分布不均匀情况有所改善，这主要是因为流速的增加，流体湍动程度加剧，底部颗粒在涡流带动下向上运动，颗粒分布情况得到改善，另一方面流速增大，液相对颗粒相的拖曳力增大，颗粒径向分布不均匀程度降低．液速为 2.5 ～ 3m/s时，颗粒分布情况较好．

对比图6 与图7 可知，安装 Kenics静态混合器后，颗粒径向各区固含率值相差程度减小，1 区、2 区颗粒固含率降低，3 ～ 5 区颗粒固含率呈增大趋势，颗粒分布不均匀情况得到较好改善，这主要是因为 Kenics静态混合器的螺旋结构将流体强制分割成两股，流体流向发生改变，被迫沿扭转叶片产生旋转运动，管中心为其旋转轴；同时流体自身还绕半圆形截面进行径向旋转运动，从而起到改善颗粒径向分布的作用．

对比图7 ～ 图11 可知，同时还可以看出，随着Kenics静态混合器扭率的增大，颗粒分布均匀情况越好，这是因为，扭率越大，Kenics静态混合器对液固两相流产生的旋流促进作用越强，流体被强制围绕管中心旋转，沿径向方向产生自轴心向管壁的流动，颗粒会悬浮流动增强，颗粒径向分布更加均匀．由图5～图9还可以看出，随着流速的增加，颗粒分布均匀情况也越好，这是因为流速的增加导致颗粒运动速度增大，同时加剧了液体的湍流程度，流体对颗粒的曳力和搅动增大，底部颗粒跟随流体悬浮流动，颗粒固含率分布不均匀程度降低．

2.4 颗粒体积分数对颗粒分布的影响

为了考察颗粒体积分数对固相颗粒固含率径向分布的影响，研究安装 Kenics 静态混合器后（Y=1.5），颗粒体积分数为 3%、4%、5%、6%时的颗粒固含率径向分布情况，研究结果如图12 ～ 图15 所示．

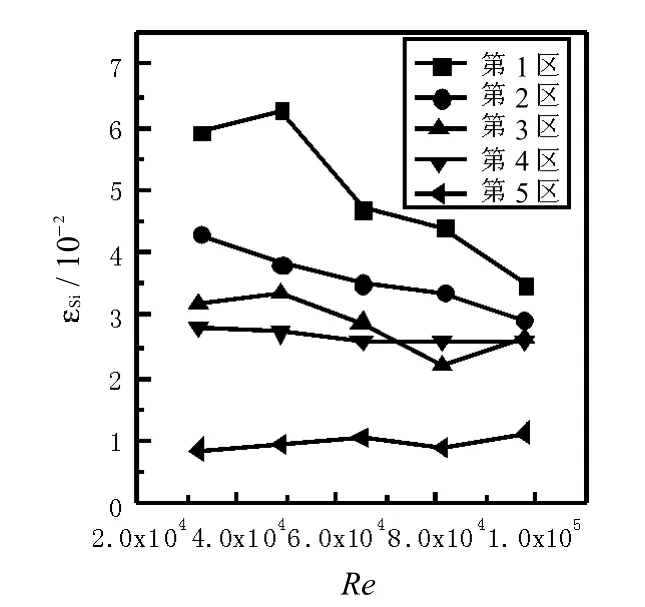
图12 颗粒体积分数为 3%时的颗粒固含率分布Fig.12 Solid holdup distributionsw ith volume fraction 3%

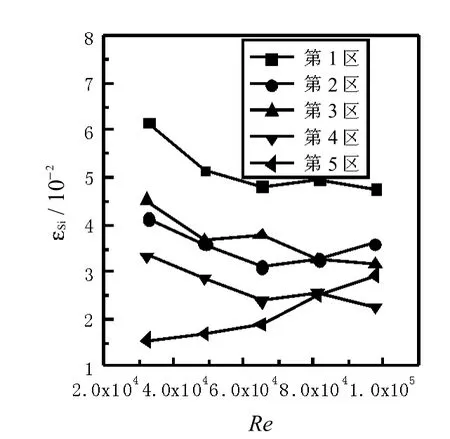
图13 颗粒体积分数为 4%时的颗粒固含率分布Fig.13 Solid holdup distributionsw ith volume fraction 4%

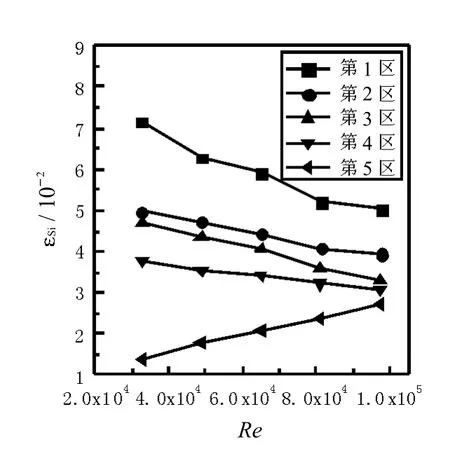
图14 颗粒体积分数为 5%时的颗粒固含率分布Fig.14 Solid holdup distributionsw ith volume fraction 5%

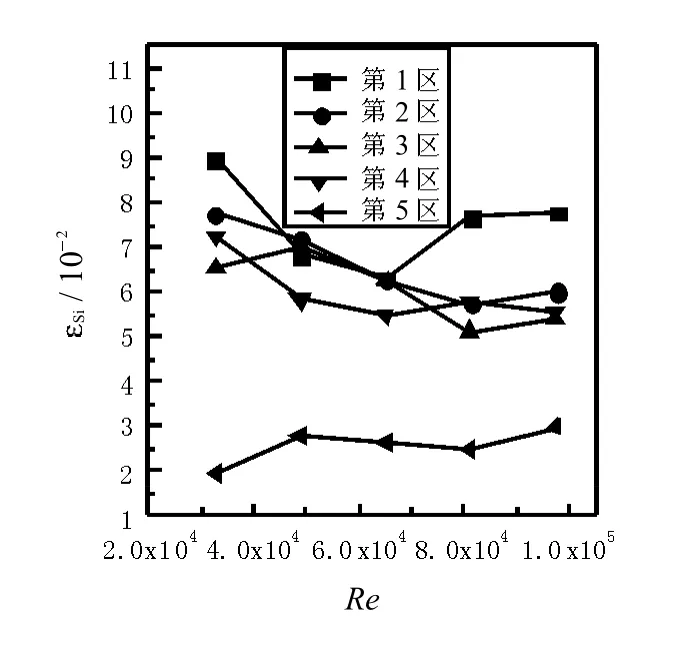
图15 颗粒体积分数为 6%时的颗粒固含率分布Fig.15 Solid holdup distributionsw ith volume fraction 6%

对比图12 ～ 图15 可知，同一雷诺数下，颗粒固含率随颗粒体积分数的增大而增大，原因是流化床内的颗粒量增大，导致参与循环的颗粒数目增大，各区固含率随之增大；另一方面颗粒体积分数增加，使管路中流体流动阻力增大，两相流湍流程度加剧，固相颗粒平均速度增大，颗粒径向不均匀分布程度降低．随着颗粒体积分数的增加，颗粒固含率分布不均匀程度呈现先降低后增大的趋势，对比图10 ～ 图13 可以看出，颗粒体积分数存在一个适宜的值，本文模拟中颗粒体积分数为4%时颗粒分布情况最好．

3 结论

1）将本文模型与实验结果进行了验证，验证了模型的可靠性．

2）未加 Kenics 静态混合器时，管内颗粒分布极不均匀，增大流速后，颗粒分布不均匀情况有所改善，雷诺数为 81 380 ～ 97 656 时，即液速为 2.5 ～ 3m/s时，颗粒分布情况较好；加入Kenics静态混合器后，颗粒固含率分布不均匀情况明显改善，且扭率越大，效果越显著．

3）Kenics 静态混合器扭率一定时，颗粒固含率分布不均匀情况呈现先减小后增大趋势，本文模拟中颗粒体积分数为4%时的分布情况较好．

[1] 贾丽云，李修伦，刘姝红，等．液固循环流化床两相流动模型 [J]．化工学报，2000，4：531-534．

[2] 姜峰，贾丽云，刘明言，等．液固循环流化床换热器中固体颗粒分布 [J]．化学工程，2004，1：17-22．

[3] 刘燕，王琦，赵斌，等．液固循环流化床换热器中颗粒分布板分布性能的实验研究 [J]．河北工业大学学报，2006，35（6）：18-24．

[4]Muller-Steinhagen，HansMalayeri，Mohammad Reza，etal．Foulingofheatexchangersnew approaches to solveanold problem[J]．HeatTransfer Engineering，2005，26（1）：1-4．

[5]Pronk P，Infante FerreiraCA，Witkamp G J．Preventionof foulingand scaling instationaryand circulating liquid-solid fluidizedbed heatexchangers：Particle impactmeasurementsand analysis[J]．International Journalof Heatand Mass Transfer，2009，52（15）：3857-3868．

[6] 姬宜朋，张沛，王丽．Kenics静态混合器的应用及研究进展 [J]．塑料科技，2005，38（ 2）：41-46．

[7] 张少峰，王江涛，刘燕．Kenics静态混合器在水平液固循环流化床中的研究 [J]．化学工程，2012，40（6）：44-46．

[8]Bolio EJ，Yasuna JA，Sinclair JL．Dilute turbulentgas-solid flow in riserswithparticle-particle interactions[J]．AICHEJournal，1995，41（6）：1375-1388．

[9]Patankar N A，Joseph D．Modeling and numericalsimulation of particulate flowsby the Eulerian-Lagrangian approach[J]．International Journalof Multiphase Flow，2001，27（10）：1659-1684．

[10]Liu D Y．Fluid dynamicsof two-phase systems[M]．Beijing：Higher Education Press，1993．

[11]Gidaspow D．Multiphase flow and fluidization：continuum and kinetic theory descriptions[M]．USA：Academic Press，1994．

[12] 陶文铨．数值传热学 [M]．西安：西安交通大学出版社，2001．

[责任编辑 田 丰]

Numericalsimulation ofparticledistribution in liquid-solid horizontalcirculating fluidized bedw ith Kenicsstaticmixer

LIU Yan1，ZHANG Li-mei2，ZHANG Shao-feng1，DU Ya-wei1
(1.SchoolofMarine Scienceand Engineering,HebeiUniversity of Technology,Tianjin 300130,China;2.Schoolof Chem icalEngineering,HebeiUniversity of Technology,Tianjin 300130,China)

Particle distribution of liquid-solid two-phase flow for low concentration in horizontalpipew ith Kenics static m ixerwasnumerically simulated by using the Eulerian-Lagrangianmodelin software STAR-CCM+.Theeffectsof liquid velocity,tw ist rateof Kenics staticm ixerand particle volume fraction on the particle distribution in horizontalpipewere discussed.Results indicate that the radialnon-uniform distribution of particles in pipe ispromoted effectively by Kenics staticm ixer.Meanwhile,w ith the increase of Kenics tw ist rate,theeffecthasbecomemore obvious.The increase of the liquid velocity hasimproved the radialnon-uniform distribution ofparticles.Thesituation also applies for the increase of particle volume fraction.Dependability of the selectedmodelswasvalidated comparedw ith the experimentaldata reported in the literature.

liquid-solid circulating fluidized bed;Kenicsstaticmixer;particle distribution;numericalsimulation;horizontal tube

1007-2373(2014)05-0049-06

TQ051

A

10.14081/j.cnki.hgdxb.2014.05.009

2014-05-08

河北省科技支撑项目（12276711D）

刘燕（1970-），女（蒙古族），副教授，博士，E-mail：julia_liuyan@hotmail.com ．