基于有序聚类法的大中修路段划分技术研究

马士宾，虞秋富，张 静，袁文瑞

（河北工业大学 土木工程学院，天津 300401）

基于有序聚类法的大中修路段划分技术研究

马士宾，虞秋富，张 静，袁文瑞

（河北工业大学 土木工程学院，天津 300401）

利用有序样本的聚类划分方法，将待修路段的检测数据看作是一个有序检测样本，应用 Fisher算法中损失度函数的概念，将路面评价指标按照一定的权重综合加权计算损失度函数，以损失度函数达到极小值为目标进行大中修路段长度划分．列举实例说明该算法的计算步骤，进一步证实该方法的可操作性．

有序聚类；路面大中修；权重指标 ；Fisher算法；路段划分

我国《公路技术状况评定标准》（JTGH20-2007） 规定路面性能评价基本单元为 1 km ，为了方便，在路面进行大中修养护设计时也通常是采用整公里桩号作为分界点[1]，即以里程桩为分界进行养护划分路段．由于等长度路段划分方法具有操作简单和管理方便的优点而被广泛应用，但这种方法主观的认为路段在整公里桩号（1 km）范围内路段具有相同或相近的属性，这显然与路面实际工作状态不同．因此，研究如何更加合理划分路段，科学进行养护路段划分十分必要．国内目前许多专家学者已经开始从事这方面的研究．华南理工大学的农家萍、张肖宁[2]尝试将灰聚类方法应用于养护路段划分中，将待养护的沥青路面看作一个灰色系统，建立聚类对象的三角白化权函数，计算各对象的综合聚类系数，得出路面的聚类向量，由此完成路段划分．长沙理工大学的王佳、胡列格[3]应用有序样本聚类分析进行路段划分．对于一条公路的大中修来说，它不同于普通的养护工作，大中修路段的长度可以达到几公里甚至十几公里．需进行大中修的公路不可能恰恰在整公里处损坏模式，破坏程度刚好发生变化．这就必须依据路段损坏程度、破坏模式对公路进行路段划分，使得同一种大修方案具有相似属性（程度相同和破损类型）．

结合以上问题，本文基于有序聚类分析与Fisher算法结合，按照路面结构评价指标相似程度不同来进行大中修路段划分．

1 有序聚类分析法

在公路实际检测过程中，检测样本数据不同于其他样本数据，为了保持路的连续性，检测样本需要在路线前进方向上保持连续性，数据顺序不能打乱．而且进行大修设计时，路线长度方向一定范围内必须采用相同的大中修方案，以保证连续施工．设代表 n 个路面检测样本，对其进行划分时要求每一类内数据成员必须是连续的，其数据形式为：，其中 i＜ j ，这种问题的分类方法称为有序样本聚类法，又称为最优分割法[4]．

2 有序聚类法方法分析原理及步骤

2.1 类直径的定义

用 D i,j 表示该类的直径，应用欧几里得距离定义直径计算方法

2.2 定义损失函数

bn,c表示将 n 个有序路面检测样本数据分为 c 个养护路段的一种划分方法[6]，即，其中，，定义这种路段划分方法的损失函数为

其中 ic+1=n+1 ．当检测数据 n 和路段划分数量 c 固定时，L bn,c取值越小，说明 c 路段的离差平方总和取值越小，表示大中修路段内部路面结构特性越接近，大中修路段划分越合理．

2.3 L bn,c的递推公式

Fisher算法[7]核心的部分是利用 2 个递推公式

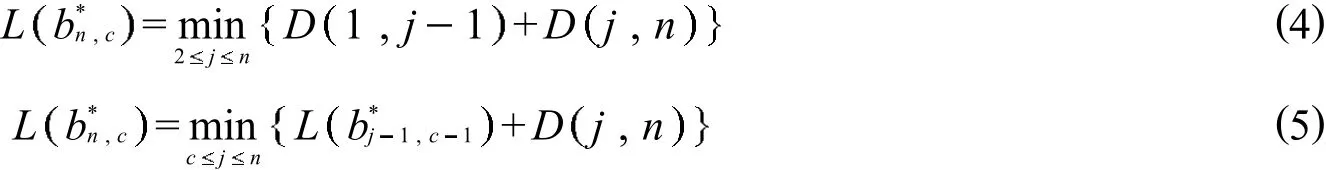
式 (4) 是 c=2 的情况，即递归出口，这时 b1,2为由式(3)得

2.4 求最优解

假设 c 1＜c＜n 已知，即路段划分数目已知，当损失函数式 (3)达到极小，可求得最优分类，求法如下：

首先找第 1 个分点，使公式 (5) 达到极小，即

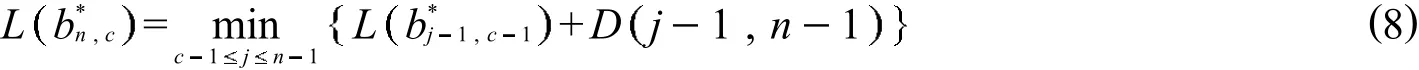
3 实例分析

公路进行大中修设计时，要将路面破坏状况相似而且位置相邻的路段划分到同一区域进行大中修设计，如果两个路段破坏状况相似，但是两个路段相距很远，不能在一起连续施工，同样不可以划分在同一个区域．这就使公路大中修路段划分时有了顺序要求．对于一条公路，将每一个检测点看成是检测样本点，这些检测样本点则按照里程桩号排列成了一个有序检测样本．根据路面评价指标体系，每个检测样本点具有 PCI，RQI，RDI，SRI 4 项评价指标，由它们共同确定路面的 综 合 评 价 指 数RDI+SRI× SRI．权重指标如表1．

如果在路段划分时将各个指标综合后，按照路面的综合评价指数 PQI进行划分，同样会出现划分结果奇异的情况，即2个路段的各个评价指标不相近或者相差很大，但是综合之后的 PQI却相近．为了避免这种情况出现，本文将每个检测样本点看成由四项指标构成的四维向量．

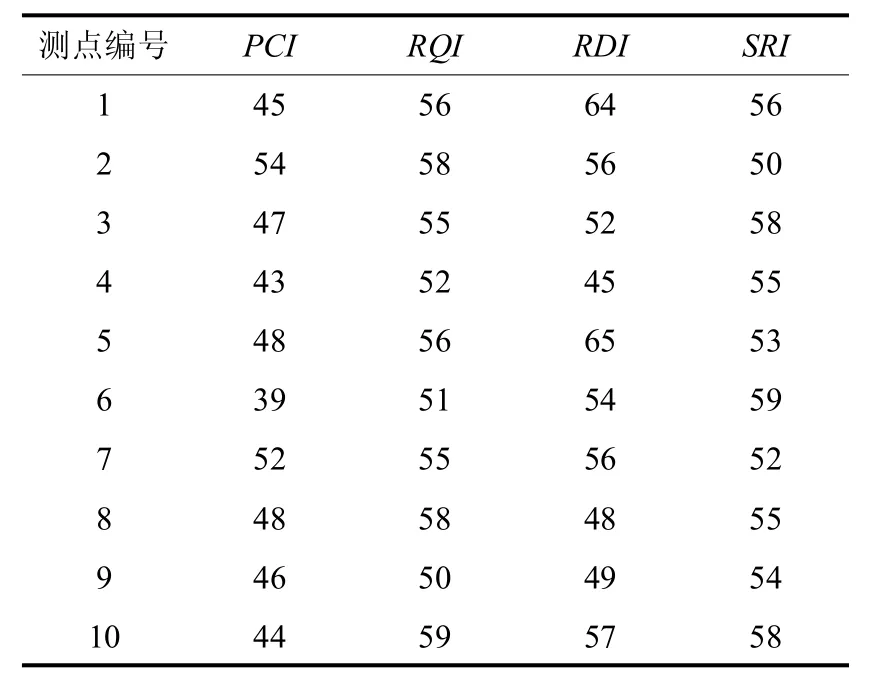
沧州某条公路的部分检测结果如表2所示．

3.1 计算直径

表1 PQI分项指标权重

Tab.1 Sub-index weights PQI

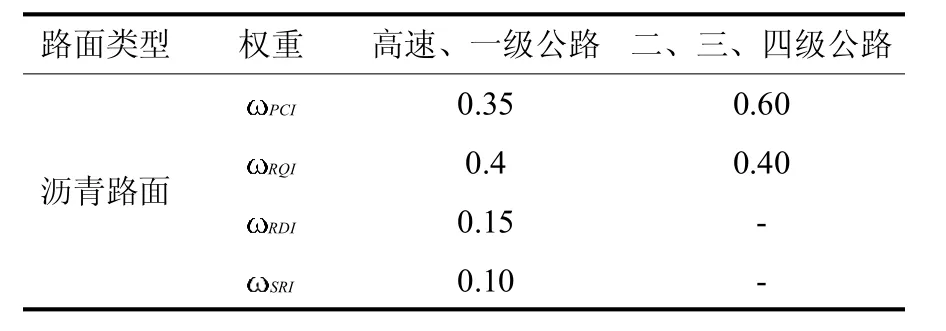
表2 公路的部分检测结果Tab.2 Test resultsof road

首先计算 15 个检测样本一切可能的检测样本段直径，由 (1) 得每一个检测样本中一个维度的直径，按照路面综合评价指数的分项权重加权得到式 (9)

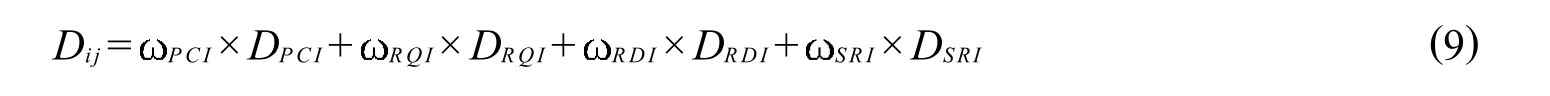
测点编号 P C I R Q I R D I S R I 1 4 5 5 6 6 4 5 6 2 5 4 5 8 5 6 5 0 3 4 7 5 5 5 2 5 8 4 4 3 5 2 4 5 5 5 5 4 8 5 6 6 5 5 3 6 3 9 5 1 5 4 5 9 7 5 2 5 5 5 6 5 2 8 4 8 5 8 4 8 5 5 9 4 6 5 0 4 9 5 4 1 0 4 4 5 9 5 7 5 8

计算结果列于表3．

根据专家鉴定，将大修路段分为3段，即 c=3．分段过程如下，首先将所有检测样本看成一类，然后将这类划分 c=2，按照式4计算最小损失函数．例如，当检测样本数为2时，划分2段时显然损失函数为0，检测样本数为 3 时，划分两段的方法有 2 种，即｛1｝、｛2，3｝ 和｛1，2｝、｛3｝．损失度函数计算式

j=2 时取极小值，记为 7.4(2)．同样的，当检测样本数为 4，5，…，10 时，分成 2 个区段均按照式 (4)计算．计算结果见表3．

c=2 划分完毕后继续划分 c=3 ，按照式 (5) 计算，n=3 时显然损失函数为 0，检测样本数为 4 时计算式

j=3 时取极小值，记为 4.4(3) 同样的，当检测样本数为 4，5，…，10 时，分成 3 个区段均按照式 (5)计算．本文将该段划分为 4 部分，计算结果均填入表4．

该路段有序检测样本划分的4个聚类组成方式：1） 首先找出最小损失度函数对应数值 73.8(7) ，则最小损失度函数对应数值 30.2(5)，则最小损失度函 数对 应 数 值，则

通过以上实例可以看出，应用聚类划分大修路段可以将路面结构指标相近的路段划分到同一区段，避免了经验划分方法中决策人员主观意识造成的误差，为公路养护技术科学化决策提供依据．

表3 检测样本各个维度加权后的直径Tab.3 Samples tested each dimensionweighted diameter

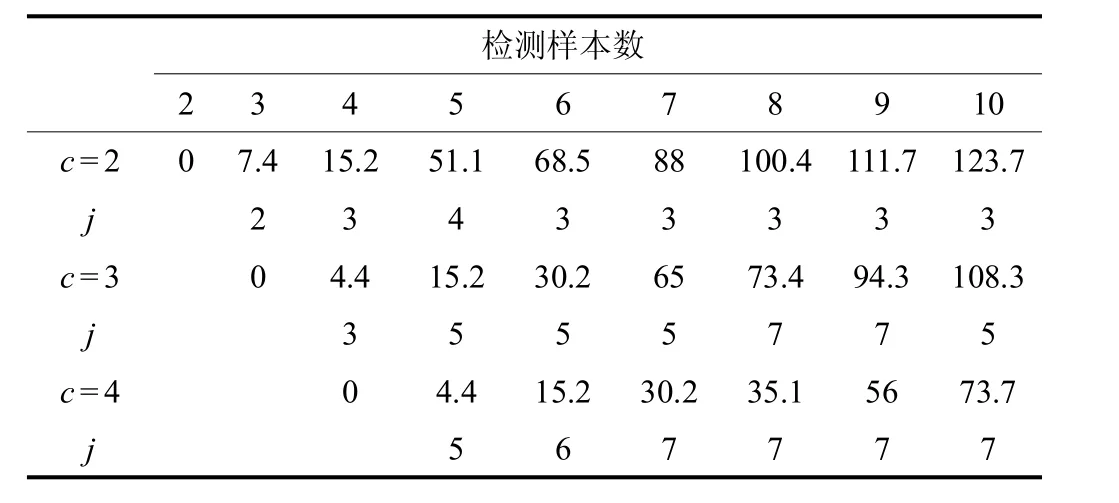
表4 损失度函数计算结果Tab.4 Calculation resultsof loss function

4 结论

本文将有序聚类原理应用于路面大中修路段长度划分，具有以下优点：

1）提出了一种大中修路段划分新方法，并且将路面评价中的权重思想融入划分过程，给出了大中修路段长度划分的理论依据．

2）避免了由于路面大中修路段长度划分不合理造成的路面材料浪费或者大修之后某些路段强度不足．

3）通过实例可以看出，该方法可以准确的将所需长度划分的路段按照性能相似程度划分成想要的合理段数，而且划分结果准确．不会出现模棱两可的区域．

[1] 周焯华，陈文南，张宗益．聚类分析在证券投资中的应用 [J]．重庆大学学报：自然科学版，2002，25（7）：122-126．

[2] 农家萍，张肖宁．模糊聚类分析在沥青路面养护路段划分中的应用 [J]．中外公路，2006，26（3）：119-122．

[3] 王佳，胡列格．养护路段的有序聚类划分 [J]．系统工程，2008，26（11）：71-74．

[4] 刘晓波，黄其柏．基于动态核聚类分析的水轮机组故障模式识别 [J]．华中科技大学学报：自然科学版，2005，33（9）：47-49，52．

[5] 曾峰，张肖宁，李智．应用聚类分析法确定沥青路面预防性养护方案 [J]．华南理工大学学报：自然科学版，2008，36（6）：67-71．

[6] 陈英杰．沥青路面养护路段划分方法研究 [J]．科学技术与工程，2010，10（22）：5584-5587．

[7] 徐显海．Fisher有序聚类法及其在炉管温度异常时段提取中的应用 [J]．广西电力，2005（5）：15-17．

[责任编辑 杨 屹]

Technical research on pavementmaintenance division based on ordered sample clustering

MA Shi-bin，YU Qiu-fu，ZHANG Jing，YUANWen-rui
(Schoolof CivilEngineering,HebeiUniversity of Technology,Tianjin 300401,China)

Themethod ofordered sample clustering isapplied to calculate the length of pavementmaintenance.With the detection dataof pavementundermaintenance regarded asan ordered sample in calculating the loss functionw ith the Fishermethod,onedivisionmethod forpavementmaintenance isgiven outafterweighing all the loss functions for the pavementquality indexes.Oneexample isgiven to show theprocessof themethod.The resulthasproved thismethod is feasible.

ordered clustering;pavementmaintenance;weightindex;Fisher;divisionmethod

1007-2373(2014)05-0106-04

U418

A

10.14081/j.cnki.hgdxb.2014.05.021

2013-12-16

河北省高等学校科学技术研究项目（ZD2014099）

马士宾（1974-），男（汉族），副教授，博士．