关于图Gp，q，sa，b，c的一个重要结论*

李 丹，苏 宇，张力丹，王国平

关于图Gp，q，sa，b，c的一个重要结论*

李 丹，苏 宇，张力丹，王国平

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

让Gp，q，sa，b，c表示阶为n的由三个lollipop图通过一个公共点连接的图.首先确定了φ（Pn，－2）的值，其次得到了2是图Gp，q，sa，b，c的特征值的充要条件.

谱；路；圈

1 基础知识

在这篇文章中，我们只考虑简单无向图.设G是阶为n的图，A（G）表示其邻接矩阵.因为A（G）是实对称矩阵，所以它的所有特征值均为实数.我们分别用φ（G）＝φ（G，λ）表示图G的A－特征多项式，SpecA（G）＝｛λ1（G），λ2（G），…，λn（G）｝（非增序列）表示图G的A－谱.通常，用Cn和Pn分别表示n阶圈和路.lollipop图是将圈Cp连接在路Pn－p＋1的一个悬挂点上得到的图，用Hp，n－p表示.θ－图是由三条具有公共端点的内部两两不交的路Pa，Pb，Pc得到的图，用θa，b，c（a≤b≤c）表示.Dumbbell图是在路Pc＋3（c≥－1）的两个端点连接两个内部不交的圈Ca，Cb，用Da，b，c表示.文献［1］和［2］刻画了lollipop图谱；［3］刻画了θ－图谱；［4］刻画了Dumbbell－图谱.设Gp，q，sa，b，c表示具有公共端点的三个内部两两不交的lollipop图（见图1）.

图1 Gp，q，sa，b，c的结构

本文首先证明了φ（Pn，－2）的值；其次确定了2∈ Spec（G）当且仅当（a，b，c）∈Ω＝｛（2，3，6），（2，4，4），（3，3，3），（0，0，c）（c≥0）｝.

2 主要结论

本节中，我们将给出主要结论.

引理2.1［5］设G是一个简单图.～Cv（～Ce）表示图G中包含点v（边e＝uv）的所有圈的集合.那么：

（2）φ（G，λ）＝φ（G－e，λ）－φ（G－u－v，λ）－

定理2.2 设Pn是n阶路.那么：

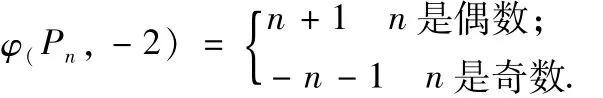
证明由引理2.1，有

如果λ＝－2，那么

因为φ（Pn－1，－2）＝－2φ（Pn－2，－2）－φ（Pn－3，－2），进而可以得到φ（Pn，－2）＝3φ（Pn－2，－2）＋2φ（Pn－3，－2）.

按照这种步骤很容易有：当n为偶数时，φ（Pn，－2）＝（n－1）φ（P2，－2）＋（n－2）φ（P1，－2）＝n＋1；当n为奇数时，φ（Pn，－2）＝－（（n－1）φ（P2，－2）＋（n－2）φ（P1，－2）＝n＋1）＝－n－1.

引理2.3（交错定理）［6］设A是n×n的对称矩阵，其特征值为λ1，λ2，…，λn.B是A的一个m×m主子式，其特征值为λ*1，λ*2，…，λ*m.那么λi≥λ*i≥λn－m＋i（i＝1，2，…，m）.

引理2.4［7］Pn，Ta，b，c，θa，b，c和Hg，p分别表示路，T－型树，θ－图和lollipop图.那么：

（1）φ（Pn，2）＝n＋1；φ（Ta，b，c，2）＝a＋b＋c＋2－abc；φ（Qa，b，c，2）＝4a＋4b＋4c－4ac－2bc－2ab＋abc，其中Qa，b，c是恰有两个三度点的树；

（2）φ（θa，b，c，2）＝ijk－（ij＋ik＋jk）－3（j＋i＋k）－5；

（3）φ（Hg，p，2）＝－gp；

（4）φ（Da，b，c，2）＝abc，并且2∈Spec（Da，b，c）当且仅当c＝0，2是单根.

定理2.5 设3≤p≤q≤s，0≤a≤b≤c，那么2∈Spec（Gp，q，sa，b，c）当且仅当（a，b，c）∈Ω＝｛（2，3，6），（2，4，4），（3，3，3），（0，0，c）（c≥0）｝.

此外，当（a，b，c）∈Ω／（0，0，0）时，2是单根；当（a，b，c）＝（0，0，0）时，2是二重根.

证明由引理2.1可以得到φ（Gp，q，sa，b，c）＝φ（Hp，a）φ（Dq，s，b＋c）－φ（Hp，a－1）φ（Hq，b）φ（Hs，c），

进而通过引理2.4又有

因此2∈Spec（Gp，q，sa，b，c）当且仅当abc－ab－ac－bc＝0.解这个等式可以得到

这隐含着c是关于a和b严格递增的.所以当c≥b≥a≥4时，c在b＝a＝4是取得最大值，且由（2）可以直接得到，但这和c≥4是矛盾的.所以2∉Spec（Gp，q，sa，b，c）.

接下来，只需要考虑0≤a≤3的情况.

现在证明第二部分.设u1，u2，u3和u4是Gp，q，sa，b，c中的三度点.接下来我们考虑两种情况.

情形1（a，b，c）∈Ω／（0，0，0）

如果（a，b，c）＝｛（2，3，6），（2，4，4），（3，3，3）｝，由引理

当（a，b，c）＝（0，0，c）（c≠0）时，分两步观察.

（2）λ1λ1（G″）＞λ2（G″）＞2，λ3（G″）＜2，所以

因此当（a，b，c）∈Ω／（0，0，0）时，2是单根.

情形2（a，b，c）＝（0，0，0）

［1］Boulet R，Jouve B.The lollipop graph is determined by its spectrum［J］.The Electronic Journal of Combinatorics，2008.

［2］HaemersW H，Liu X，Zhang Y.Spectral characterizations of lollipop graphs［J］.Linear Algebra and Its Applications，2008，（11）：2415－2423.

［3］Ramezani F，Broojerdian N，Tayfeh－Rezaie B.A note on the spectral characterizations ofθgraphs［J］.Linear Algebra and Its Applications，2009，（5）：626－632.

［4］Wang J，Huang Q，Belardo F，et al.A note on the spectral characterizations of dumbbell graphs［J］.Linear Algebra and Its Applications，2009，（10）：1707－1714.

［5］Cvetkovic D M，Doob M，Sachs H.Spectra of Graphs：Theory and Application［M］.New York：Academic Press，1980.

［6］Van Dam E R，HaemersW H.Which graphs are determined by their spectrum？［J］.Linear Algebra and Its Applications，2003，373：241－272.

［7］Ghareghani N，OmidiGR，Tayfeh－Rezaie B.Spectral characterization of graphs with index atmost［J］.Linear Algebra and Its Applications，2007，（2）：483－489.

A M ain Result on the Graph G

LIDan，SU Yu，ZHANG Lidan，WANG Guoping
（School of Mathematical Sciences，Xinjiang Normal University，Urumqi Xinjiang 830054，China）

Let Gdenote the graph on n vertices obtained by taking three lollipop graphswith justa vertex in common.In this paper，we first prove thatφ（Pn，－2）＝n＋1 if n is even andφ（Pn，－2）＝－n－1 if n is odd；we then determine2∈Spec（G）if and only if（a，b，c）∈Ω＝｛（2，3，6），（2，4，4），（3，3，3），（0，0，c）（c≥0）｝.

spectrum；path；cycle

O157.5

A

1008－4681（2014）02－0005－02

（责任编校：晴川）

2013－08－21

李丹（1988－），女，新疆哈密人，新疆师范大学数学科学学院硕士生.研究方向：图论与组合数学.