基于收缩估计法的广义Pareto分布参数的估计*

陈兆仁，刘婉贞

基于收缩估计法的广义Pareto分布参数的估计*

陈兆仁1，刘婉贞2

（1.湖南师范大学工程与设计学院，湖南长沙410081；2.长沙职业技术学院，湖南长沙410010）

由于广义Pareto分布在金融和保险等领域的广泛应用，对于该分布的统计推断成为研究的热点.将在参数的先验分布为倒伽玛分布条件下研究广义Pareto分布参数的Bayes估计问题，并在平方误差和LINEX损失函数下，导出了参数的Bayes估计和Bayes收缩估计.文末给出了Monte Carlo数值模拟试验和结论.

广义Pareto分布；Bayes估计；收缩估计；损失函数

广义Pareto分布（GPD）自Piekands［1］提出以来被广泛地应用于金融、保险、灾害预测等诸多领域.关于其统计推断研究引起了很多学者的关注.Rasmussen［2］提出了GPD参数估计的广义概率加权法；赵旭等［3］针对截尾样本提出了GPD参数估计的广义有偏概率加权矩法；Ashkar等［4］对以前学者提出的最大似然估计法、矩估计法、概率加权矩估计法以及广义概率加权矩估计法进行回顾总结，发现这些方法在形状参数为正值时，广义Pareto分布参数常有一个上界值.特别是在处理洪水数据时，这种情况常出现，以往的方法得到的估计值常高出这个上限值，于是其利用Monte Carlo数值模拟对几类估计方法进行比较，进而提出了一些建议.在工程实践中，很多学者意识到将有关未知参数的先验知识融入到参数的估计中将能改善原有的估计，如收缩估计.Thompson［5］提出了估计总体均值参数的如下收缩估计：

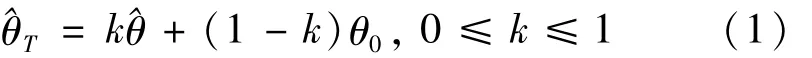
这里θ0为参数先验值，＾θT称为Thompson型估计.关于收缩估计的更多的研究参见文献［6－8］.基于收缩技术研究GPD参数估计问题还未见有文献讨论，因此本文讨论GPD参数的Bayes收缩估计问题.由于在实际中用的最多的是两参数GPD分布：

其中β＞0.且当ξ≥0时，x∈［0，∞）；当ξ＜0时，x∈［0，－］.于是本文接下来的研究中只考虑参数ξ＜0的情况.令θ＝－ξ，σ＝，则此时两参数GPD分布变为：

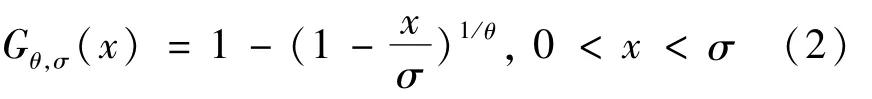
其中θ，σ＞0为参数.

本文将在σ已知的情况下，在参数θ的先验分布为倒伽玛分布的条件下，研究在平方误差损失、LINEX损失函数下广义Pareto分布参数的Bayes收缩估计问题.

1 预备知识

引理1 设X1，X2，…，Xn为来自广义Pareto分布（2）的简单随机样本，记X＝（X1，X2，…，Xn），t的样本观测值，设参数θ的先验分布为逆伽玛分布IΓ（α，β），相应的概率密度函数为：

（iii）θ｜X～IΓ（n＋α，β＋T）.

证由（1）得到，在给定x＝（x1，x2，…，xn）下，参数θ的似然函数为：

由（3）、（4）及Bayes定理，参数θ的后验概率密度函数为：

从而θ的后验分布为倒伽玛分布IΓ（n＋α，t＋β）.即后验概率密度函数为：

引理得证.

2 Bayes估计和Bayes收缩估计

在这一部分，我们总设X＝（X1，X2，…，Xn）为来自分布（2）的容量为n的简单随机样本，并设T为研究参数的Bayes估计问题，下面将在平方误差损失函数和LINEX损失函数下研究参数的Bayes和Bayes收缩估计问题.

2.1平方误差损失函数下的Bayes估计和Bayes收缩估计

在平方误差损失函数L1（＾θ，θ）＝（＾θ－θ）2下，参数θ的Bayes估计为其后验期望，即有：

现假设根据已有的工程经验已知参数θ的先验估计值为θ0，采用文献［8］的方法确定超参数α，β值：令E（＾θB）＝θ0，由引理1得β＝（α－1）θ0，将其代入（7）有：

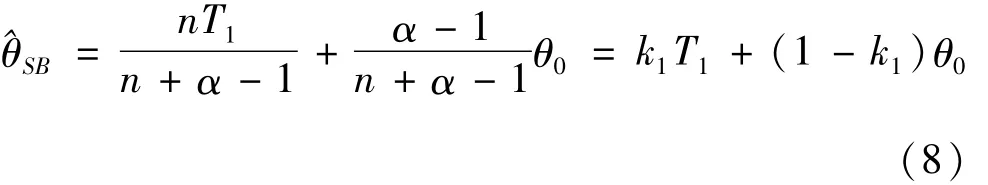
这恰好具有（1）的形式，我们把通过这种方法得到的估计称为Bayes收缩估计.

2.2LINEX损失函数下的Bayes估计和Bayes收缩估计

本文采用的LINEX损失函数是由文献［9］首先提出的，其函数表示形式为：

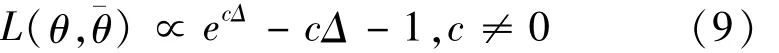
易证在LINEX损失函数下参数θ的Bayes估计由下式给出：

由于

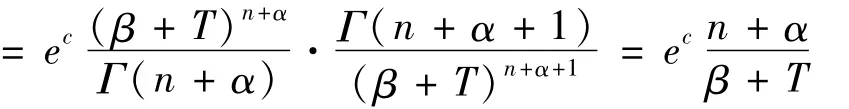
则由（9）解得在LINEX损失函数下，参数θ的Bayes估计为：

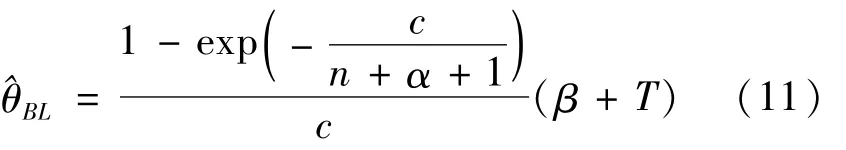
下面采用类似的方法确定先验分布中的超参数α，β值：

令E（＾θBL）＝θ0，由引理1得

将β值（12）代入（11）中，有：这里k2＝nw.这也具有（1）的形式，也称为Bayes收缩估计.

3 数值模拟例子

利用Monte Carlo数值模拟生成容量为n＝20的来自广义Pareto分布（2）的简单随机样本，其中σ＝1.0，θ＝1.0.重复试验N＝5000次，将估计的平均值即作为参数θ的估计值，利用均方误差

来考察估计的优良性，其中＾θi为第i次试验的参数θ的估计值.参数的最大似然估计（MLE）、Bayes估计以及Bayes收缩估计值见表1.

表1 参数的MLE、Bayes及Bayes收缩估计值和相应的均方误差（c＝1）

从表1及大量的数值模拟试验我们得到如下结论：

（1）当Bayes估计受两个超参数的影响，而Bayes收缩估计由于不但利用了参数先验值θ0，而且仅受一个超参数的影响时，若实际中我们得到的参数先验值θ0较接近真值，Bayes收缩估计相对Bayes估计而言稳健性更好，因而推荐使用Bayes收缩估计方法对参数进行估计；

（2）当样本容量n较大时，各类估计均较接近真实值.

本文在假定寿命分布服从广义Pareto分布（2）情况下，取得了未知参数的最大似然估计，并在平方误差以及LINEX损失函数下得到了参数的Bayes估计和Bayes收缩估计.本文所提出的收缩估计法可以推广到诸如指数分布、Weibull分布、Burr Type XII分布等寿命分布模型.

［1］Pickands J.Statistical inference using extreme order statistics［J］. Annals of Statistics，1975，（1）：119－131.

［2］Rasmussen P F.Generalized probability weighted moments：Application to the generalized pareto distribution［J］.Water Resources Research，2001，（6）：1745－1751.

［3］赵旭，程维虎，李婧兰.广义Pareto分布的广义有偏概率加权矩估计方法［J］.应用数学学报，2012，（2）：321－329.

［4］Ashkar F，Tatsambon N C.Revisiting some estimation methods for the generalized pareto distribution［J］.Journal of Hydrology，2007，（6）：136－143.

［5］Thompson JR.Some shrinkage techniques for estimating the mean［J］.Journal of American Statistical Association，1968，（321）：113－122.

［6］Qabaha M.Ordinary and Bayesian shrinkage estimation［J］.An－Najah University Journal for Research，2007，（1）：101－116.

［7］Prakash G，Singh D C.A Bayesian shrinkage approach in weibull type－II censored data using prior point information［J］.Revstat－Statistical Journal，2009，（2）：171－187.

［8］Prakash G，Singh D C.Bayesian shrinkage estimation in a class of life testing distribution［J］.Data Science Journal，2010，8：243－258.

［9］Varian H R.A Bayesian approach to real estate assessment［A］. Studies in Bayesian Econometrics and Statistics in Honor of Leonard JSavage［C］.Amsterdam，1975.

Estimation of Parameter of Generalized Pareto Distribution Based on Shrinkage Technique

CHEN Zhaoren1，LIUWanzhen2
（1.College of Engineering and Design，Hunan Normal University，Changsha Hunan 410081，China；2.Changsha Vocational＆Technology College，Changsha Hunan 410010，China）

The generalized Pareto distribution is extensively used in the field of finance，insurance，etc.The statistical inference for the distribution has been a hot spotof research.The aim of this paper is to study the Bayes estimation of the parameter of the parameter of the generalized Parato distribution based on the parameter prior is inverse Gamma distribution.Under squared error loss and LINEX functions，Bayes and shrinkage estimators are obtained，and Monte Carlo simulation experiment and conclusion is given at last.

generalized Pareto distribution；Bayes estimation；shrinkage estimator；loss function

O212.8

A

1008－4681（2014）02－0001－04

（责任编校：晴川）

2013－12－18

陈兆仁（1965－），男，湖南长沙人，湖南师范大学工程与设计学院副教授.研究方向：Bayes统计、模糊决策.