一类高阶自共轭微分算子谱的定量分析*
2014-07-20钱志祥
钱志祥
一类高阶自共轭微分算子谱的定量分析*
钱志祥
(肇庆科技职业技术学院基础教学部,广东肇庆526100)
定量研究了一类高阶自共轭微分算子的谱,得到了这类算子的本质谱充满了正实轴,而在负半轴上只有离散谱.
微分表达式;对称微分算子;自共轭微分算子;离散谱;本质谱;谱分析
1 预备知识
微分算子理论是解决量子力学问题的基本工具,量子力学的迅速发展也极大地推动了微分算子理论的研究,在核物理学、电子学,以及许多其他数学分支中,微分算子理论也起到了重要的作用.自共轭微分算子谱理论是微分算子理论的重要内容,它已经经历了一个多世纪,其谱理论成果十分丰富,尤其在自共轭微分算子谱的定性分析方面取得了突破性的进展[1],但是在自共轭微分算子谱的定量分析方面,结论却寥寥无几.自共轭微分算子谱的定性、定量研究是微分算子理论的重要组成部分,一个自共轭微分算子的谱不仅与其系数有关,还与它的定义域和自伴边条件有关,因为自共轭微分算子的系数、定义域和边值条件的形式是复杂多样的,所以这就给自共轭算子谱的定量研究带来了很大的难度,本文目的是对2n阶自共轭微分算子在其系数、定义域和边值条件满足特定条件时的谱进行定量分析.
考虑2n阶对称微分表达式:
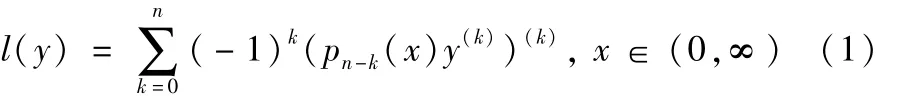
(I)其系数满足:
(II)其定义域D(T)和边值条件满足:
1)y(2n-1)在[0,∞)上存在且在[0,∞)的每个稠密子集上绝对连续;
2)l(y)∈L2[0,∞);
定义1.1[2]定义算子TM:TMy=l(y),D(TM)={y∈L2(a,b),y(k)在(a,b)上绝对连续,0≤k≤n-1,l(y)∈L2(a,b)},称算子TM为由微分算式l(y)生成的最大算子.
定义算子T′0:T′0y=l(y),D(T′0)={y∈D(TM),y在(a,b)内具有紧支柱},T′0的闭包记为T0,称算子T0为由微分算式l(y)生成的最小算子.
定义1.2[3]对于定义在Hilbert空间X上的闭稠定线性算子T,若对任意λ∈C,存在常数K=K(λ)>0,使得对所有x∈D(T),(A-λI)x≥K x,则称数λ为算子T的正则型点;T的所有正则型点的全体称为算子的正则型域,记为Π(T),即Π(T)={λ∈C|∃K(λ)>0,使得A-λI)x≥K x,∀x∈D(T)}.
定义1.3[3]集合C\Π(T)称为算子T的谱核,记为σk(T)或kσ,即σk(T)=C\Π(T).
定义1.4[4]T是Hilbert空间H上的自共轭算子,σ(T)中的全体聚点和无穷维的孤立的特征值点称为T的本质谱,记为σe(T).本质谱在谱集中的补集称为T的离散谱,记为σd(T)=σ(T)\σe(T),即σd(T)是全体有限维的孤立的特征值点.
定义1.5[4]令T Hilbert空间H上的闭的对称算子,We(T)={λ∈C|(Tλ-λI)-1是无界的,或者dim N(T-λI)=∞},称为T的本质谱核.
引理1[5]设函数区间[0,∞)上可积,且>0,则方程(-1)k(pn-k(x)y(k))(k)=λy,有这样的2n个线性无关的解y1,y2,…,y2n,当x→+∞时,它们的渐近性状如下:yk=eμkξ[1+o(1)],其中μk为(-1)nλ的所有不同的2n次方根,其实部是各不相同的,而
引理2[5]设函数′,p1,p2,…,pn在区间[0,∞)上可积,且>0,则算子T0的亏指数为(n,n).
引理3[5]一端奇异且亏指数为(n,n)的算子T0的任何自共轭扩张T被线性无关的边界条件
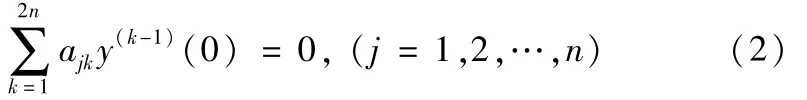
所确定,并且
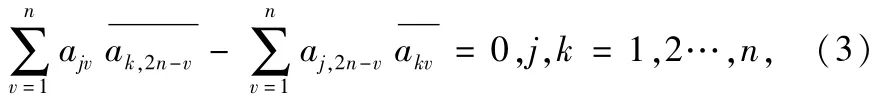
反之,一切满足条件(3)的线性无关条件(2),确定着算子T0的某个自共轭扩张.
引理4[4]设算子T是Hilbert空间H中闭的对称算子,则算子T是自共轭的充要条件是σ(T)⊂R.
引理5[4]算子T是Hilbert空间H上的自共轭算子,则σr(T)=φ.
引理6[5]如果对于实数λ,方程l(y)=λy在L2[0,∞)中的线性无关解的个数小于算子T0的亏指数,则这个值λ属于算子T0的谱的核.因此,如果这个值λ不是算子T0的特征值,则它属于T0的所有自共轭扩展谱的连续部分.如果端点a或端点b中之一是正则的,那么,后者总是成立的.
引理7[5]设算子T是Hilbert空间H中闭的对称算子,如果T是自共轭算子,则We(T)=σe(T)={λ∈C|(Tλ-Iλ)-1是无界的,或者dim(T-λI)=∞},即当T是自共轭算子时,它的本质谱核和本质谱是重合的.
引理8[5]算子T0的任何自轭扩张的豫解式Rλ是积分算子,它具如下形式:
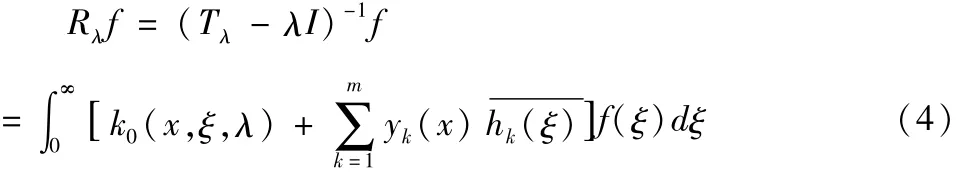
其中

m为最小算子T0的亏指数.
2 主要结论

定理若(1)式的系数满足(I),定义域和边值条件满足(II),则由生成的算子T是一个自共轭算子,它的本质谱充满正实轴;而在负半轴R-[0,∞)上只有算子T的离散谱.
证明:根据引理1得,对∀λ∈C,方程

有2n个线性无关的解yk(k=1,2,3,…,2n);当x→∞时,它们的渐近性状如下:

其中μk为(-1)nλ的所有不同的2n次方根,其实部各不相同,而=-λ,k=1,2,…,n,从而当x→∞时,

由引理2知微分算式(1)生成的最小算子T0的亏指数为(n,n),由引理3知微分算式(1)在边界条件3)下生成的算子T是一个自共轭算子,由引理4和引理5知其谱分为:σ(T)=σp(T)∪σc(T)⊂R,再由定义1.4知其谱分为:σ(T)=σd(T)∪σe(T)⊂R,下面分情况讨论上述自共轭算子T的谱分布:
(1)当λ∈[0,∞)时
因Reλ>0,且argλ=0,则μk=seiθk(k=0,1,…∈,2n-1),其中
当n为偶数时

当n为奇数时
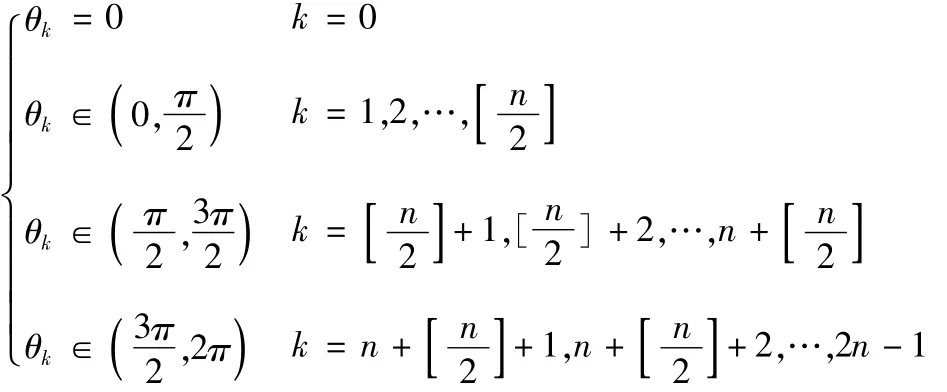
根据这2n个角θk(k=0,1,…,2n-1)在平面直角坐标系中的分布,按μk的实部进行排序.
Reμ1≤Reμ2≤…≤Reμn-1<0≤Reμn+1≤Reμn+2…≤Reμ2n
设ρi=Reμi.当1≤i≤n-1时,ρi=Reμi<0,yi=eμiξ[1+o(1)]∈L2[0,∞),当n≤i≤2n时,ρi=Reμi≥0,yi=eμiξ[1+o(1)]∉L2[0,∞),故当λ∈[0,∞)时,方程(6)在L2[0,∞)中的线性无关解的个数为n-1小于其最小算子T0的亏指数n,由引理6知这时λ属于算子T谱的连续部分.为了证明定理的前半部分,由引理7知,只要证明当λ∈[0,∞)时,算子T的豫解算子无界即可.
由引理2可知其最小算子T0的亏指数为n,因此由引理8得到其任何自轭扩张的算子豫解式Rλ是个积分算子,它具如下形式:


由上面推导过程可知,当λ∈[0,∞)时,方程(6)在L2[0,∞)中的线性无关解的个数只有n-1个,小于最小算子T0的亏指数n,所以y1(x),y2(x),y3(x),…,yn(x)中只有n-1个属于L2[0,∞),有一个yk(x)∉L2[0,∞),所以y1(x),y2(x),y3(x),…,yn(x)的任何线性组合也不属于∞,所以当λ∈[0,∞)时,其豫解算子(Tλ-λI)-1是无界的,由引理7知λ∈[0,∞)时,属于自共轭算子T的本质谱,即算子T的本质谱充满正实轴,这就证得了定理的前半部分.
(2)当λ∈R-[0,∞)时
因为Reλ<0,且argλ=π,μk=seiθk(k=0,1,…∈,2n-1),其中所以
当n为奇数时

根据这2n个角θk(k=0,1,…,2n-1)在平面直角坐标系中的分布,对μk的实部进行排序.
Reμ1≤Reμ2≤…≤Reμn<0≤Reμn+1≤Reμn+2…≤Reμ2n
设ρi=Reμi.当1≤i≤n时,ρi=Reμi<0,yi=eμiξ[1+o(1)]∈L2[0,∞),当n+1≤i≤2n时,ρi=Reμi>0,yi=eμiξ[1+o(1)]∉L2[0,∞),故当λ∈R-[0,∞)时,方程(6)在L2[0,∞)中的线性无关解的个数等于其最小算子T0的亏指数n.下面我们证这时只有算子T的离散谱,即只要证当λ∈R-[0,∞)时,算子T的豫解算子有界即可.
由引理8知算子T的豫解算子Rλ是个积分算子,它是以G(x,ξ,λ)=k0(x,ξ,λ)为核的积分算子,对区间[0,∞)中的一切x,任意固定的ξ,当x>ξ时,核G(x,ξ,λ)为y1(x),y2(x),y3(x),…,yn(x)的线性组合,即

由上面推导过程可知,当λ∈R-[0,∞)时,方程(6)在L2[0,∞)中的线性无关解的个数等于其最小算子T0的亏指数n,所以y1(x),y2(x),y3(x),…,yn(x)全部属于L2[0,∞),故它们的线性组合也属于L2[0,∞),故,所以当λ∈R-[0,∞)时,算子T的豫解算子(Tλ-λI)-1有界,所以当λ∈R-[0,∞)时,算子T只有离散谱,这就证得了定理的后半部分.
综合(1)、(2),定理得证.
推论[2]微分表达式:
l(y)=(-1)n(p(x)y(n)(x))(n)+q(x)y(x)(10)当p(x),q(x)均为实值函数,且p(x),q(x)∈L2[0,∞)时,那么由上式在L2[0,∞)内生成的任何自伴算子是下有界的,它的本质谱充满正实轴,在负半轴上只有离散谱.
本文只是在特殊情形下对高阶自共轭微分算子的谱进行了定量分析,要想对任意自共轭微分算子谱进行定量分析,是一件很不容易的事情;但是随着计算机的迅速发展,我们可以借助于计算机模拟,这方面的研究将会取得很大的进展.
[1]孙炯,王忠.常微分算子谱的定性分析[J].数学进展,1995,(24):406-422.
[2]王忠.具有可积系数J-对称微分算子的亏指数[J].内蒙古大学学报(自然科学版),1998,(5):607.
[3]王忠,付守忠.线性算子谱理论及其应用[M].北京:科学出版社,2013.
[4]孙炯,王忠.线性算子的谱分析[M].北京:科学出版社,2005.
[5]Naimark M A.线性微分算子[M].北京:科学出版社,1964.
Quantitative Analysis of the Spectrum of a Class of High Order Self Conjugate Differential Operators
QIAN Zhixiang
(The Department of Basic Education,Zhaoqing Science and Technology Polytechnic,Zhaoqing Guangdong 526100,China)
The paper quantitatively analyzes the spectrum of a class of high order self conjugate differential operators.It is indicated that their essential spectrum covers the entire positive semi-axisλ≥0 and there is only discrete spectrum in the negative semi-axis. Key W ords:differential expression;symmetric differential operator;self conjugate differential operator;discrete spectrum;essential spectrum;spectral analysis
O175.3
A
1008-4681(2014)02-0011-04
(责任编校:晴川)
2014-01-06
广东省高层次人才培养项目(批准号:9251064101000015).
钱志祥(1974-),男,安徽巢湖人,肇庆科技职业技术学院基础教学部讲师,硕士.研究方向:微分算子理论.
