改进的基于支持向量机模型剪接位点的预测

王丽美，郑大军，郑程友

(1.临沧师范高等专科学校数理系，云南临沧677000；2.福建农林大学计算机与信息学院，福建福州350002；3.桂林理工大学机械与控制工程学院，广西桂林541000)

改进的基于支持向量机模型剪接位点的预测

王丽美1，郑大军2，郑程友3

(1.临沧师范高等专科学校数理系，云南临沧677000；2.福建农林大学计算机与信息学院，福建福州350002；3.桂林理工大学机械与控制工程学院，广西桂林541000)

在采用概率编码的基础上，利用支持向量机模型对人类剪接位点进行预测，重点研究了基于核主成分分析方法对最终预测模型的影响.从实验结果看，这种改进的基于支持向量机模型剪接位点的预测在敏感性和特异性上优于其他模型.

剪接；预测；特征提取；支持向量机；核主成分分析

Brunak[11]等人采用了神经元网络模型来识别剪接位点；Castelo[12]等人则在识别剪接位点的过程中采用了Bayesian网络模型；Haussler[13]等人尝试了隐马尔科夫模型，并取得了不错的识别效果.

Staden采用权重矩阵模型来对剪接位点进行分析[14]，该模型假设各个位点的碱基是相互独立的，其出现的概率是由位置决定的，与前后的碱基无关；Zhang和Marr采用权重阵列模型[3]，该方法可以看成是权重矩阵模型的扩展，它放宽了碱基间独立的限制，研究了碱基间的相互依赖关系，可以把它看作是一个一阶马尔科夫模型；Salzberg[15]利用条件概率模型对剪接位点以及起始转录点进行识别；Burge[16]在对剪接位点的识别中提出了最大相关分解的思路，该模型能够得到非相邻位点碱基的相关性，取得了不错的效果.

Wang[17-18]等利用改进的神经网络来对剪接位点

剪接位点的识别主要包括传统的生物学实验方法和计算机算法的方法.传统的生物学实验的结果准确，但是成本较高，会消耗大量的人力物力，因此限制了它的大规模使用；而基于计算机算法的研究方法代价则小得多，但是具体的识别精度要低于传统的生物学实验的方法.

剪接位点识别最初是利用生物学实验的方法，这也是最基本可靠的方法.但近年来计算机技术和生物科学技术发展迅速，使生物学数据的爆炸性增长，给剪接位点的识别带来了巨大的挑战.在这种背景下，传统的生物学实验的方法远远不能满足人们的要求.所以，人们开始尝试采用统计学、数学模型、模式识别等方法来建立预测模型，并将其在计算机上实现，以加快实验的进程.

目前剪接位点预测中所采用的主要方法有MM模型(Markov Model)[1]、WMM模型(WeightMatrixModel)[2]、WAM模型(Weight Array Model)[3]、MEM模型(Maximum Entropy Model)[4]、MDD模型(Maximum Dependence Decomposition Model)[5]、IDQD(Incrementof进行识别，他们把模式识别和组分模式结合起来；Xia[19]等引入竞争机制对可变剪接位点进行识别，供体端的识别率为89.21%，受体端的识别率为87.98%；Zhang[6]等采用多样性指标的二次判别方法预测人类基因组中的组成性剪接位点.

Degroeve[9]等在对剪接位点的识别中考虑到了组成特征、位置特征以及密码子偏好性等.

除了以上介绍的这些算法外，还有BRAIN (Batch Relevance-based Artificial Intelligence)学习算法、motif方法等.

本文主要是使用核主成分的方法来进行剪切位点数据的特征提取，然后利用支持向量机的方法分别对供体剪接位点和受体剪接位点建立预测模型.

1 核主成分分析

假设x1,x2,...,xM为训练样本，用{} xi表示输入空间.KPCA方法的基本思想是通过某种隐式方式将输入空间映射到某个高维空间(常称为特征空间)，并且在特征空间中实现PCA.假设相应的映射为Φ，其定义如下：

核函数通过映射Φ将隐式实现点x到F的映射，并且由此映射而得的特征空间中数据满足中心化的条件，即

则特征空间中的协方差矩阵为：

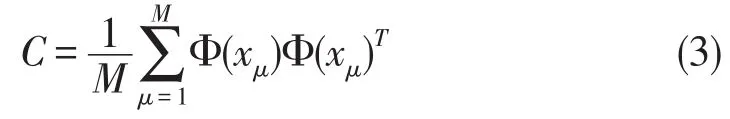
现求C的特征值λ≥0和特征向量

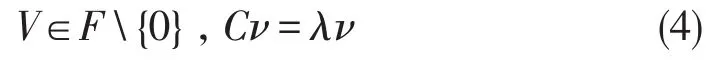
即有

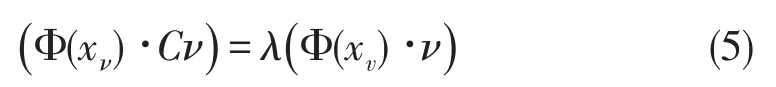
考虑到所有的特征向量可表示为Φ(x1),Φ(x2),...,Φ(xM)的线性张成，即

则有

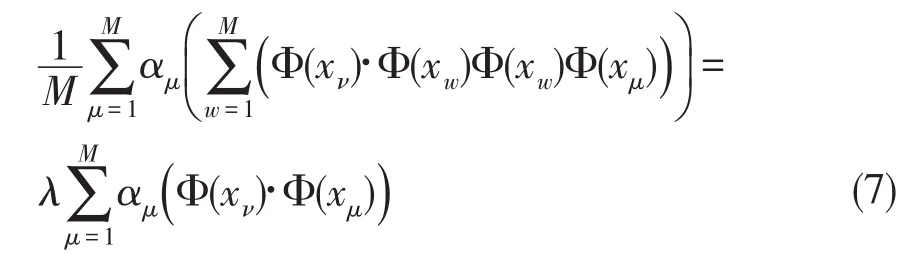
其中v=1,2,…,M.定义M×M维矩阵K：

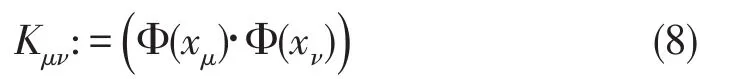
则式子(7)可以简化为

显然满足

求解(10)就能得到特征值和特征向量，对于测试样本在特征向量空间Vk的投影为

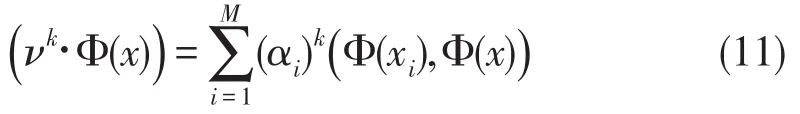
将内积用核函数替换则有

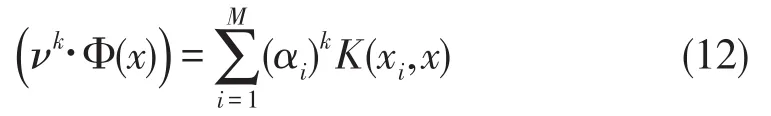
当(2)不成立时，需进行调整，

则核矩阵可修正为

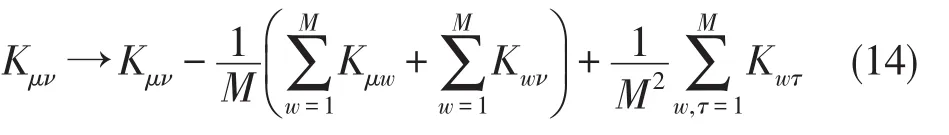
2 支持向量机

支持向量机[18]是机器学习的一种方法，能够有效地处理模式识别和回归等复杂的问题.另外，将其推广之后，还可以在预测和评价等问题中得到应用.支持向量机属于一般化线性分类器，被称为最大边缘区域分类器.

假定有训练样本集

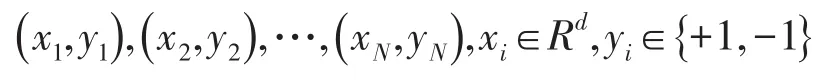
其中，每个样本都是d维向量，变量y是类别标签. w1类用+1表示，w2类用-1表示.而且，这些样本所组成的数据集是线性可分的，也就是存在一个超平面

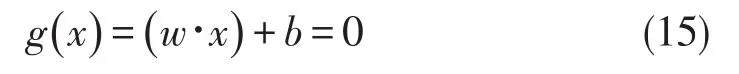
能够把所有的N个样本都没有错误地分开.这里，w∈Rd是线性判别函数的权值，b是其中的常数项. (w∙x)表示向量w与x的内积，即w'x.

定义：一个超平面，如果它能够将训练样本没有错误地分开，并且这两类训练样本中离超平面最近的样本与超平面之间的距离是最大的，则把这个超平面称作最优分类超平面(optional seperating hyperplane)，简称最优超平面(optionalhyperplane).两类样本中离分类面最近的样本到分类面的距离称作分类间隔(margin)，最优超平面也称作最大间隔超平面.

最优超平面定义的分类决策函数为

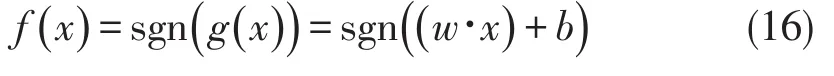
其中，sgn()为符号函数，当自变量为正值时函数取值为1，自变量为负值时函数取值为-1.

所有N个样本都可以被超平面没有错误地分开，就是要求所有样本都满足

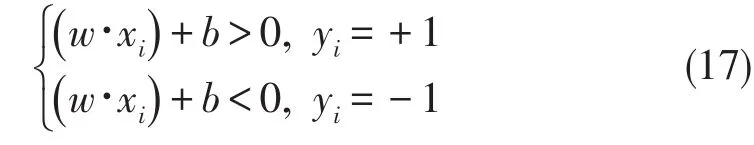
既然尺度可以调整，把式(17)的条件变成

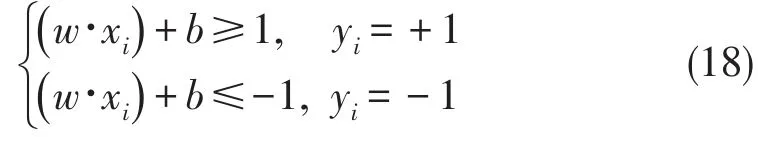
即要求第一类样本中g(x)最小等于1，而第二类样本中g(x)最大等于-1.把样本的类别标号y值乘到不等式(16)中，可以把两个不等式合并成一个统一的形式：

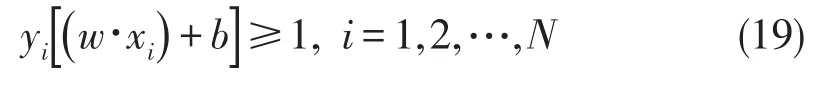
用此条件约束分类超平面的权值尺度变化，这种超平面称作规范化的分类超平面(the canonical form of the separating hyperplane).g(x)=1和g(x)=-1就是过两类中各自离分类面最近的样本且与分类面平行的两个边界超平面.

由于限制两类离分类面最近的样本g(x)分别等于1和-1，那么分类间隔就是.于是，求解最优超平面的问题就成为

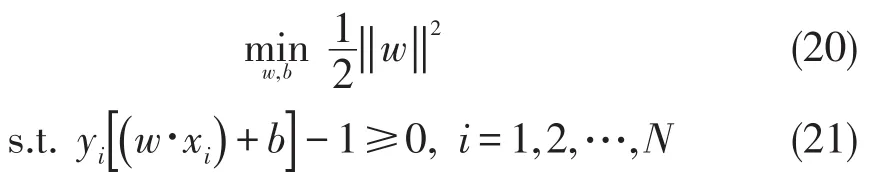
这是一个在不等式约束下的优化问题，可以通过拉格朗日法求解.对每个样本引入一个拉格朗日系数可以把式(20)和式(21)的优化问题等价地转化为下面的问题

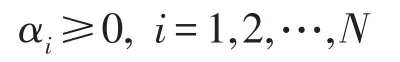
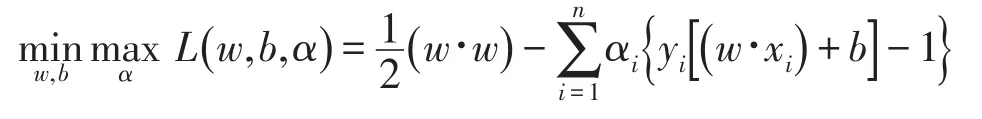
式中的L(w,b,α)是拉格朗日泛函，式(20)、式(21)的解等价于式(23)对w和b求最小，而对α求最大，最优解在L(w,b,α)的鞍点上取得.

在式(21)的鞍点处，目标函数L(w,b,α)对w和b的偏导数为零，由此可以得到，对最优解，有

且

将式(22)和式(23)带入拉格朗日泛函中可以得到，式(20)、式(21)的最优超平面问题的解等价于下面的优化问题的解

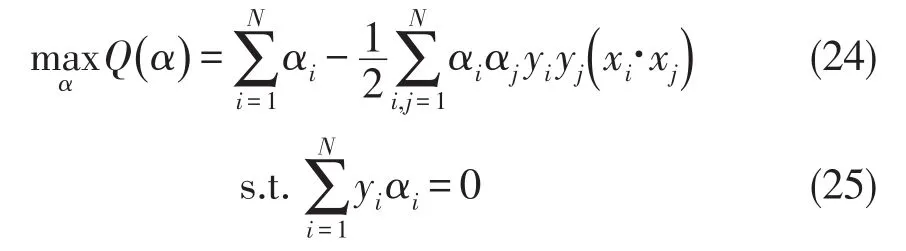
且

这是一个对αi,i=1,2,…,N的二次优化问题，称作最优超平面的对偶问题(the dualproblem)，而式(20)、式(21)的优化问题称作对偶超平面的原问题(the primary problem).通过对偶问题的解i=1,2,…,N，可以求出原问题的解

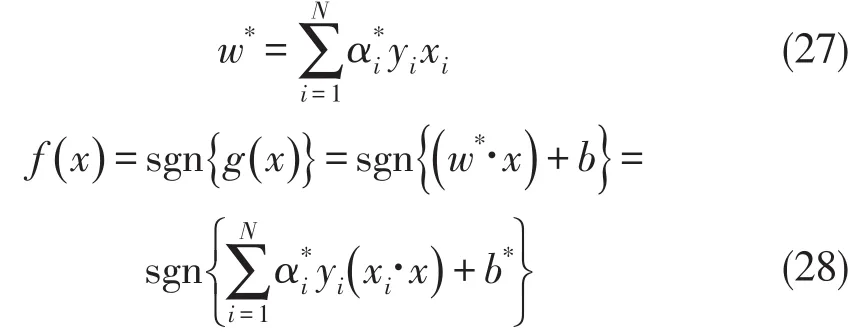
现在来看b*的求解问题.

根据最优化理论中的库恩-塔克(Kuhn-Tucker)条件，式(23)中的拉格朗日泛函的鞍点处满足

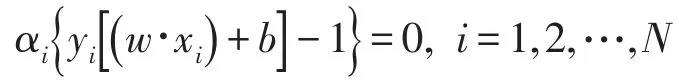
再考虑到式(21)和式(22)，可以看到，对于满足式(22)中大于号的样本，必定有αi=0.而只有那些使式(21)中等号成立的样本所对应的αi才会大于0.这些样本就是离分类面最近的那些样本，是这些样本决定了最终的最优超平面的位置；在式(27)和式(28)的加权求和中，实际也只有这些αi＞0的样本参与求和.这些样本被称作支持向量(supportvectors)，它们往往只是训练样本中的很少一部分.

对于这些支持向量来说，有

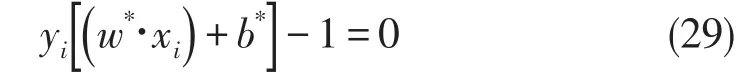
因为已经求出了w*，所以b*可以用任何一个支持向量根据式(29)的方程求得.在实际的数值计算中，通常采用所有αi非零的样本用式(29)求解b*后再取平均.

上面提到的线性支持向量机，它求解的分类器为：

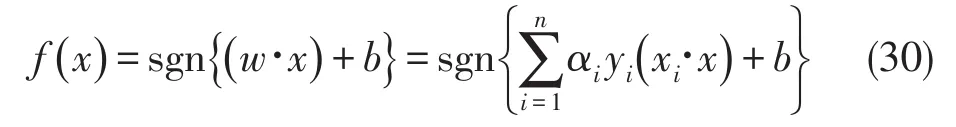
其中的αi,i=1,2,…,N是下列二次优化问题的解

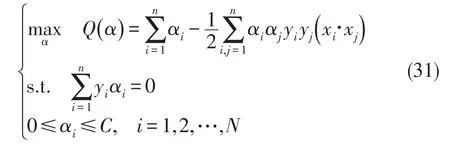
b通过使

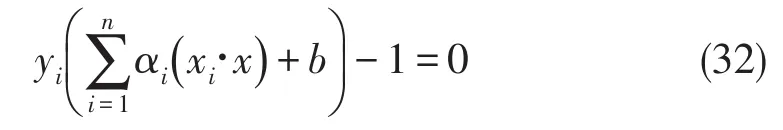
成立的样本(即支持向量)求得.

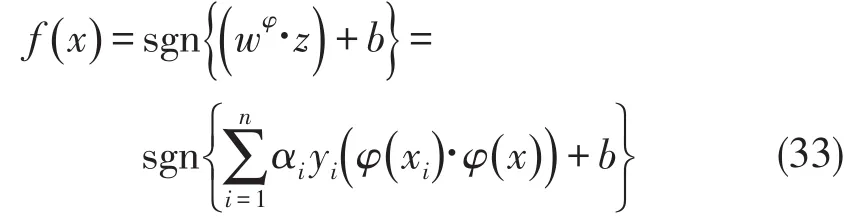
而相应的优化函数问题变成

定义支持向量的等式成为

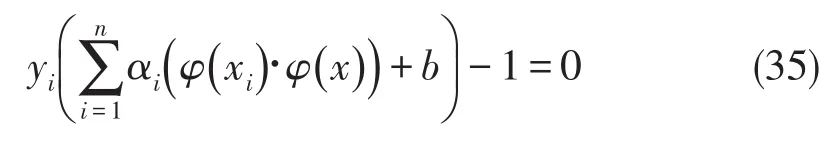
仔细观察这些公式会发现，在进行变换后，无论变换的具体形式如何，变换对支持向量机的影响是把两个样本在原特征空间中的内积(xi∙xj)变成了在新空间中的内积(φ(xi)∙φ(xj)).新空间中的内积也是原特征的函数，可以记作

把它称作核函数.这样，变换空间里的支持向量机就可以写成

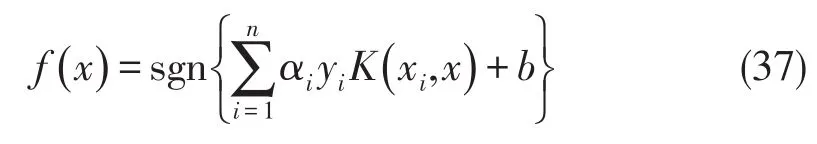
其中，系数α是下列优化问题的解

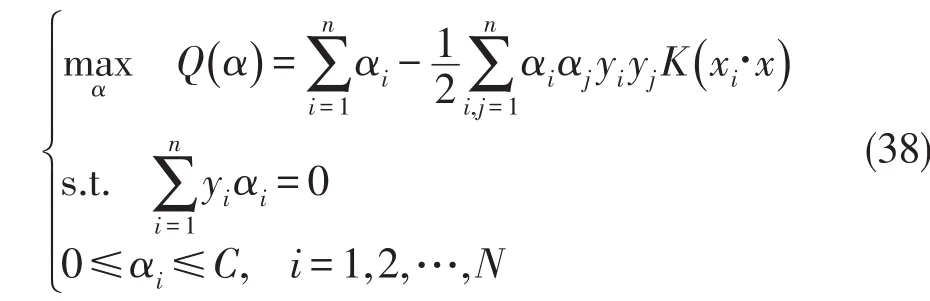
b通过满足下式的样本(支持向量)求得

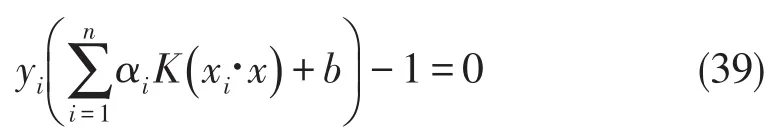
泛函空间的有关理论表明这样做是完全可行的，条件是需要找到能够构成某一变换空间的内积核函数.Mercer定理给出了这一条件：

定理(Mercer条件)对于任意的对称函数K(x,x')，它是某个特征空间中的内积运算的充分必要条件是，对于任意的φ≠0且∫φ2(x) d x＜∞，有

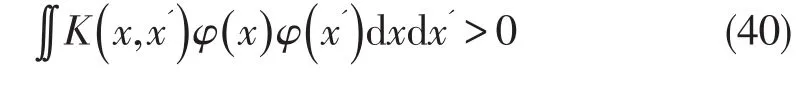
因此，选择一个满足Mercer条件的核函数，就可以构建非线性的支持向量机.进一步可以证明，这个条件还可以放松为满足如下条件的正定核(posi-是定义在空间X上的对称函数，且对任意的训练数据x1,…,xm∈X和任意的实系数a1,…,am∈R，都有

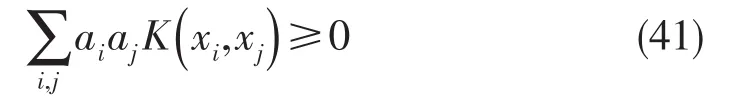
对于满足正定条件的核函数，肯定存在一个从X空间到内积空间H的变换φ(x)，使得

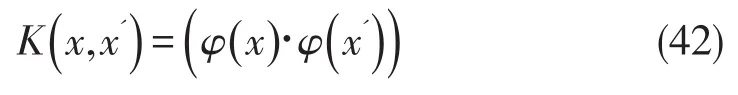
这样构成的空间是在泛函中定义的所谓可再生核希尔伯特空间RKHS(reproducing kernel Hilbert space).

采用不同的核函数就得到不同形式的非线性支持向量机.

支持向量机的基本思想可以概括为：首先通过非线性变换将输入空间变换到一个高维空间，然后在这个新空间中求最优分类面即最大间隔分类面，而这种非线性变换是通过定义适当的内积核函数实现的.

支持向量机求得的分类函数，形式上类似于一个神经网络，其输出是若干中间层节点的线性组合，而每一个中间层节点对应于输入样本与一个支持向量机的内积，因此早期也被叫做支持向量网络.

3 基于支持向量机模型剪接位点的预测

3.1 编码方式

为了能够充分利用原始的碱基位点的数据的信息[20]，不采用直接编码的方式，而是分别统计真实的供体位点、虚假的供体位点、真实的受体位点、虚假的受体位点这些碱基序列在各位点上A、T、C、G四种碱基出现的相对频率.

然后，具体的在供体位点的编码方式上，取真实的供体位点序列各位点上四种碱基出现的相对频率和虚假的供体位点序列各位点上四种碱基出现的相对频率的差值，就可以得到一个相对频率差的矩阵，将这个矩阵作为供体位点序列的编码依据；同样地，将真实的受体位点序列各位点上四种碱基出现的相对频率和虚假的受体位点序列各位点上四种碱基出现的相对频率的差值矩阵作为受体位点序列的编码依据[10]，如表1、表2所示.

表1 供体位点编码矩阵部分示意图

表2 受体位点编码矩阵部分示意图

3.2 基因剪接位点预测评价体系

为了确定预测模型的好坏，需要一些标准来对其进行衡量，本文采用最广泛通用的评价体系，即：敏感性Sn、特异性Sp、准确度ACC和相关性系数MCC值.下面，定义一些变量，以便计算所需要的评价指标：

TP：True Positive，即真阳性的数目；

TN：True Negative，即真阴性的数目；

FP：False Positive，即假阳性的数目；

FN：False Negative，即假阴性的数目.

那么，Sn、Sp、ACC及MCC可以表示为：

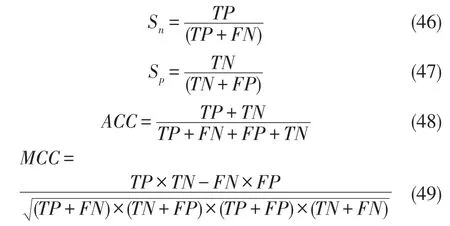
根据上述公式，可以得出：Sn是真实的剪接位点被识别正确的比率；Sp是虚假的剪接位点被识别正确的比率；ACC是剪接位点识别正确的比率；MCC是真实剪接位点和虚假剪接位点的相性.

在实际情况中，当Sn、Sp达到一定的值后，往往会具有负相关的关系.也就是说，当到达一定程度之后，Sn继续增加，同时假阴性也随之增加；当到达一定程度之后，Sp继续增加，同时假阳性也随之增加.

3.3 特征描述和预测模型的建立

核主成分分析实际上是在主成分分析的基础上进行的拓展的方法.它是在特征空间进行的主成分分析.具体的实验数据，真实的的供体位点和虚假的供体位点的个数都随机取2 000个，采用十倍交叉验证的方法；同样地，随机取真实的受体位点和虚假的受体位点各2 000个.另外，主成分分析的贡献率的阈值设置为90%，经过试验验证，在供体位点的实验中，选取3阶多项式核主成分分析的方法，可以得到选取的特征为82个；在受体位点的实验中，选取线性核主成分分析的方法，可以得到选取的特征为83个.

3.4 实验结果与分析

通过实验分别得出多项式核主成分和支持向量机模型对供体位点的识别结果、线性核主成分和支持向量机模型对受体位点的识别结果，如表3、表4所示.

由表3、表4得到的结果可以看出，在交叉验证实验中，无论是供体位点还是受体位点均在敏感性Sn、特异性Sp上保持了稳定性，波动始终在一个合理的范围，说明这个改进的模型是稳定和有效的.并且，可以得到供体位点预测结果平均为Sn=0.951，Sp=0.93；受体位点的预测结果平均值为Sn= 0.9305,Sp=0.913.在供体位点预测模型方面，基于多项式核主成分分析的特征提取方式相比较其他的模型都取得了更加出色的预测效果；在受体位点预测模型方面，基于线性核主成分分析的特征方式相比较其他的模型都取得了更加出色的预测效果.

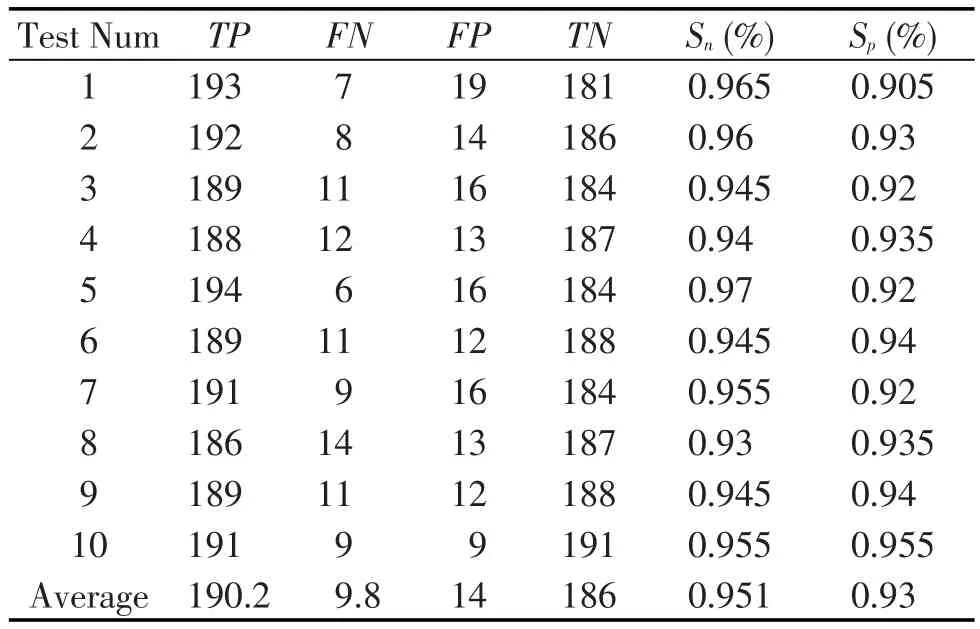
表3 多项式核主成分和支持向量机模型对供体位点的识别结果

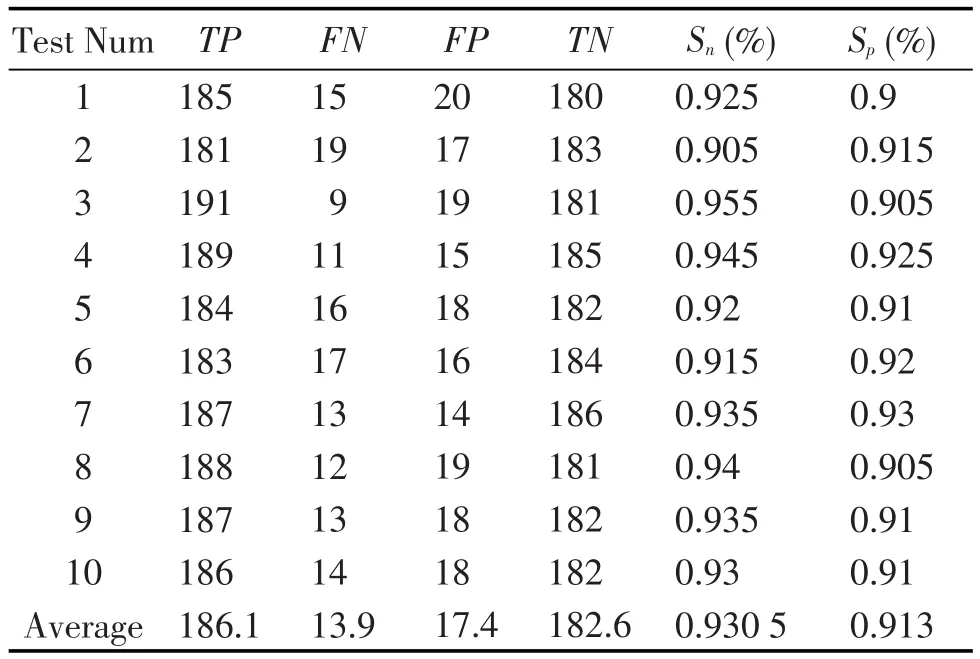
表4 线性核主成分和支持向量机模型对受体位点的识别结果

4 总结

本文在采用概率编码的基础上，利用支持向量机模型对人类剪接位点进行预测，重点研究了基于核主成分分析方法对最终的预测模型的影响.从实验结果看，这种改进的基于支持向量机模型剪接位点的预测从敏感性和特异性都优于其他模型.在特征描述的过程中是需要大量的运算时间，比普通的预测模型的时间复杂度要高.下一步的工作要能够在保证算法精度的情况下，尽可能的提高算法效率.

[1]Liu L,Ho Y K,Yau S.Prediction of primate splice site using inhomogeneous Markov chain and neural network[J].DNA and Cell Biology,2007,26(7):477-483.

[2]Staden R.The current status and portability of our sequence handling software[J].Nucleic AcidsResearch,1986,14(1):217-231.

[3]Zhang M,Marr TG.A weightarraymethod for splicing signal analysis[J].Computer Applications in the Biosciences:CABIOS,1993,9 (5):499-509.

[4]Yeo G,Burge C B.Maximum entropy modeling of short sequence motifswith applications to RNA splicing signals[J].Journal of Computational Biology,2004,11(2-3):377-394.

[5]Pertea M,Lin X,Salzberg S L.GeneSplicer:a new computational method for splice site prediction[J].Nucleic Acids Research,2001, 29(5):1185-1190.

[6]Zhang L,Luo L.Splice site prediction with quadratic discriminant analysis using diversitymeasure[J].Nucleic Acids Research,2003, 31(21):6214-6220.

[7]Chen TM,Lu C C,LiW H.Prediction of splice sites with dependency graphsand theirexpanded bayesian networks[J].Bioinformatics,2005,21(4):471-482.

[8]Brunak S,Engelbrecht J,Knudsen S.Neuralnetwork detects errors in the assignment of mRNA splice sites[J].Nucleic Acids Research,1990,18(16):4797-4801.

[9]Degroeve S,Saeys Y,De Baets B,etal.Splice Machine:predicting splice sites from high-dimensional local context representations[J]. Bioinformatics,2005,21(8):1332-1338.

[10]王勇献,王正华.生物信息学导论[M].清华大学出版社,2011.

[11]Brunak S,Engelbrecht J,Knudsen S.Prediction of human mRNA donor and acceptor sites from the DNA sequence[J].Journal of Molecular Biology,1991,220(1):49-65.

[12]Castelo R,GuigóR.Splice site identification by idlBNs[J].Bioinformatics,2004,20(suppl1):i69-i76.

[13]Haussler D K D,Eeckman M GR FH.A generalized hidden Markovmodel for the recognition of human genes in DNA[C]//Proc Int Conf on Intelligent Systems for Molecular Biology,St Louis,1996: 134-142.

[14]Staden R,McLachian A.Codon preference and its use in identifying protein coding regions in long DNA sequences[J].Nucleic AcidsResearch,1982,10(1):141-156.

[15]Salzberg SL.Amethod for identifying splice sites and translational startsites in eukaryoticmRNA[J].Computer applications in the biosciences:CABIOS,1997,13(4):365-376.

[16]Burge C B.Identification of Genes in Human Genomic DNA[D]. Stanford:Stanford University,1997.

[17]Wang M,Marín A.Characterization and prediction of alternative splice sites[J].Gene,2006,366(2):219-227.

[18]余萍.基于支持向量机发展的研究[J].新课程:教育学术,2011 (5):65-65.

[19]Xia H,Bi J,Li Y.Identification of alternative 5′/3′splice sites based on themechanism of splice site competition[J].Nucleic AcidsResearch,2006,34(21):6305-6313.

[20]黄金艳,李通化,陈开.基于知识编码的剪切位点预测[J].同济大学学报:自然科学版,2008,35(11):1548-1551.

【编校：许洁】

Prediction on Slice Site Based on Improved SVM Model

WANG Limei1,ZHENGDajun2,ZHENGChengyou3
(1.DepartmentofMathematicsand Physics,Lincang Teachers'College,Lincang,Yunnan 677000,China;2.CollegeofComputer and Information Technology,Fujian Agriculture and Forestry University,Fuzhou,Fujian 350002,China;3.College ofMechanicaland Control Engineering,Guilin University ofTechnology,Guilin,Guangxi541000,China)

By adopting probability encoding,the support vectormachine(SVM)modelwas used tomake a prediction on human's slice site and the impact of KPCAmethod on the final predictionmodelwas discussed.The experiment shows that this improved SVMmodel issuperior to othermodels in sensitivity and specificity on the prediction ofslice site.

slice;prediction;featureextraction;SVM;KPC Diversity with Quadratic Discriminant analysis)[6]、BN模型(Bayesian Network)[7]、NN模型(Neural Network，NN)[8]、SVM模型(SupportVectorMachine)[9-10]，等等.

TP301.6

A

1671-5365(2014)12-0093-06

2014-06-17修回：2014-08-21

王丽美(1987-)，助教，硕士，研究方向为数据挖据、生物信息

时间：2014-08-22 15:23

http://www.cnki.net/kcms/detail/51.1630.Z.20140822.1523.007.htm l