基于一种改进EMD算法的GPS多径效应抑制方法

崔冰波，陈熙源

（东南大学 仪器科学与工程学院，南京 210096）

基于一种改进EMD算法的GPS多径效应抑制方法

崔冰波，陈熙源

（东南大学 仪器科学与工程学院，南京 210096）

为了抑制短基线双差分GPS测量中的多径误差，提出了一种改进的经验模态分解(EMD)滤波方法。首先分析了含噪信号EMD分解的噪声传播特性，提出应用噪声辅助数据分析方法对低阶模态分量进行处理，实现将信号的噪声压缩至低阶本征模态函数(IMF)中，进而提高含噪信号高阶模态分量的信噪比。然后基于上述改进的EMD算法实现了模态单元阈值降噪，随机采样第1阶IMF构造多个具有相同信噪比的序列，最后平均处理多个序列的降噪结果以消除EMD分解的位置敏感性误差，与小波降噪以及传统EMD阈值降噪的仿真对比表明，提出的降噪算法有显著优势。最后，将提出的算法用于GPS测量信号的多径误差提取，结果表明该方法可以用于抑制短基线GPS测量的多径误差。

经验模态分解；多径效应；GPS；小波降噪

随着微电子技术和信号处理技术的发展，基于GPS接收机内部实时信号处理的各种滤波算法正成为多径抑制的主要方法[1]。小波变换具有多分辨率和良好的时频特性，近年来广泛应用于非平稳信号的处理，例如应用离散小波变换[2]和自适应小波变换[3]分析GPS 双差分测量信号以及基于平稳小波变换[4]抑制GPS多径信号都获得了较好的效果，但小波降噪需选择合适的小波基函数与分解层次，且针对不同的信号需选择不同的滤波参数，故而其适用性较差。经验模态分解(EMD)由Huang等人提出，是一种数据驱动的自适应时域分解方法，有很强的局部自适应分解特性，在一定程度上克服了小波分解的不足。虽然 EMD的理论基础尚不充分，但是由于其容易实现且总是获得良好的效果，所以其在非线性、非平稳信号处理中获得了广泛的关注。Chen等人采用EMD部分重构法对GPS的多径效应进行了研究[5]，由于该方法直接将含有噪声的模态分量去除，所以有可能在高信噪比的信号滤波中造成信号变形。Kopsinis等人基于平移不变小波变换思想提出一种基于 EMD模态单元的区间阈值滤波方法(Clear Iterative EMD Interval-Thresholding,EMD-CIIT)[6]，并且通过大量仿真实验说明该方法对低信噪比信号的除噪效果优于小波除噪，在一定程度上缓解了滤波中信号变形的问题，但由于其实现过程需要借助小波分析或者其它方法对高频分量处理，失去了EMD自适应分解的优势。为了提高EMD阈值滤波方法的适用性，本文提出了一种改进的 EMD滤波方法，并对模拟数据和 GPS观测数据进行了仿真实验，结果表明改进后的 EMD阈值滤波方法较小波降噪和EMD-CIIT除噪性能有显著改善。

1 多径效应

GPS接收机通过接收来自卫星（至少4颗）的广播星历信号，并测量信号传输延时，最终与光速相乘计算出与卫星的距离来实现GPS的定位功能。多径效应是指天线接收到的信号不仅包含卫星直射信号还包括接收机周围反射物反射的卫星信号，从而影响信号传输时间的测量结果，并最终影响GPS定位精度。目前抑制多径效应的方法主要包括：选择合适的接收机工作环境、采用先进的天线和接收机硬件技术以及应用自适应滤波技术等等，例如远离反射源，加装扼流圈天线，增加接收机的相关器个数等。这些技术都有一些的局限性，比如扼流圈的增加，不仅增加了接收机的成本、尺寸和重量，其对于来自天线上方的多径信号（比如高层建筑的反射信号）效果十分有限。双差分模型的 GPS定位技术能有效的规避系统的大部分具有相关特性的误差，比如卫星钟差、接收机钟差、电离层与对流层延迟等等，但是由于不同接收机的热噪声和多径误差不具有显著的相关性，所以无法通过双差分模型进行消除[7]。目前基于天线和接收机硬件的多径抑制方法虽然有一定的效果，但是增加了系统的成本，限制了其在民用领域的使用范围，使得多径误差仍然是短基线高精度差分定位的主要误差[8]。无论在静态基站应用还是动态接收机应用中，多径效应都带有明显的时变特性，所以固定结构的滤波设计无法对其有效处理。基于大多数情况下多径信号的变化缓慢的特性，对其采用EMD分析处理具有很大优势，可以近似认为多径信号存在于 EMD分解后的高阶模态函数和余项中。

2 改进的EMD

EMD将信号自适应的分解成具有物理意义的一组IMF，基于EMD的滤波方法都是基于IMF实现，所以改善IMF精确度是实现高效滤波的重要保证。目前 EMD滤波的应用研究主要集中在部分重构法、结合其它滤波方法（如小波变换）构造的组合滤波方法以及改进的模态单元阈值滤波方法，上述方法均在一定程度上提高了信号的信噪比，但是忽略了EMD 分解缺陷导致高频 IMF中含有少量信号微弱特征的情况，使它们不适用于高信噪比信号的降噪。

2.1 噪声估计

为了提高 EMD对含噪信号弱特征信息的辨识度，必须对低阶IMF的噪声水平进行分析。本文提出了一种基于奇异谱分析（Singular Spectrum Analysis，SSA）的方法对IMF分量进行噪声水平估计，SSA将一维时间序列映射到表征信号成分能量强度的多维空间[9]。基于多径信号缓慢正弦震荡的特征构造信号：

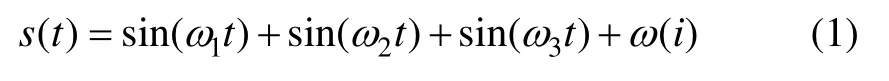
其中，ω(i)为噪声，模拟周期为几十秒到几十分钟的正弦振荡。

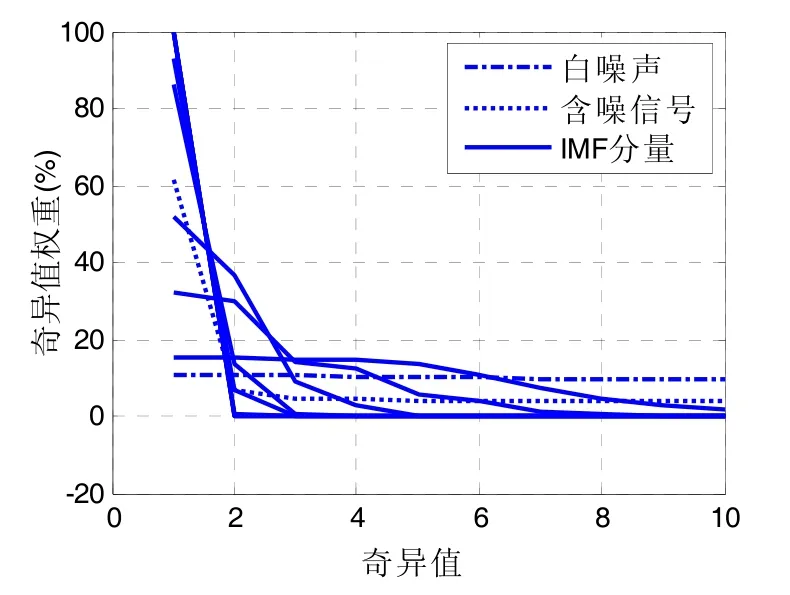
图1 含噪信号及其各阶IMF分量的奇异谱Fig.1 The SS of noisy signal and its IMFs

2.2 噪声压缩

为了解决EMD分解可能出现的小波消失、模态混叠等问题，Wu和Huang提出了基于整体平均经验模态分解（Ensemble Empirical Mode Decomposition,EEMD）的噪声辅助数据分析方法[10]，使分解得到的IMF能更准确反映真实物理意义，但EEMD需要进行几十甚至几百次 EMD的“筛选”运算，同时由于噪声的加入使其IMF分量的个数增加，使EEMD算法的运算量和后续处理工作量增大。

为了克服EEMD的上述缺陷，胡爱军等通过加入高频谐波来改变信号的极值分布，从而消除模态中的异常事件[11]，该方法在异常事件比较复杂时(比如随机噪声干扰下)谐波参数的选择需要进一步研究，算法适用性有待提高。仿真分析表明低阶IMF的分解结果对后续分解的影响较大，减少低阶IMF的分解误差可以显著的提高EMD分解精度。基于白噪声的零均值特性，可以对含噪信号加入白噪声，使更多的高频噪声在低阶IMF中分解出来，同时为了减少运算量，只对初步估计为噪声占优的 IMF分量进行噪声辅助数据分析。在确定了含噪信号y(t)的辅助分析阶数M、噪声标准差以及加噪次数I后，改进的分解算法的描述如下：

步骤①：初始化k,j，h(t)=y(t)，其中k是IMF的阶数,j是加噪次数；

步骤②：对h(t)加噪处理h(t)=y(t)+wn(t)，j=j+1；

步骤③：找出序列h(t)的全部极值，用三次样条插值构造序列的上下包络线u(t)、d(t)，计算包络均值m(t)=(u(t)+d(t))/2；

步骤④：求h(t)=h(t)-m(t)，判断h(t)是否满足停止条件，不满足则返回步骤③继续筛选，直至筛选出IMFkj，如满足结束本次筛选，返回步骤②继续加噪筛选过程直至j=I，；

图2为EMD、EEMD以及本文算法对式(1)模拟数据s(t)处理后的结果，可以发现由于噪声的加入EEMD较EMD增加了1个IMF，而本文算法较EMD减少了1阶IMF，这是由于在对低阶IMF进行噪声辅助分析后，基于白噪声的零均值特性，噪声被压缩到低阶IMF中，使得其对信号真实信息的影响减小，从而使分解得到的IMF物理意义更明确，这为后续提出的阈值滤波方法提供基础。

图3为三种方法分解后IMF分量的奇异谱效果，右上角为第 1个奇异值占该 IMF分量能量贡献占96.5%以上的放大效果图，可以发现EEMD分解得到的各IMF分量的区分度优于传统EMD分解结果，红色椭圆标记部分包含加入噪声引入的多余IMF分量。本文算法由于增加了低阶IMF的辅助噪声处理，使信号中的噪声转移到前2阶，并且由于低阶（1～2阶）IMF噪声特性更加明显，奇异值差别不大，使其奇异谱变得更加平坦。由于只对低阶IMF进行噪声辅助数据分析处理，本文算法得到的高阶IMF间区分度不如EEMD，但是算法的运算量明显少于EEMD，鉴于本文主要研究混有白噪声的 GPS双差分信号中多径信号的提取（假设处理的多径信号较噪声而言频率很低）的目的，不对低频的多种多径信号进行区分，故而此处对降噪效果并无影响。

3 阈值滤波

基于小波分析的阈值除噪是对不同尺度下小波系数（常为高频系数）的幅值进行阈值处理，由于IMF数据在过零点附近的幅值会小于任一大于零的阈值，所以幅值阈值滤波方法不适用于EMD阈值滤波。本文采用的是一种基于IMF相邻过零点区间极值特征的阈值滤波，即考虑IMF两过零点间的极值大小，如果极值大于阈值则保留该区间的全部幅值，否则该区间定性为噪声数据直接舍去，避免了基于IMF幅值进行阈值滤波造成的数据变形[6]。设含噪信号s(t)经改进后的EMD分解得到如下的形式:

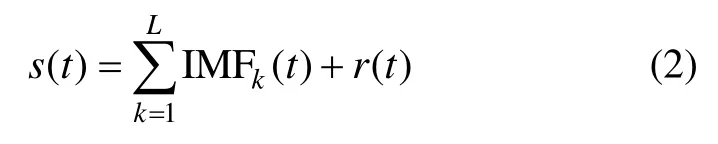
式中，L为分解得到的IMF阶数，r(t)为信号的余项，由于多径信号主要集中在高阶IMF中，所以可以通过下式求解除噪后的信号：

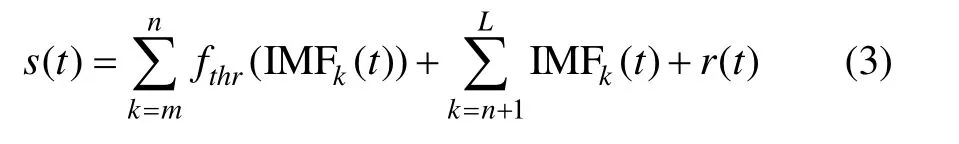
式中，fthr(·)为阈值滤波函数，m和n为需阈值处理的IMF阶次上下限，即等式右边第1项为阈值滤波后的IMF分量，其余项为信号中未经阈值处理的分量，其中k＜m的IMF直接舍去。考虑到EMD分解对随机噪声产生的位置具有敏感性，本文采用随机取样第1阶IMF数据的方式，构造多个与原数据有相同信噪比的新序列来消除位置敏感性带来的误差，本文没有借助其它滤波方法处理第1阶IMF，而是直接基于改进的EMD分解结果进行阈值滤波，其实现过程如下：

图2 EMD、EEMD及本文算法分解效果Fig.2 Decomposition effects of EMD、EEMD and proposed method

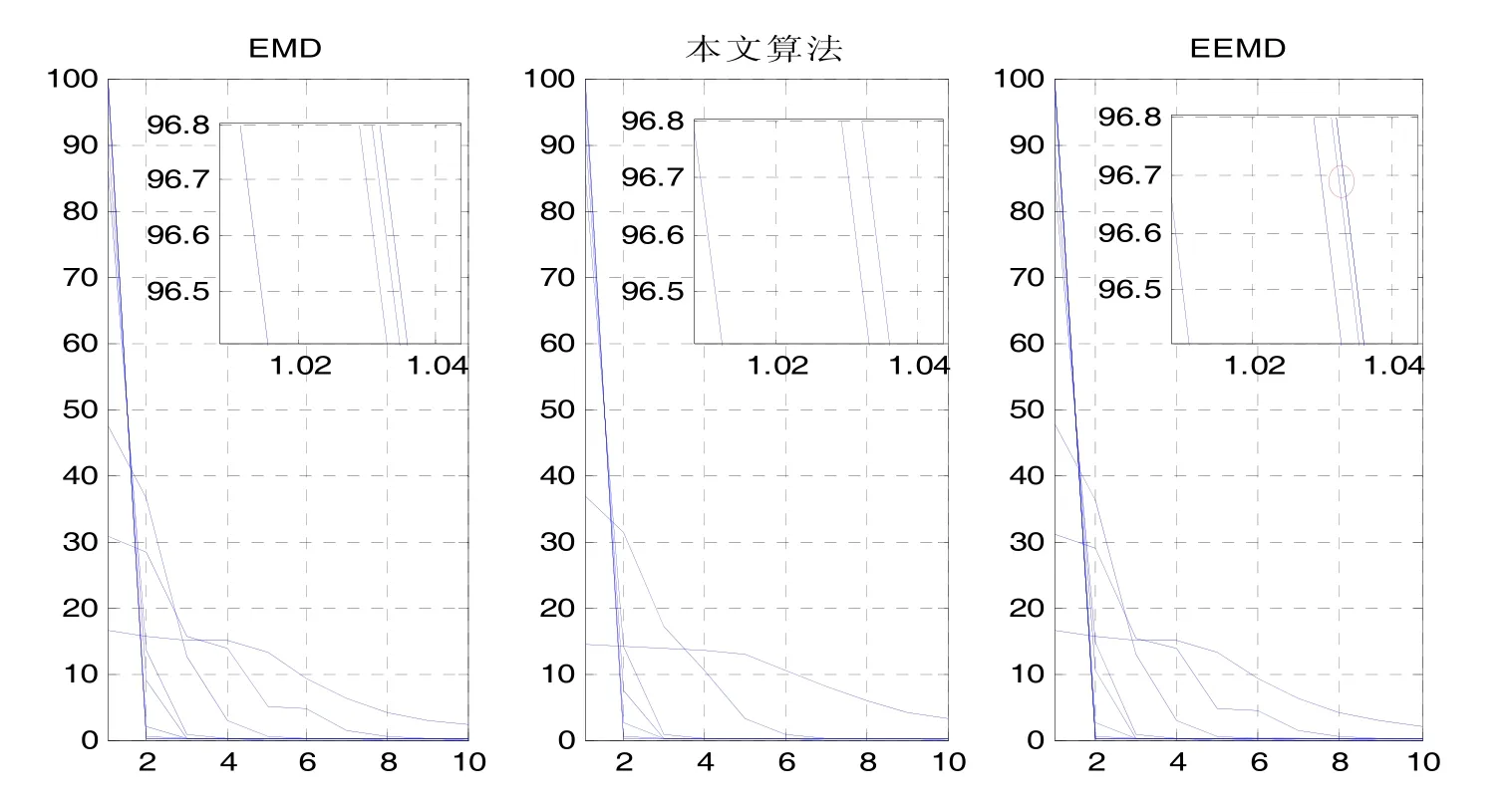
图3 三种方法IMF分量的奇异谱Fig.3 The SS of IMF components decomposed by the three methods

① 对s(t)进行改进的EMD分解，得到L阶IMF；

② 基于除IM1F外的其余L-1阶 IMF重构信号；

③ 通过随机采样(随机打乱或者循环移位)产生新的序列 alter(IMF1(t))，并构造与原序列有相同信噪比的；

⑤ 重复③和④K-1次，K为设定的迭代次数即为最终降噪后的信号；

4 仿真分析

4.1 模拟数据仿真

为了验证本文算法的效果，对四组不同频率特征的数据进行降噪处理，前三组为matlab中wnoise函数产生的doppler、blocks以及heavy sine，第四组为本文式(1)建立的仿真数据,序列的长度均为 1024，仿真过程分别加入不同噪声水平的高斯白噪声，模拟产生不同信噪比的含噪信号。分别采用 EMD-CIIT、小波降噪以及本文算法对信号进行降噪，三种方法均采用硬阈值法，阈值选择采用固定阈值(sqtwolog)（虽然这种阈值方案不是最优的，但是作为三种方法的除噪效果对比是可行的选择）。EMD-CIIT和本文算法的迭代数均为20，其中EMD-CIIT第1阶IMF的滤波选用小波降噪，本文算法对低阶IMF处理中的迭代次数为200次，辅助噪声方差0.01，噪声辅助处理的IMF阶数为2。小波降噪选择了3种小波基，其对应的表1中的结果，均是该小波基下基于最优分解层次的除噪效果。本文采用两种方法来对降噪效果进行评判，分别是均方误差和信噪比，其表达式分别如下所述：

① 均方误差

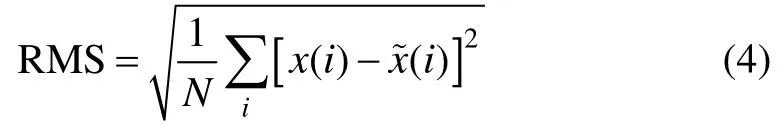
式中，x(i)为不含噪声的纯净信号，x～(i)为滤波降噪后的估计信号，均方误差越小，表明降噪效果越好。

② 信噪比

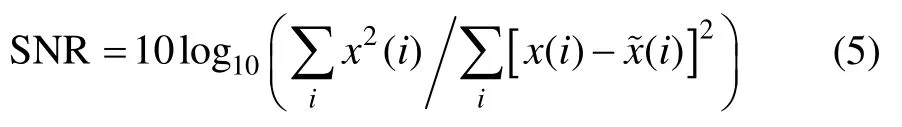
式中，分子为信号有效能量，分母为噪声有效能量，信噪比越高表明信号残留的噪声越少，其单位为dB。

仿真结果如表1所示，可以看出同一种含噪信号，在不同小波基下降噪效果是不同的，对不同频率的含噪信号，达到最优滤波效果的小波基也是不同的，所以小波降噪的参数选取与信号本身的特征有关。

为了实现 EMD-CIIT，本文采用小波除噪的方法对IMF1降噪，可以看到其对高频信号中的除噪效果并不理想，这是由于在构造同原信号有相同信噪比的序列时，如果IMF1中含有有用信息，经过多次迭代，将含有小幅度有用信息的值叠加到高阶的IMF上，造成信号的变形，所以其滤波效果同样依赖于第1阶IMF除噪时小波参数的选取，有很大的局限性。本文算法完全依赖于信号本身，不需要其他滤波方法的辅助，所以其自适应较好，可以看到其对不同频率的信号均有良好的处理效果。

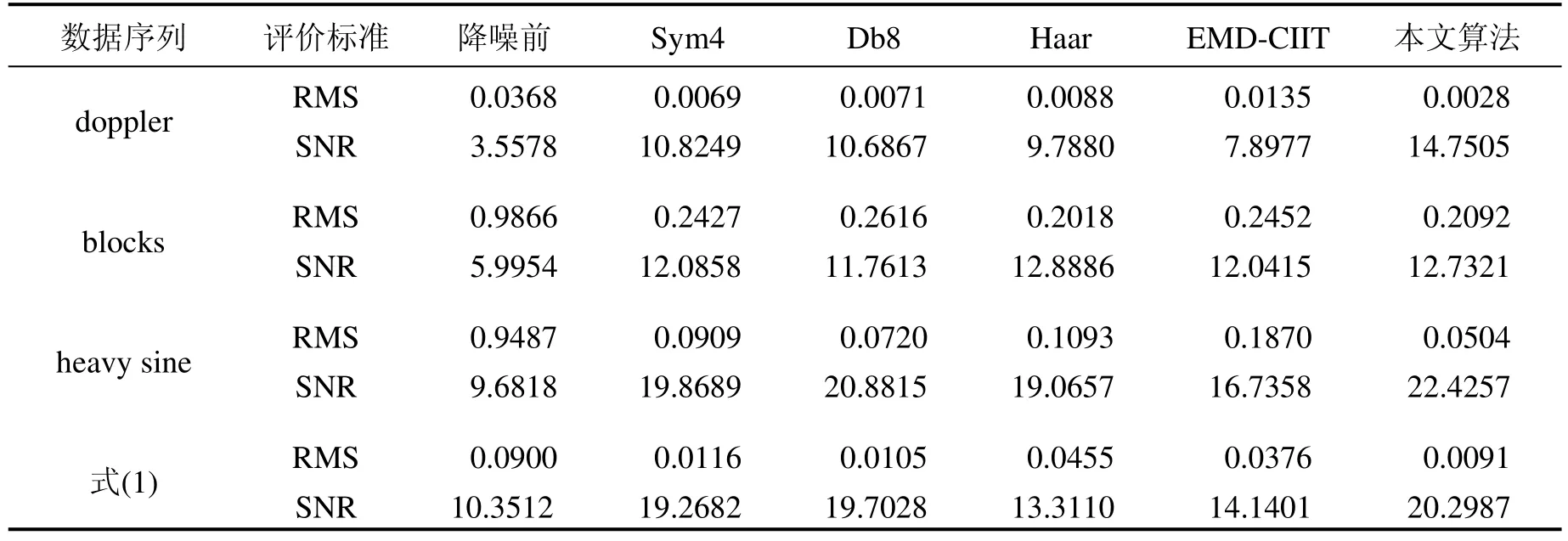
表1 仿真数据的降噪效果Tab.1 Results of de-noising effect of simulated data

4.2 GPS信号仿真

本文使用的GPS数据采样周期为1 s，数据长度600个历元，整个采集过程9颗卫星可见(PRNs 1,6,10,16,17,21,22,26,30)，选择仰角为的PRN-1作为参考卫星。图4为短基线模式下多接收机系统差分模型测量的基线误差，三组数据分别为三个从接收机与主接收机的基线误差，由于是短基线测量，可以发现三组基线误差数据的趋势项基本一致，接收机的多径误差非常接近，可以认为该误差主要为多径误差和热噪声。分别采用小波降噪、EMD-CIIT以及本文算法对基线误差进行处理，其中小波降噪选择 sym4小波，分解层次为3，其余两种方法的参数和上文一致，图5显示了应用三种除噪方法提取信号中多径误差的结果,蓝实线为原始误差数据，点划线表示 EMD-CIIT，虚线为DWT，实黑线为本文算法。图中方框覆盖的部分被放大至图形下方显示，可以发现EMD-CIIT能滤除一些高频噪声，但是其效果不如小波变换和本文算法，本文算法在信号的高频处不仅能保留小幅度的信号波动信息，还能尽可能的滤除高频噪声，较小波变换能更好的保留信号的小幅波动信息，降噪后的基线误差即为多径误差，可以用来补偿GPS测量数据。

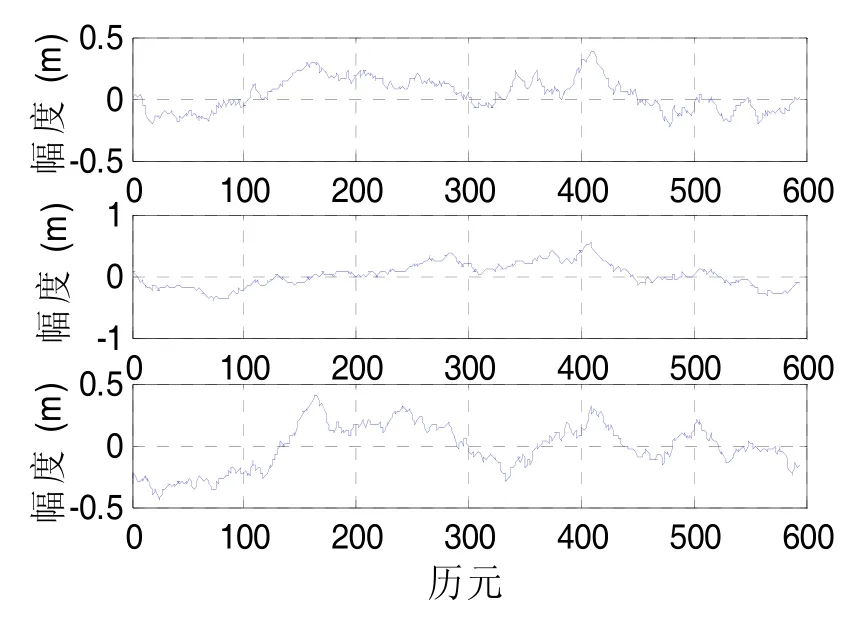
图4 多接收机测量系统基线误差Fig.4 Baseline errors of multi-receiver system

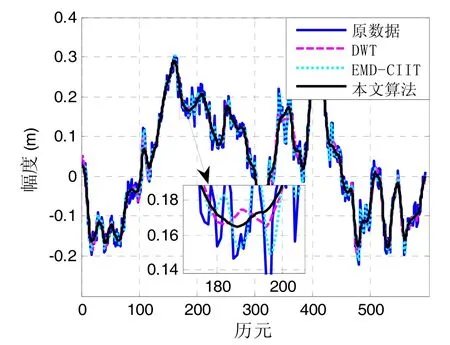
图5 基线误差的除噪效果Fig.5 De-noising effects of baseline errors

5 总 结

本文通过研究噪声在EMD分解中的传播特性，提出利用噪声辅助数据分析方法将信号中的噪声压缩至低阶IMF中，提高了噪声与有用信息的辨识度。由于短基线 GPS双差分测量结果中多径信号主要是低频信号，低频信号降噪时，EMD部分重构滤波方法也能获得很好的效果，所以在改善了EMD分解的噪声分布后，结合区间阈值滤波和部分重构法实现了一种自适应EMD阈值降噪方法。为了消除噪声位置对滤波结果的影响，构造了多个与原信号有相同信噪比的序列，然后采用多次滤波运算并求滤波结果均值的方法消除EMD分解的位置敏感性误差。模拟数据和GPS数据仿真验证了本文算法的有效性，本文算法也可用于其它非平稳信号的除噪。

[1]Weill L R.Conquer multipath:The GPS accuracy battle,innovation[J].GPS World,1997,8(4):59-66.

[2]Liu Lilong,Wen Hongyan,Liu Bin.Mitigation of systematic errors of GPS positioning based on wavelet denoise[C]//2010 Second WRI Global Congress on Intelligent Systems.2010:253-255.

[3]Zhong P,Ding X L,Zheng D W.Adaptive wavelet transform based on cross-validation method and its application to GPS multipath mitigation[J].GPS Solut,2008,12:109-117.

[4]Mosavi M R,Azarbad M R.Multipath error mitigation based on wavelet transform in L1 GPS receivers for kinematic applications[J].Int.J.Electron.Commun.(AEU).2013,67:875- 884.

[5]Chen Jun,Shang Xiaodong.GPS multipath effect mitigation algorithm based on empirical mode decomposition[J].Earth and Space,2010:2395- 2404.

[6]Kopsinis Y,McLaughlin S.Development of EMD- based denoising methods inspired by wavelet thresholding [J].Transactions on Signal Processing,2009,57(4):1351-1362.

[7]李豹，许江宁，曹可劲，等.北斗二代导航信号抗多径性能分析与仿真[J].中国惯性技术学报，2012，20(3)：339-342.LI Bao,XU Jiang-ning,CAO Ke-jin,et al.Analysis and simulation on anti-multipath performance of Beidou2 navigation[J].Journal of Chinese Inertial Technology,2012,20(3):339-342.

[8]宋超，李景森，皮寿熹.GPS局域增强系统基准站多路径抑制消除技术[J].中国惯性技术学报，2010，18(2)：204-208.SONG Chao,LI Jing-sen,PI Shou-xi.Technique of multipath- free to GPS local area augmentation system [J].Journal of Chinese Inertial Technology,2010,18(2):204-208.

[9]Hassani H.Singular spectrum analysis based on the minimum variance estimator[J].Nonlinear Analysis:Real World Application,2010(11):2065- 2077.

[10]Wu Zhaohua,Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[11]胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断，2011，31(4)：429-434.HU Ai-jun,SUN Jing-jing,XIANG Ling.Mode Mixing in empirical mode decomposition[J].Journal of Vibration,Measurement &Diagnosis,2011,31(4):429-434.

[12]Flandrin P,GonÇalvès P,Rilling G.Empirical mode decomposition as a filter bank[J].IEEE Signal Process.Lett.,2004,11(2):112-114.

Multipath mitigation of GPS signal based on improved EMD algorithm

CUI Bing-bo,CHEN Xi-yuan
(School of Instrument Science and Engineering,Southeast University,Nanjing 210096,China)

An improved filter method based on EMD is proposed to mitigate the multipath effects in short baseline double-difference GPS observation.Noise-assist data analysis is adopted to compress the noise for low-order intrinsic mode function (IMF) after analyzing the propagation of noise in EMD.Signal-to-noise ratio (SNR) of the higher order IMF is increased which improves the accuracy of the EMD decomposition.A new threshold de-noising method is developed based on the proposed EMD algorithm.By altering in a random way the position of the samples of the first IMF,different noise versions of the original signal are obtained,and the position sensitive error of EMD is mitigated by averaging the multiple de-noising results.A comparative evaluation is made on simulation signals among wavelet de-noising method,conventional EMD threshold de-noising and our proposed method,and the results show that our proposed method outperforms the other two.At last,the method is applied in short baseline double difference GPS observation to separate the multipath errors and the results show that the new method is effective.

EMD;multipath effect;GPS;wavelet de-noising

U666.1

A

1005-6734(2014)03-0346-06

10.13695/j.cnki.12-1222/o3.2014.03.013

2014-01-20；

2014-04-21

国家自然科学基金（51375087，50975049）；高等学校博士学科点专项科研基金资助课题（20110092110039）,海洋公益性行业科研专项经费项目（201205035-09）

崔冰波（1986—），男，博士研究生，从事卫星导航、组合导航研究。E-mail：cuibingbo@163.com

联 系 人：陈熙源（1962—），男，教授，博士生导师。E-mail：chxiyuan@seu.edu.cn