非负矩阵Hadamard积谱半径的界值*
2014-07-19李华
李 华
(河南城建学院数理学院,河南 平顶山 467036)
非负矩阵Hadamard积谱半径的界值*
李 华
(河南城建学院数理学院,河南 平顶山 467036)
给出两个n阶非负矩阵A与B的Hadamard积的谱半径上界的一个新估计式, 并且与以往的结果进行比较, 说明所得的估计结果在一定条件下更为精确.
非负矩阵;Hadamard积;谱半径
用A≥0(aij≥0)来表示A是非负矩阵, 用Cn×n(Rn×n)表示n阶复(实)矩阵集,矩阵A=(aij)∈Cn×n的n个特征值λ1,λ2,…,λn组成的集合为矩阵的谱, 记为σ(A). 矩阵A的n个特征值的模的最大值为矩阵的谱半径, 记为ρ(A). 若A为非负矩阵, 则由Perron-Frobenius定理知:ρ(A)∈σ(A),且有非负特征向量与之对应.
对非负矩阵谱半径的研究是矩阵理论的重要研究课题之一,在这方面较为重要的结论有:
引理1[1](Frobenius界值) 如果非负矩阵A=(aij)n×n的行和分别为r1,r2,…,rn, 则有
r≤ρ(A)≤R.
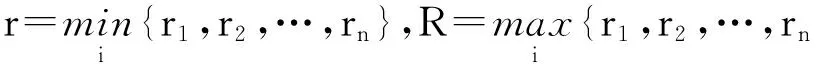
定义1[1]设A=(aij)∈Cn×n,B=(bij)∈Cn×n, 记C=A∘B=(aijbij)为矩阵A与B的Hadamard积.
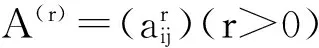
引理 2[3]设a=(a1,a2,…,an)T≥0,b=(b1,b2,…,bn)T≥0, 则有

1 非负矩阵的Hadamard积的谱半径的上界估计
对于ρ(A∘B)的上界估计, 1985年R.A.Horn等在文献[2]中给出了结论:若矩阵A=(aij)∈Rn×n,B=(bij)∈Rn×n,A≥0,B≥0, 则ρ(A∘B)≤ρ(A)ρ(B).
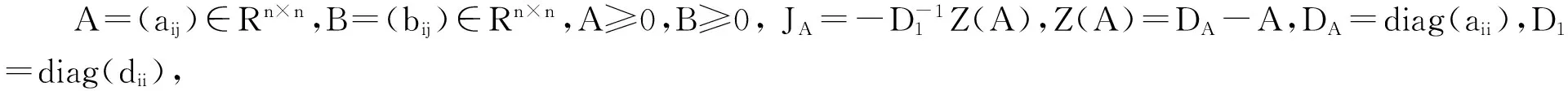

本文在文献[3]~[5]的基础上,给出非负矩阵Hadamard积谱半径上界的新估计式.
定理1 设矩阵A=(aij)∈Rn×n,B=(bij)∈Rn×n,A≥0,B≥0, 则有

其中k=1,2.

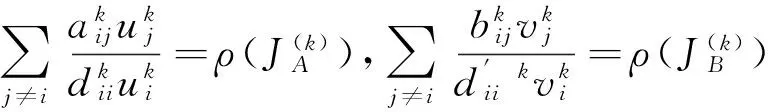
设U=diag(u1,u2,…,un),V=diag(v1,v2,…,vn), W=UV=diag(u1v1,u2v2,…,unvn), 则

由引理2知:
即
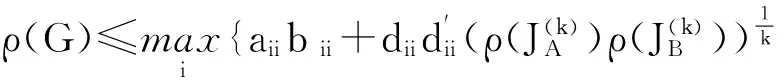
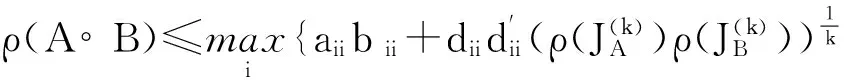
即上式对k=1,2时成立.
若A∘B为可约矩阵, 设D=(dij)为置换矩阵,d12=d23=…=dn-1,n=dn1=1,其余的dij=0,则对任何正实数t,A+tD、B+tD为非负不可约矩阵,用A+tD、B+tD分别代替A、B,令t→0由连续性,可得到相同的结果.
特别: 当∀i∈Naii=0,bii=0,k=1时, 则有ρ(A∘B)≤ρ(JA)ρ(JB).
2 数值例子
在文献[2]中,ρ(A)=4,ρ(B)=2,ρ(A∘B)≤ρ(A)ρ(B)=8.
在定理1中,令k=1,ρ(A∘B)≤4.2248.
实际上,ρ(A∘B)=4. 由此可知, 定理1的结果在一定条件下比以前的结果更为精确.
[1]Frobenius. Uber matrizen aus nicht negativen elementen[M]. Akad.Wiss.(Berlin) S. B. Press, 1912.
[2]Horn R A, Johnson C R. Topics in Matrix Analusis[M]. Cambridge University Press, 1985.
[3]杜琨.矩阵Hadamard积和Fan积的特征值界的界[J].华东师范大学学报, 2008(5):45-50.
[4]Liu Qingbing, Chen Guoliang. On two inequalities for the Hadamard product and the Fan product of matrices[J]. Lin. Alg. Appl., 2009 (431):974-984.
[5]Fang M Z. Bounds on the eigenvalues of the Hadamard product and the Fan product of matrices [J]. Lin. Alg. Appl., 2007(425):7-15.
New bounds on Perron root of Hadamard product of nonnegative matrices
LI Hua
(SchoolofMathematicalandPhysicalScience,HenanUniversityofUrbanConstruction,Pingdingshan467036,China)
A new type upper bound of spectral radius of Hadamard product for nonnegative matrices is given. We comparde the new bounds with the previous results, which shows that the bounds are better than the previous results.
nonnegative matrices; Hadamard product; spectral radius
河南省科技计划项目(112300410191);河南省教育厅自然科学基金项目(13B520945).
2013-03-16
李 华(1978-),女,河南南阳人,河南城建学院数理学院讲师。
1674-7046(2014)01-0085-03
O151.21
A
