平行映射下保测地线的曲面
2014-07-19苏农刘玲
苏农,刘玲
(北京信息科技大学理学院数学系,北京100192)
平行映射下保测地线的曲面
苏农,刘玲
(北京信息科技大学理学院数学系,北京100192)
利用古典微分几何方法,讨论了在平行映射下测地线不变的曲面若干局部性质;研究了该类曲面的测地坐标系,并最终得出满足该条件的曲面只有三类.
平行曲面;测地线;测地极坐标;测地平行坐标系
1 引言
文献[1]通过计算证明了如果曲面上的测地线在平行映射下仍为测地线,则该测地线必为平面曲线、直线或空间贝特朗曲线.文中作者提出了更进一步的问题:曲面M的所有测地线在平行映射下的像都是的测地线,那么M是否只可能是平面、圆柱面、球面之一?本文利用曲面理论,研究了在平行映射下测地线保持不变的曲面的局部测地坐标系的一些特性,最终证明了以下结果.
定理1.1设M为连通可定向的光滑曲面,σ:M→为平行映射.如果对M上的任意测地线Γ,均有=σ(Γ)是上的测地线,则M在局部上只能为平面、球面或圆柱面.
2 预备知识
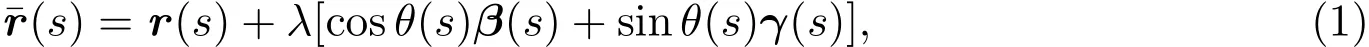
命题2.1两光滑曲线平行的充要条件是它们的公垂线构成的法线曲面是可展的.
命题2.2[2]设是Γ的平行曲线,则在与Γ对应点处有相同的主法向量,且在对应点处的曲率和挠率满足
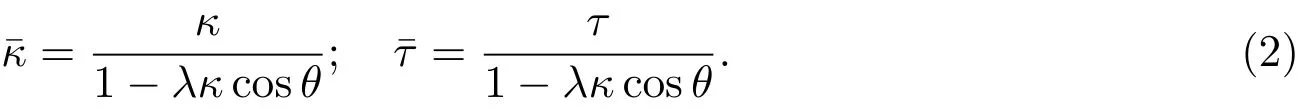
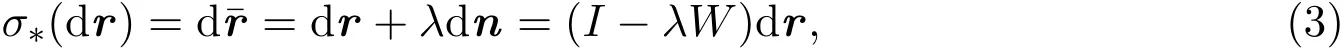
其中W是M上于p点的Weingarten映射,I是恒等映射.显然σ∗自共轭,且其特征方向与W的特征方向相同.如果dr是p点的主方向,则d∥dr.反之,如d∥dr,则dr是p点的主方向,同时d是点的主方向.因此有
命题2.3[3]dr是M上p点的主方向的充要条件是对M的任意平行曲面均有d∥dr,即主方向是σ∗不变的.
设
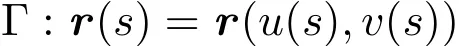
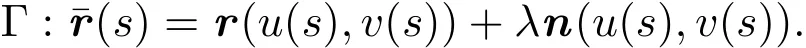
由命题2.1以及Rodriques定理得
命题2.4[3]曲面M上的曲线Γ为曲率线的充要条件是其在M的平行曲面上的对应曲线与之平行.
命题2.5[3]曲线Γ为曲面M上的曲率线的充要条件是其平行曲面上的对应曲线也是曲率线,即曲率线是σ不变的,且σ将脐点映到脐点.
命题2.6[3]设M是光滑曲面,σ:M→是平行映射,κ1,κ2及,分别是p∈M及=σ(p)∈处的主曲率,则
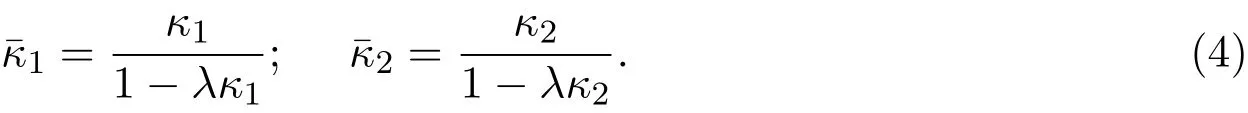
命题2.7[4]设曲面M:r=r(u,v)的参数曲线为正交曲率线,κ1,κ2是主曲率,则有Codazzi方程:
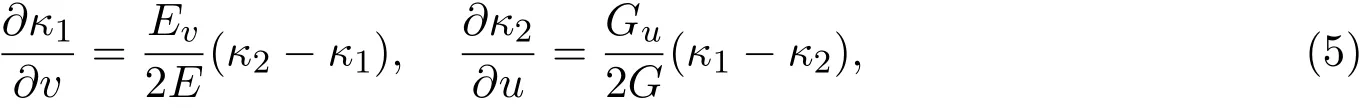
其中E=ru·ru,G=rv·rv是曲面的第一基本量.
3 充要条件
设M:r=r(u,v)是三维欧式空间中的光滑曲面,σ:M→是平行映射.则有
定理3.1如果Γ是M上的测地线,则=σ(Γ)是上测地线的充要条件是:Γ与夹角为定值.
证明于M和上取一阶标架场(r;e1,e2,e3)以及(),使得ei=(i=1,2)为切向量场,e3=为法向量场.设s,分别是为Γ和的弧长参数,Γ和与e1夹角分别是θ,.由于Γ是测地线,因此

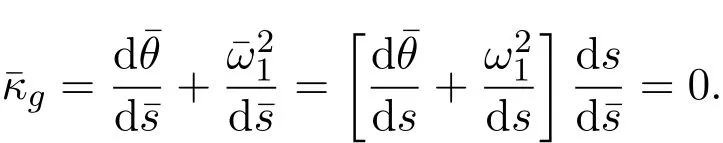

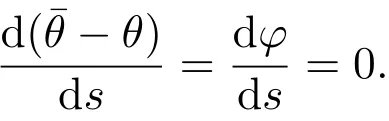
推论3.1设p0∈M,v0∈Tp0M是p0∈M点的主方向,|v0|=1.Γ是M上通过p0点,以v0为切向量的测地线,如果其在M的平行曲面上的对应曲线也是测地线,则Γ是平面曲线.
证明设s是为Γ的弧长参数,p0点对应参数为s0,φ是Γ和的夹角.由命题2.3和定理3.1可知φ满足所以,φ≡0,即Γ和是相互平行的曲线.根据命题2.4知Γ是M上的曲率线.

设(r(s);α(s),β(s),γ(s))(s是弧长参数)是Γ的Frenet标架,其曲率、挠率和法曲率分别为κ,τ和κn.由于Γ是测地线,所以
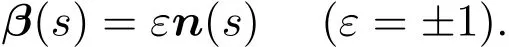
而Γ又是曲率线,因此所以,τ=0,即Γ是平面曲线.

注3.1推论3.1说明,如果Γ和=σ(Γ)同为测地线,且Γ上有一点的切向量为曲面在该点的主方向,则Γ必是曲率线,所以是平面曲线.
注3.2在推论3.1的条件下,经过Γ上每一点,由Γ切方向决定的法截线、法截面重合;曲线Γ上每一点处与Γ正交的主方向都正交于公共的法截面,因此是相互平行的.
4 测地坐标系及定理的证明
设M是光滑曲面,p∈M.由曲面论可知,切平面TpM上的极坐标系(s,θ)确定了曲面在p点的测地极坐标系(这里0 引理4.1[4](Gauss引理)Σ与Σ′是彼此正交的曲线族. 定理4.1设M是光滑曲面,p∈M是脐点,σ:M→为平行映射.如果对任意从p出发的测地线Γ,均有=σ(Γ)是上的测地线,则M为旋转曲面,Σ是经线族,Σ′是纬线族, p点的法线是旋转轴. 证明设(s,θ)为p点的测地极坐标,曲面的位置向量为r(s,θ),p点位置向量为r0,对应参数s=0,p点处的法向量为n0.根据推论3.1和注3.1,可知 因此, 所以,M是s-曲线绕p点的法线的旋转曲面. 注4.1由定理4.1易知,Σ,Σ′实际上是曲面在p点的局部正交曲率线网,而s是弧长参数,因此曲面的第一基本形式为 设s-曲线的主曲率为κ1,则由命题2.7得 设p∈M,v0∈TpM是p点处的单位切向量,Γ是M上通过p点,以v0为切向量的测地线,其弧长参数为v.令T为曲面上沿Γ的光滑切向量场且与Γ正交,|T|=1.记从Γ上v点出发,以Tv为切向量的测地线族为Σ,则Σ覆盖了Γ的某一单侧邻域U,取与Σ正交的曲线族Σ′,这样Σ和Σ′构成U内的测地平行坐标系.设Σ和Σ′分别由u-(u是弧长参数)和v-曲线构成,Γ对应参数u=0,则曲面第一基本形式满足 利用推论3.1以及(2),(5)式,易证 定理4.2设M是光滑曲面,p∈M,σ:M→为平行映射.Γ是经过p,在该点的切向量为p主方向的测地线,Σ和Σ′是Γ的单侧邻域U内的测地平行坐标系.如果=σ(Γ)是上的测地线,σ(Σ)是覆盖了σ(Γ)单侧邻域内的测地线族,则Σ,Σ′都是平面曲线族,其中Σ′是相互平行的曲线族,Σ族中曲线的主曲率与v无关,Σ,Σ′构成U内的正交曲率线网.特别地,如果Γ是直线,则曲面片U是一般柱面或平面. 引理4.2[5]如果M是处处为脐点的连通曲面,则M必为球面或平面. 定理1.1的证明:设p∈M,Γ1,Γ2是从p出发且在该点的切向量为p点相互正交主方向的测地线,v,u分别为它们的弧长参数,p点对应u=0,v=0.令Σ1和Σ′1是Γ1的单侧邻域U∩1内的测地平行坐标系,Σ2和Σ′2是Γ2的单侧邻域U2内的测地平行坐标系.考虑U=U1U2/=∅内的两参数曲线族Σ1,Σ2,由定理4.2可知,他们既是测地线族,也同时为曲率线族. 1.如果Σ1,Σ2非正交,则U内存在非正交曲率线网,所以U内处处是脐点,根据引理4.2,得U是一片球面或平面. 2.如果Σ1,Σ2正交,则曲面的第一基本形式为: 由于u-曲线和v-曲线都是测地线,利用Liouville公式可得Ev=0,Gu=0,所以Gauss曲率K≡0,即该曲面片是可展的,由定理4.2可知曲面片U是一般柱面或平面. 设Γ:r=r(s)是一般柱面M上的测地线,s为其弧长参数,Γ与M的直母线夹角为θ,母线方向为v0,|v0|=1,(r(s);α(s),β(s),γ(s))是Γ的Frenet标架,κ,τ为其曲率和挠率.于是有,β(s)=±n(s),所以, 因此, 设Γ是正螺线,根据正螺线的特性知, 是常数[3].将β(s)…v0=0两边求导得 又因为 所以τ/=0,即Γ是空间挠曲线.如果Γ是空间Bertrand曲线,于是存在常数λ/=0及µ,使得 将(11)式代入(12)式得到κ,τ都是常数,因此Γ是圆柱螺线,M必为圆柱面. 更进一步问题设Mn为中定向连通超曲面,σ:M→为平行映射.如果对M上的任意测地线Γ,=σ(Γ)都是上的测地线,那么曲面片M是否必为 之一? [1]吴报强.曲面的平行曲面[J].徐州师范大学学报,1999,17(4):1-4. [2]苏农.欧式空间的平行曲线及其应用[J].沈阳师范大学学报,2009,27(1):24-27. [3]何源川.欧式空间中的相互平行子流形[J].美大学学报,1996,1(1):26-31. [4]陈维桓.微分几何[M].北京:北京大学出版社,2006. [5]陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社,1999. Surface which keep geodesics corresponding under parallel mapping Su Nong,Liu Ling By the classical theory of di ff erential geometry,we get some local properties of surfaces which keep geodesics corresponding under parallel mapping.Moreover,we discuss the geodesic coordinates of these kind of surfaces and fi nally proved that only three kins of surfaces satisfy the precondition. parallel surface,geodesics,geodesic polar coordinates,geodesic parallel coordinates O186.11 A 1008-5513(2014)03-0280-06 10.3969/j.issn.1008-5513.2014.03.009 2014-01-19. 北京市教委科技面上项目(KM201211232017);北京市委组织部优秀人才培养资助项目(2012D005007000005). 苏农(1966-),硕士,研究方向:微分几何. 2010 MSC:53A04,53A05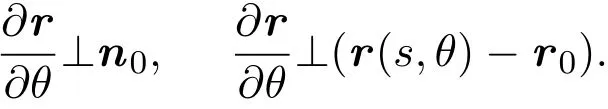
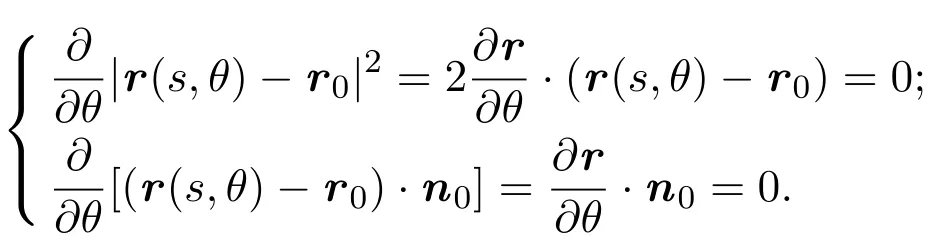

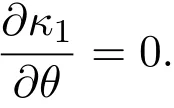
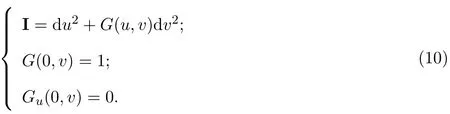
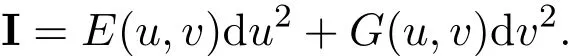
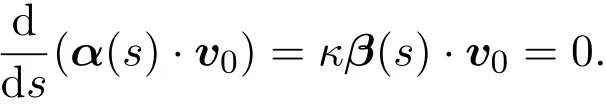
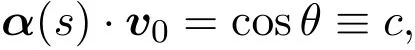

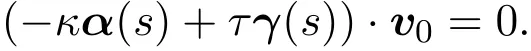


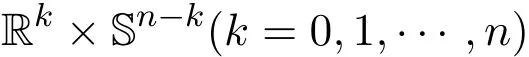
(Department of Mathematics,Beijing Information Science and Technology University,Beijing100192,China)
