一种自适应预处理的BiCRSTAB算法
2014-07-19张晋李春光景何仿
张晋, 李春光, 景何仿
(1.北方民族大学数学与科学学院,宁夏 银川 750021; 2.北方民族大学数值计算与工程应用研究所,宁夏 银川 750021)
一种自适应预处理的BiCRSTAB算法
张晋1, 李春光2, 景何仿2
(1.北方民族大学数学与科学学院,宁夏 银川 750021; 2.北方民族大学数值计算与工程应用研究所,宁夏 银川 750021)
提出一种自适应预处理的BiCRSTAB方法,该预处理可以看作一个隐式构造多项式的预处理方法,由BiCRSTAB算法中嵌入几步GMRES迭代自适应构造而成.数值算例表明,该方法能有效减少迭代步数,从而减少计算过程中的贮存量和运算量.
线性方程组;自适应预处理;BiCRSTAB算法;GMRES算法
1 引言
但是,对于实际应用中某些复杂的问题,BiCRSTAB方法仍然存在收敛速度缓慢或是收敛行为不规则的现象,为了克服这些问题,本文后面将提出一种自适应预处理的BiCRSTAB方法,该方法可以看作一种隐式的构造多项式预处理方法,它由BiCRSTAB算法中嵌入几步GMRES[1]迭代自适应构造而成.能有效地减少迭代步数,降低存储量和运算量,运算时间也相应的减少.
2 一种自适应预处理的BiCRSTAB算法
数值实验表明BiCRSTAB算法收敛速度比BiCR算法快而且更加稳定,然而在一些实际问题应用中,BiCRSTAB算法收敛得很慢甚至会停滞.因此如何选择适当的预条件子成为BiCRSTAB算法高效求解这类问题的关键.下面给出原始预条件的BiCRSTAB算法:
算法 1原始预条件的BiCRSTAB算法
1.对于给定的x0,计算r0=b−Ax0;
2.令p0=r0,q0=AM−1r0,=q0,=;
3.For j=1,2,···,直到收敛
10.rj+1=sj−ωjtj;
14.pj+1=rj+1+βj(pj−ωjqj);
17.End.
算法1的每一步迭代都需要计算M−1rj和M−1qj,也就是说,每一步迭代都需要计算M−1v这样的形式,预条件的关键就是使AM−1近似于一个单位矩阵,即

可以得到M−1v近似于A−1v,而在某种程度上来讲M 应与A近似.
下面给出一个新的BiCRSTAB算法预处理矩阵M的隐式构造过程,亦即对任一给定的n维向量z,当需要计算M−1v=z时,都转化为用k步GMRES求解方程组Mv=z,其中k常取2或3,m的值由具体问题来确定的.根据上述过程,可用迭代结果M−1z作为近似值,其中初始向量v0取为零向量,算法中的隐式构造预处理实际是一个多项式预处理,证明见文献 [3].
算法 2一种自适应预处理的BiCRSTAB算法
1.对于给定的x0,计算r0=b−Ax0,选择=P(A)r0;
3.For j=1,2,···,直到收敛
5.αj=
6.sj=rj−αjqj;
8.tj=
9.ωj=
10.xj+1=
11.rj+1=sj−ωjtj;
15.βj=
16.pj+1=rj+1+βj(pj−ωjqj);
18.qj+1=
19.End.
3 数值算例
下面给出几个数值算例来比较原始的BiCRSTAB算法,BiCR算法,以及自适应预条件的BiCRSTAB算法的执行结果.为了使数值结果便于重复,这里具体给出各参数的值,而不考虑算法的执行细节.选取右端向量b使得方程组Ax=b的精确解为xT=(1,1,···,1),预初始估计值为=(0,0,···,0).
例 1本算例中的系数矩阵A取自文献[4],具有如下形式:

取求解精度Tol=10−8,矩阵阶数n=2000,当α=20000时,A是典型的非对称矩阵,当α=1.1时,系数矩阵A接近对称矩阵,三种方法得到迭代收敛效果如图1,图2所示.

图1 算例1的数值结果(α=20000)

图2 算例1的数值结果(α=1.1)
例 2本算例中的系数矩阵A=CDC−1,C为n阶的随机矩阵,
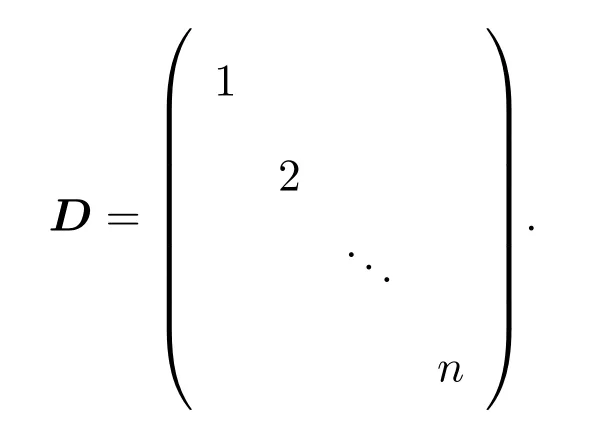
当Tol=10−8,n=2000时,得到迭代收敛效果如图3所示.

图3 算例2的数值结果
例 3本算例的系数矩阵A取自文献[5],A=SBS−1,

当Tol=10−8,n=2000时,得到迭代收敛效果如图4所示.

图4 算例3的数值结果
例 4[6]考虑如下二阶椭圆形偏微分方程

其中,S={(x,y)∈R2,0 我们用中心差分离散方程,把区域S划分成网格尺寸为h=1/l+1的(l+2)×(l+2)个均匀正方形网格,网格点为si=ih,tj=jh,0≤i,j≤l+1.整个方程被离散成五点格式,把网格点按自然次序排序得l2×l2块三对角矩阵: 其中,γ=p1h,β=p2h,σ=p3h,线性系统右端的元素为h2f(si,tj),为简单起见以下算例右端向量取b=sum(A,2),以下取l=50,p1=25,p2=50,p3=30得到的结果如图5所示. 图5 算例4的数值结果 下面给出pBiCRSTAB算法,BiCRSTAB算法以及BiCR算法三类算法的迭代次数及计算时间比较,见表1,表2. 本文提出一种求解大型系数线性方程组的自适应BiCRSTAB算法,在每一步外迭代中的预处理子是不断变化的.数值算例表明,新算法与原始的BiCRSTAB算法相比较,迭代次数减少同时收敛速度加快. 表1 各方法的迭代次数比较 表2 各方法的CPU时间比较 [1]Saad Y.Iterative Methods for Sparse Linear Systems[M].Boston:PW Publishing Company,1996. [2]Abe K,Sleijpen G L G.BiCR variants of the hybrid BiCG methods for solving linear systems with nonsymmetric matrices[J].Comput.Appl.Math.,2010,234:985-994. [3]Cao H Y,Li X W.CGS/GMRES(k):An adaptive preconditioned CGS algorithm for nonsymmetric linear systems[J].Numer.Math.,1998,7:145-158. [4]Niu Q,Lu L Z,Wang R R.A modif i ed GMRES method for solving large nonsymmetric linear systems[J].高等学校计算数学学报,2005,27:193-199. [5]Sadok H.CMRH:A new method for solving nonsymmetric linear systems based on the Hessenberg reduction algorithm[J].Numerical Algorithm,1999,20:303-321. [6]全中,向淑晃.基于GMRES的多项式预处理广义极小残差法[J].计算数学,2006,28(4):365-376. An adaptive preconditioned BiCRSTAB algorithm for linear Zhang Jin1,Li ChunGuang2,Jin HeFang2 An adaptive preconditioned BiCRSTAB is presnted,which which is combined with an polynomial preconditioner constructed implicitly,and several steps of GMRES are inserted in BiCRSTAB algorithm.Numerical experiments illustrate this method can reduce the iterative steps and computation time ef f ectively. linear systems,adaptive preconditioning,BiCRSTAB,GMRES O241.6 A 1008-5513(2014)02-0195-06 10.3969/j.issn.1008-5513.2014.02.011 2013-12-26. 国家自然科学基金重大研究计划培育项目(91230111);宁夏自然科学基金(NZ13086);国家自然科学基金(11361002). 张晋(1987-),硕士生,研究方向:数值代数. 李春光(1964-),教授,博士生导师,研究方向:流体力学与计算数学. 2010 MSC:65F10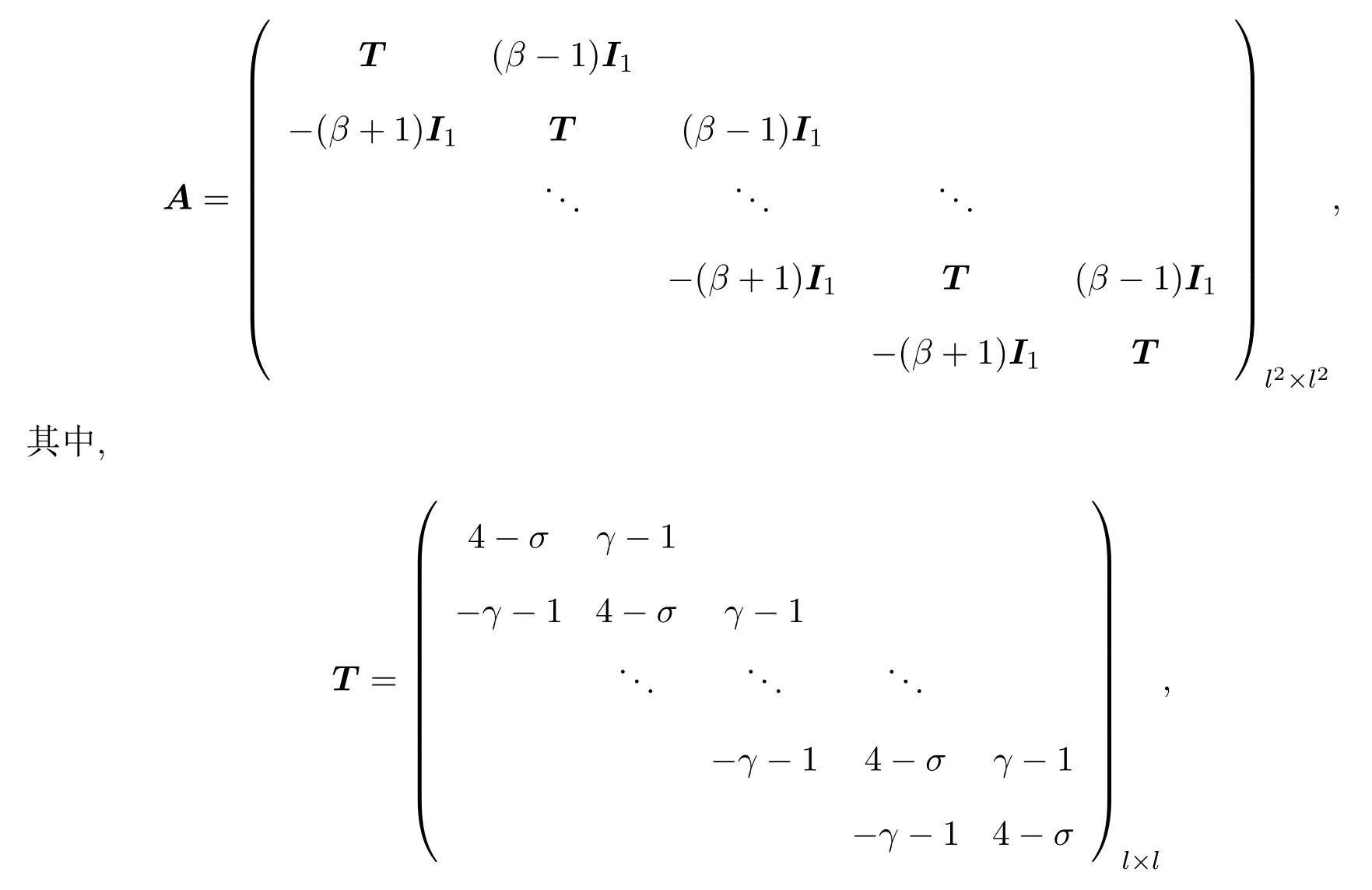

4 结论


systems
(1.School of Mathematics and Information Science,Beifang University of Nationnalities, Yinchuan 750021,China; 2.Institute of Numerical Computation and Engineering Application,Beifang University of Nationnalities, Yinchuan 750021,China)
