非可微多目标优化问题的高阶逆对偶定理

高英

(重庆师范大学数学学院,重庆 400047)

非可微多目标优化问题的高阶逆对偶定理

高英

(重庆师范大学数学学院,重庆 400047)

在锥约束非可微多目标优化问题Mond-Weir型高阶弱对偶定理的基础上,利用Fritz-John型必要条件,在没有任何约束品性条件下给出了逆对偶定理.最后,考虑了特殊情况,研究了单目标情况下对偶问题的逆对偶定理.

非可微多目标优化,高阶对偶,逆对偶定理

1 引言

设f:Rn→R和g:Rn→Rm二阶可微,B是n×n半正定对称矩阵.文献[1]首次建立了如下非可微数学规划问题的一阶对偶模型,并证明了对偶定理.

文献[2]首次提出非线性规划问题的二阶和高阶对偶模型,并在一定条件下建立了对偶定理.文献[3-4]在一阶对偶模型的基础上考虑了另一种二阶和高阶对偶模型,并在更简单的条件下给出了对偶定理.随后,诸多学者研究非线性规划问题的二阶和高阶对偶问题,得到了丰硕的成果[5-17].文献[5]考虑了问题(P)的一阶和二阶对偶模型,在一定广义凸性条件下建立了弱对偶、强对偶和逆对偶定理.文献[6]将文献[5]中的结果推广到高阶对偶问题的研究,在高阶广义凸性条件下给出了对偶定理.文献[7]研究了非可微多目标优化问题的Mangasarian型和Mond-Weir型对偶模型,在更广的广义凸性假设研究了对偶定理.最近,文献[8]利用紧凸集的支撑函数代替问题(P)中的(xTBx)得到了更一般的非线性规划模型,研究了其一阶和二阶对偶问题.

文献[9]利用Fritz John型必要条件在没有任何约束品性条件下建立了可微非线性规划问题的逆对偶定理,并称之为Huard型逆对偶定理.随后,诸多学者在此基础上研究了一阶、二阶和高阶逆对偶定理[12-16].最近,文献[10]考虑了非可微多目标优问题的统一高阶对偶模型,建立了弱对偶、强对偶和严格逆对偶定理.文献[11]研究了多目标优化问题的弱对偶和强对偶定理.但在文献[10-11]中都没有考虑到文献[9]提出的逆对偶定理.针对该情况,本文利用Fritz John型必要条件,在没有任何约束品性条件下建立一类非可微多目标优化问题的逆对偶定理.

2 预备知识

设Rn是n维欧式空间,是非负象限.对x,y∈Rn给出以下符号:

Φ(x)是定义在 Rn上的二阶连续可微实值函数,h(x,y)是定义在 Rn×Rm上的函数,∇xΦ()表示函数Φ在点的梯度向量,∇xxΦ()表示在点的Hessian矩阵,∇xh(,)表示函数 h关于变量 x在点 (,)处的梯度向量,∇xxh(,)表示关于变量 x在点 (,)处的Hessian矩阵.同理,还有以下符号:∇yh(,),∇xyh(,),∇yyh(,).为简便起见,∇xΦ()记为∇Φ().设C⊂Rn为紧凸集.集合C的支撑函数定义为:

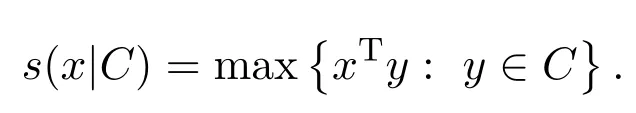
支撑函数是凸函数,故有次微分.即,存在z∈Rn,使得

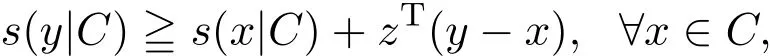
从而s(x|C)的次微分为:

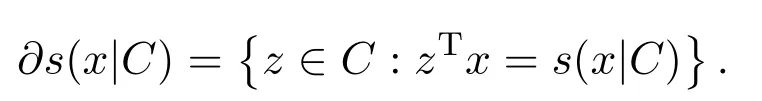
凸集D⊂Rn在点x∈D的法锥定义为:

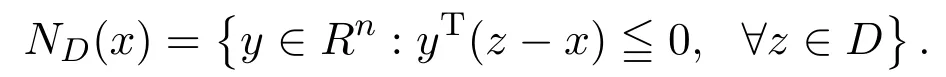
若C是紧凸集,则y∈NC(x)当且仅当s(y|C)=xTy,或等价地x∈∂s(y|C).

锥K⊂Rn的极锥定义为:

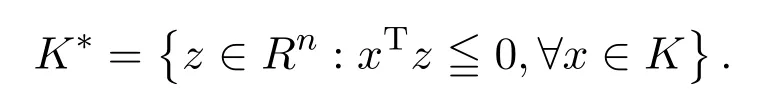
考虑如下多目标优化问题(简称MNP):

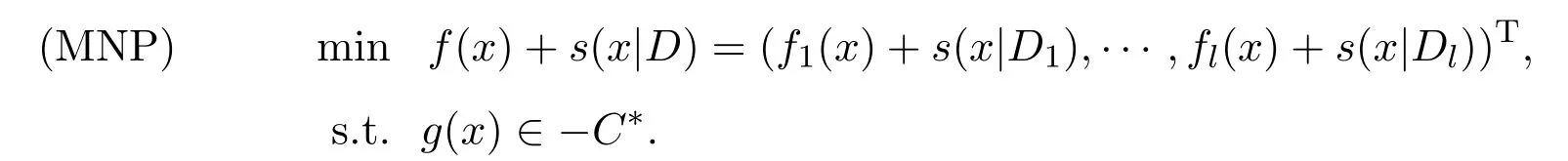
其中,f:Rn→Rl,g:Rn→Rm是二次可微函数,Di是凸紧集,i=1,···,l,C⊂Rm是内部非空的闭凸锥.

(MNP)的可行解集记为 S={x∈Rn:g(x)∈−C∗}.

定义 2.1(i)可行解x0称为问题(MNP)的弱有效解,若不存在x∈S,使得

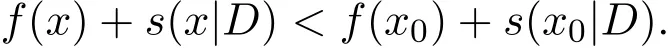
(ii)可行解x0称为问题(MNP)的有效解,若不存在x∈S,使得

3 Mond-Weir型高阶对偶

本节,考虑问题(MNP)的Mond-Weir型高阶对偶模型(MND).

其中,e=(1,···,1)T∈Rl,h(x,y):Rn×Rn→Rl和k(x,y):Rn×Rn→Rm是二阶连续可微的函数,

注 3.1(i)若C=,则问题 (MND)退化为文献[11]中的Mond-Weir型高阶对偶模型.

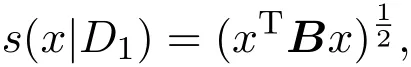
且问题(MNP)和(MND)退化为文献[12]中考虑的问题.

定理 3.1(逆对偶定理) 设是问题(MND)的弱有效解.假设:

证明因是问题 (MND)的弱有效解,由 Fritz-John型必要条件可知,存在α∈Rl,β∈Rn,η∈C∗,ξ∈Rl和θ∈R,使得

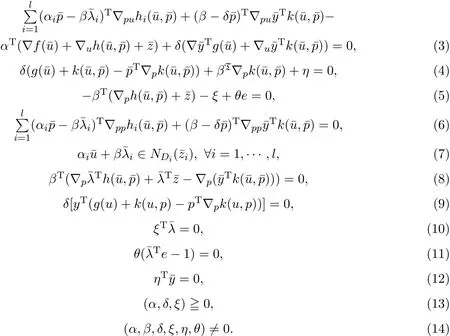
由假设(i)和(6)式,有

因此,(3)式和(4)式分别退化为:

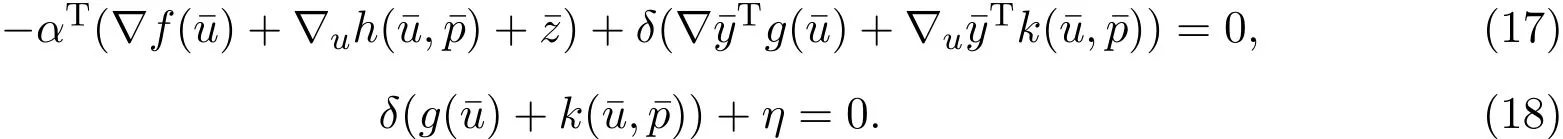
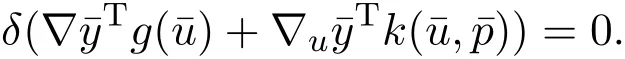
由假设 (ii)得 δ=0.由 (16)式,(4)式和 (5)式得 β=0,θ=0和 η=0. 从而有 (α,β,δ,ξ,η,θ)=0.这与(14)式矛盾.因此,α0.

下面证明 δ/=0.假设δ=0,则(16)式表明β=0.由(15)式得αi=0,i=1,···,l.因为α/=0故=0.由假设(v)可知(17)式退化为:

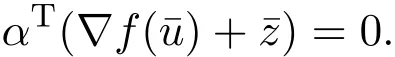
因α/=0,这与假设 (iii)矛盾.从而,δ/=0.

因δ>0,故以上两个等式退化为:

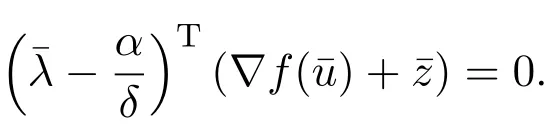
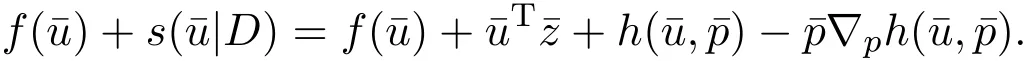
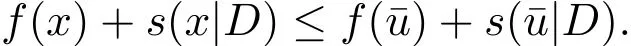
这表明

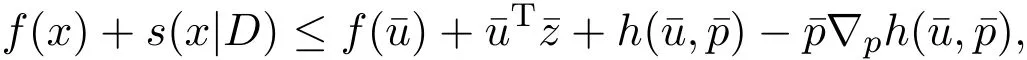
4 特殊情况

本节,考虑单目标情形下的逆对偶定理.

问题(MNP)中取l=1.其对偶问题(MND)退化为问题:

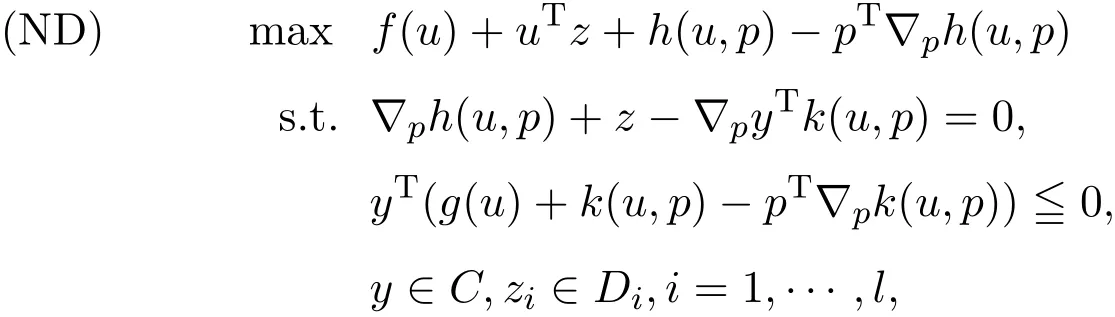
定理 4.1(逆对偶定理)设是问题 (ND))的最优解.假设

证明因是问题(ND)的最优解,故由Fritz-John型必要条件存在α∈R, δ∈R,β∈Rn和η∈C∗使得

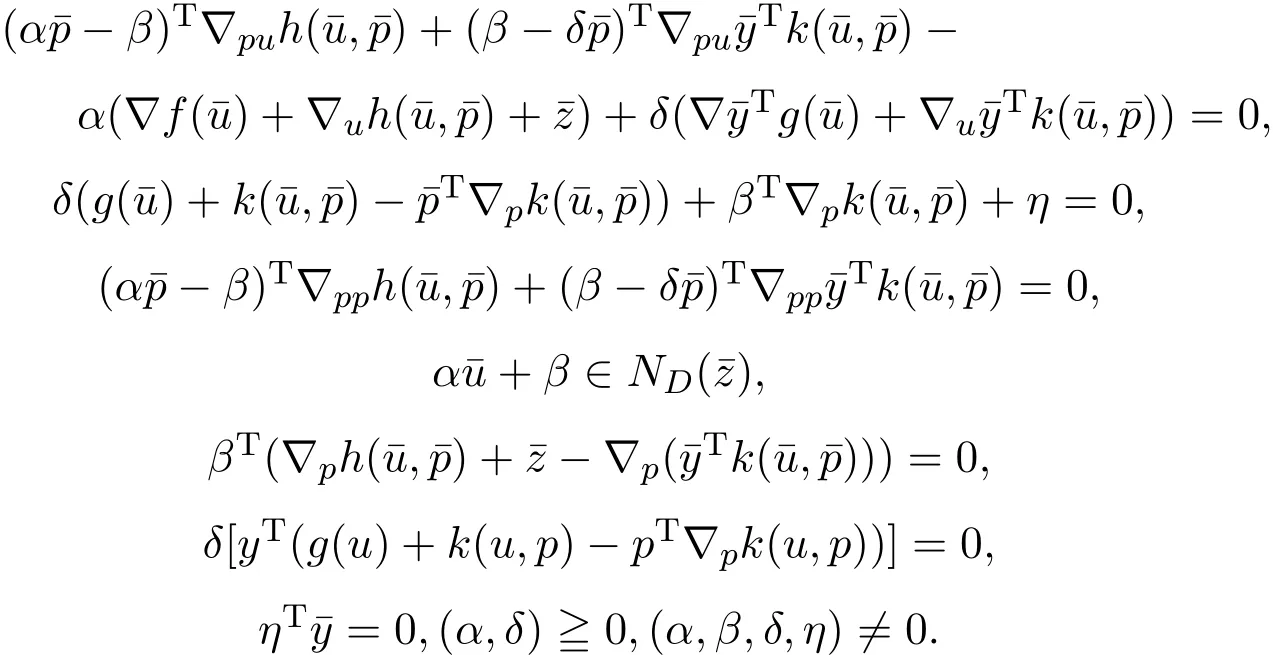
[1]Mond B.A class of nondif f erentiable mathematical programming problems[J].J.Math.Anal.Appl., 1977,46:169-174.

[2]Mangasarian O L.Second and higher order duality in nonlinear programming[J].J.Math.Anal.Appl., 1975,51:607-620.

[3]Mond B,Weir T.Generalized convexity and higher-order duality[J].J.Math.Sci.,1981/1983,16/18:74-94.

[4]Mond B,Zhang J.Higher Order Invexity and Duality in Mathematical Programming[C]//Generalized Convexity,Generalized Monotonicity:Recent Results.Kluwer:Dordrecht,1998.

[5]Zhang J,Mond B.Duality for nondif f erentiable programming problem[J].Bull.Austral.Math.Soc., 1977,55:29-44.

[6]Mishra S K,Rueda N G.Higher-order generalized invexity and duality in nondif f erentiable mathematical programming[J].J.Math.Anal.Appl.,2002,272:496-506.

[7]Jayswal A,Kumar D,Kumar R.Second order duality for nondif f erentiable multiobjective programming problem involving(F,α,ρ,d)-V-type I functions[J].Optim.Lett.,2010,4:211-226.

[8]Yang X M,Yang X Q.On duality for a class of nondif f erentiable programming problems[J].Pacif i c J. Optim.,2008,4:113-124.

[9]Mangasarian O L.Nonlinear Programming[M].New York:McGraw Hill,1969.

[10]Ahmad I.Unif i ed higher-order duality in nondif f erentiable multiobjective programming involing cones[J]. Mathematical and Computer Modelling,2012,55:419-425.

[11]Mishra S K,Wang S Y,Lai K K.Higher-order dualty for a class of nondif f erentiable multiobjective programming problems involving generalized type I and related function[J].J.Syst.Sci.Complex,2011,24:883-891.

[12]Yang X M,Teo K L.A converse duality theorem on higher-order dual models in nondif f erentiable mathematical programming[J].Optim Lett.,2012,6:11-15.

[13]Yang X M,Yang X Q,Teo K L.Converse duality in nonlinear programming with cone constraints[J]. Europ.J.Oper.Res.,2006,170:350-354.

[14]Yang X M,Yang X Q,Teo K L.Huard type second-order converse duality for nonlinear programming[J]. Appl.Math.Lett.,2005,18:205-208.

[15]Yang X M,Zhang P.On second-order converse duality for a nondif f erentiable programming problem[J]. Bull.Austral.Math.Soc.,2005,72:265-270.

[16]Chandra S,Abha.A note on pseudo-invexity and duality in nonlinear programming[J].Europ.J.Oper. Res.,2000,122:161-165.

[17]高英.一类多目标广义分式规划问题的最优性条件和对偶[J].纯粹数学与应用数学,2011,27(4):477-485.

On higher-order converse duality for nondif f erentiable multiobjective programming problems

Gao Ying
(Department of Mathematics,Chongqing Normal University,Chongqing 400047,China)

In this paper,based on the weak duality theorems of Mond-Weir type higher-order dual for nondif f erentiable multiobjective problems with cone constraints,we derive converse duality theorems by using Fritz-John type necessary condition without any constraint qualif i cations.Finally,we consider the special case of the result, and establish converse duality theorem for single objective programming problem with con constraint.

nondif f erentiable multiobjective programming problems,higher-order dual models, converse duality theorems

O221.6

A

1008-5513(2014)02-0136-07

10.3969/j.issn.1008-5513.2014.02.003

2013-09-08.

国家自然科学基金(11201511,11201379);重庆市科委重点实验室专项基金(CSTC,2011KLORSE03).

高英(1982-),博士,副教授,研究方向：最优化.

2010 MSC:90C32,90C46,90C47