应用相位相关法的TDICCD空间相机像移测量方法

胡超 王小勇 郭崇岭

(北京空间机电研究所, 北京 100094)

应用相位相关法的TDICCD空间相机像移测量方法

胡超 王小勇 郭崇岭

(北京空间机电研究所, 北京 100094)

空间相机亚像素精度的像移高精度测量是一项技术难题。文章针对高分辨率TDICCD空间相机的成像特点提出一种直接测量像移的方法，该方法利用高速图像传感器获取图像序列，然后采用基于局部上采样的相位相关法来测定亚像素像移变化曲线。Matlab软件的仿真实验结果表明，该方法对图像噪声和灰度变化有很高的容忍度，其测量精度在图像信噪比高于10 dB时优于0.1个像元。

相位相关；TDICCD相机；高分辨率；像移测量；亚像素

1 引言

目前高分辨率相机多采用推扫成像的时间延迟积分CCD(TDICCD)来实现轻小型化和解决光通量不足的问题[1-2]，以提高图像分辨率。空间相机在曝光时间内，由于卫星在轨高速飞行及卫星平台非稳定因素，都会使影像在像面上发生平移(即像移)，造成图像模糊或几何扭曲，导致相机实际分辨率降低，影响相机图像质量。随着空间相机分辨率指标的提高，对卫星平台稳定性的要求也随之提高，卫星平台非稳态因素造成的像移对相机成像质量的影响越来越重要[1-4]。高精度的像移补偿系统是获取高分辩遥感图像的重要研究方向，要想获得高精度的像移补偿效果，必须先对像移进行精确感知，像移测量成为高分辨率成像的关键技术之一。传统的像移获取方法主要依赖星敏感器、光纤陀螺等姿态测量机构，根据测量的姿态参数和GPS数据计算出像移，然而这种方法精度不高，测量频率有限。解决此问题的方法通常是增加卫星姿态控制的稳定性，并同时减小由动量轮或其它因素引起的卫星振动，但是这将大幅增加卫星的费用、尺寸和质量[4]。目前有一种在空间相机焦面或其他位置安装辅助图像传感器用于获取像移的方法，辅助图像传感器选用小型高速面阵互补金属氧化物半导体(CMOS)或电荷耦合器件(CCD)探测器，利用图像处理算法直接求出图像间的像移[5]。为了防止图像模糊，辅助图像传感器获取图像的曝光时间很短，图像灰度较暗，噪声也比较大，并以很高的帧频输出。因此要实现高精度实时测量，就需要测量计算方法具有高噪声容限和快速处理性能。

根据像移直接测量的思路和TDICCD相机成像特性，本文提出一种将高速图像采集与相位相关法结合的直接测量像移的方法，利用局部上采样来定位亚像素像移，并进行大量对比实验。

2 直接测量像移方法简介

像移测量旨在测量遥感图像实时像移信息，利用测得的像移量进行硬件实时补偿或通过后期图像复原算法，减小和消除像移对图像的影响，提高图像质量。像移测量方法主要包括两个部分：像移测量光路和图像相关算法。本文采用的像移测量方案的光路示意图如图1所示。

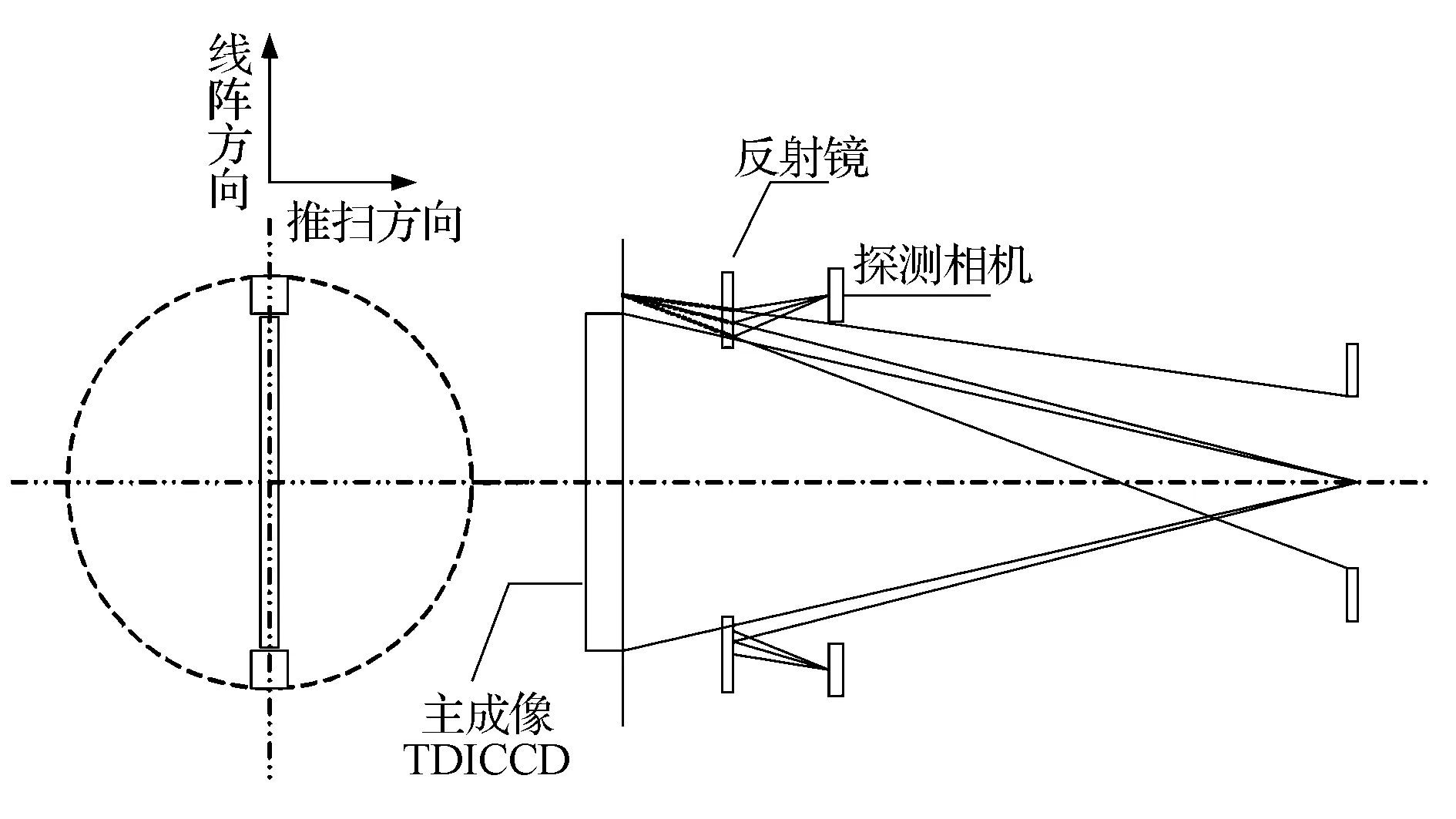
图1 像移测量光路图

探测相机放置在主成像的TDICCD相机的边缘视场处，使得探测相机获取与主相机同光轴的图像，考虑到探测相机的像元数较小，当地面图像为对比度较小的图像时，如海洋、沙漠等，单一的探测相机可能得不到有效的像移信息，因此在像移测量方案中应设置两台探测相机，以保证获取有效的像移信息。在主光学系统成像期间，为准确获取像移信息，探测相机不能出现像移模糊，因而需要探测相机对景物高速采样，采样频率达到成百甚至上千赫兹。这不仅要求探测相机能够高速获取和传输图像序列，同时要求图像传感器具有较高的灵敏度和信噪比。随着图像传感器设计水平、制造工艺技术的飞速发展，越来越多的高灵敏度、高信噪比、高速面阵CCD/CMOS芯片或相机已问世，并且能够应用于航天环境，这也为像移直接测量方法的应用奠定了基础。如德国Mikrotron公司的EoSensCL full高速相机，在1280×1024分辨率下，可以达到500 帧/s的速率，并且可以通过开窗方式减小分辨率来增加帧速率，同时具有感光度2500(ISO2500)的高灵敏度，拥有像素组合牺牲像元空间分辨率、增加感光面积来提高图像曝光量。其他如加拿大达尔萨(DALSA)、德国巴斯勒(Basler)、美国赛普拉斯(Cypress)等公司，都有高速面阵芯片或相机产品。

TDICCD相机成像过程的像移量由多种因素引起，包括速高比变化、姿态稳定度、偏流角，卫星平台颤振等[1,3,6-10]。其像移量可以分解为两个方向：推扫方向和线阵方向，如图1所示。对于推扫方向的像移可保持TDICCD的行转移速度与像移速度同步来消除，而线阵方向像移对TIDCCD的成像质量影响极大，必须进行硬件校正或后期复原。实际上，因为空间飞行的复杂性，尤其是对于高分辨率相机而言，TDICCD的行转移速度(即积分时间)，与推扫速度很难做到完全匹配。TDICCD通过推扫成像，高速面阵相机图像序列间将产生一个卫星推扫方向的前向像移，利用图像相关算法求取主相机像移时应先扣除前向像移。同时因为这部分推扫像移的存在，高速图像间的重合度大大降低，图像相关算法必须适应小重合度图片的像移测量。对于某些图像相关算法，由于图像间像移量过大，图像重合度过小，图像的相关信息不丰富，像移测量的精度将会大大降低，抗噪能力也会变弱。

在主成像相机成像过程中，高速小面阵相机获取与主相机同光轴的图像，并与上一采样周期所得图像进行相关运算，可获得高速面阵相机两次曝光时间内像移量，空间相机为刚性连接，高速面阵相机和主成像TDICCD具有相同的扰动量，通过测量探测相机图像序列间的像移量，由主成像TDICCD与探测相机的位置关系和像元尺寸等相机参数即可求出主成像相机成像过程中的像移量，当前的图像数据储存起来将作为下一次测量的基准。通过不断检测高速图像的像移信息，即可测出主成像相机成像过程中的扰动量，用于实时校正或后期复原。

3 像移测量算法

图像相关算法是像移探测的关键，其性能优劣直接影响到探测系统的精度，进而影响图像质量，而其计算效率也决定了探测数据是否可用于实时补偿。为克服高速探测CCD图像序列的高噪声问题，本文采用相位相关算法来测量像移数据。相位相关法是一种非线性、基于图像傅里叶变换的频域相关算法，该算法取图像频域中的相位信息，减少了对图像内容的依赖性，具有优良的抗噪性能。同时本文利用局部采样来克服全局采样的高运算量、高存储量的缺点，实现高效精确的亚像素测量。

3.1相位相关法

相位相关法的理论依据是傅里叶变换的平移性质，图片在空间域中的平移，在频域中表现为线性相位差。假设两幅图像f1(x,y)和f2(x,y)之间，存在相对像移量，且平移量为(Δx,Δy)，则有

(1)

对式(1)两边分别进行傅里叶变换，由傅里叶变换的平移性质可以得出

(2)

式(2)中F1和F2分别为图像f1和f2的傅里叶变换。提取式(2)的相位，即两幅图像归一化互功率谱G(u,v)为

(3)

式中：F2*(u,v)为F2(u,v)的复共轭。

通常，求解(Δx,Δy)有以下两种方法[8]：

(1)将两幅图片频域中的相位差向两个频率轴投影，可以直接计算得到(Δx,Δy)，但这种方法对噪声非常敏感；

(2)根据傅里叶变换的平移性质，图片空间域的平移可转化为图像频域中的相位差，通过求归一化互功率谱的反傅里叶变换得到2维冲激函数δ(x-Δx,y-Δy)，检测其峰值所处的位置即可得到两幅图片的像移量(Δx,Δy)，如图2所示。

图2 相位相关法示意图

对于无限域的连续图像来说，式(3)是成立的。然而在实际运算中，图像都是有界且离散的，这使得单位冲激函数转化为离散时间单位冲激序列的形式。而且，两幅具有像移的图片包含不重叠的内容，使得两幅图像互功率谱相位的反变换，总是含有一个相关峰和一些非相关峰，相关峰的能量对应重叠区域的所占百分比。仿真实验显示，当两幅图像重合区域很小时，相位相关法仍能提供较满意的结果。图3可以看出两幅只有50%的重合区域时，峰值依然尖锐突出。可见相位相关法可以很好地适应TDICCD成像中高速图像序列具有较大推扫像移的情况。但是仅对两幅图片进行相位相关运算，只能得到像素级的像移量，无法满足实际应用。

图3 重合度为50%图片的互相关功率谱

3.2局部上采样实现亚像素像移测量

信号上采样可采用频域补零填充的方式，提高傅里叶变换输出的分辨率，频域信号的零填充对应时域信号的理想插值[9]。对相位相关的功率谱内插零填充，傅里叶反变换即可得到上采样后的互相关峰值，检测细化后峰值位置，就可以得出亚像素级的像移量。而对整个功率谱进行补零上采样，将会导致存储需求急剧增加，运算效率下降。如图4所示256×256像素的图像序列，理论上要达到0.1的像素精度，则要计算和存储2560×2560的功率谱数据，使得正反傅里叶变换的计算量大幅增加。随着

像移测量精度的增加，全局上采样将不利于实际应用。为减少存储量提高运算效率，利用矩阵乘法只对相关峰值附近一个较小的邻域进行上采样，忽略与所关心区域无关的信息，减少了对存储空间的需求，提高运算效率，而且能得到与全局上采样等效的结果。

对于图片互功率谱的响应函数δ(x-Δx,y-Δy)，在(Δx,Δy)周围定义一个尺度为m的邻域L=[Xm,Ym]，Xm=(Δx-m/2,Δx+m/2)，Ym=(Δy-m/2,Δy+m/2)，对该领域进行k倍上采样，则采样步长为1/k，由傅里叶反变换的矩阵乘积表达式[8]可得

(4)

式中：G(U,V)为互功率谱的矩阵表示，X′=[Δx-m/2,Δx-m/2+1/k,Δx-m/2+2/k,…,Δx+m/2]，Y′=[Δy-m/2,Δy-m/2+1/k,Δy-m/2+2/k,…,Δy+m/2]，g(X′,Y′)为局部上采样后的响应函数，维度为mk×mk。

局部上采样取整个频域空间的信息实现小区域的采样放大，是一种高效准确的亚像素定位方法，上采样尺度因子为k时，理论定位精度可达1/k像素，如图5所示，256×256像素的图像序列，理论上要定到0.1的像素精度，利用局部上采样则只需计算和存储15×15的数据。

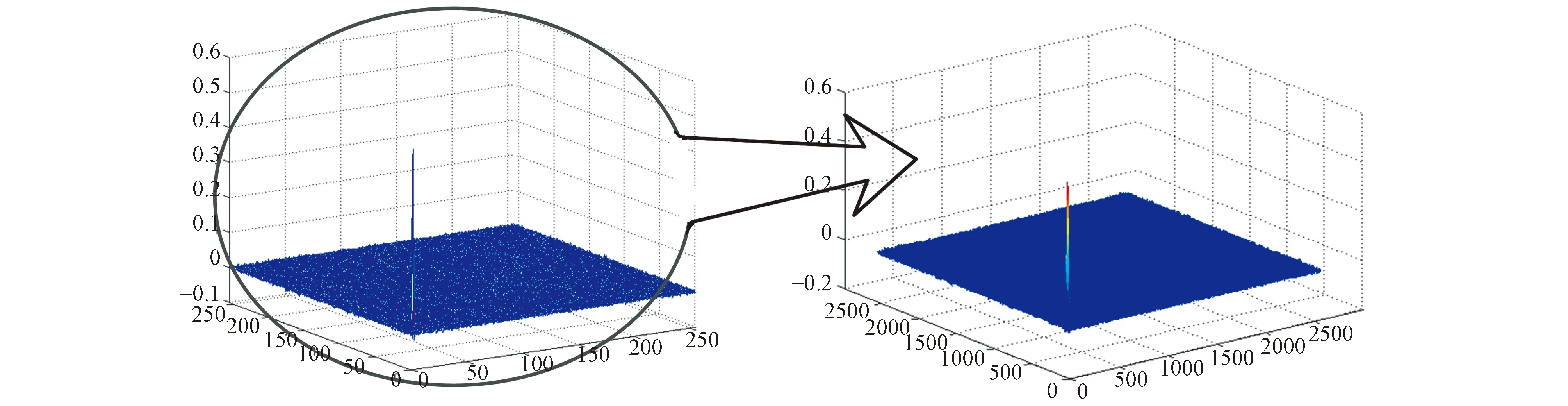
图4 全局上采样示意图

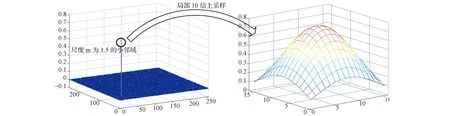
图5 局部上采样示意图

4 仿真分析

基于局部上采样的相位相关法测量图像像移的流程如图6所示，算法的主要步骤如下：(1)仿真生成具有亚像素像移的高速图像序列；(2)利用传统的相位相关法得到整像素的平移量(x，y)；(3)对整像素定位点(x，y)周围1.5×1.5领域范围内进行k倍上采样，得到细化的相关峰值，得到与中心位置的偏移值(Δx，Δy)，最终得到亚像素级的平移量(x_sub，y_sub)。由于传统的相位相关法具有像素级的精度，上采样区域为整像素定位点1.5×1.5范围，可保证亚像素定位点在此范围内。本文中上采样倍率k取100，则理论上亚像素测量精度能达到0.01个像元。

图6 亚像素像移测量算法流程图

为验证本文提出的像移测量方法的性能，对其进行了大量对比试验和适应性实验，仿真实验用的模板图像为某遥感卫星拍摄的灰度图片如图7所示，具有亚像素像移的高速图片(256×256)序列由Matlab中的图像处理工具箱(IPT)的仿射变换函数截取生成。

图7 某遥感卫星拍摄图片

1)TDICCD相机像移的定量分析

对于轨道高度为500 km，星下点像元分辨率为0.5 m的高分辨率相机，假设TDICCD的级数为128，像元尺寸为10 μm，单级积分时间为0.07 ms，则相机推扫通过星下点0.5 m的时间为0.07 ms，TDICCD成一行像的积分时间为8.96 ms。高速探测器选定为成像帧频为2000 帧/s、分辨率为256×256的高速CCD，且其像元尺寸与TDICCD的像元尺寸相同，则一个积分周期高速CCD将拍摄17.92幅图片，前后两帧图像将有7.1个像元的推扫像移。由于卫星的空间运行环境复杂，非正常像移具有很大的随机性，基本上没有规律可循。从实际应用的成本方面考虑，本实验综合考虑各种因素对像移的影响，利用总的像移数据进行实验仿真。在无补偿的极限情况下，一个积分周期内，TDICCD在线阵方向上像移将达到约14个像元，推扫方向的像移也达到6个像元，则高速CCD图像序列间的随机像移幅值在线阵方向和推扫方向分别为0.77个像元和0.33个像元[1,3,7,10]。

2)针对TDICCD相机成像模式的仿真实验

考虑到TDICCD相机成像过程中，高速图片序列像移特性，利用IPT工具箱的仿射变换生成3组有随机像移的图像序列，每个图像序列有18帧图片，图像的行方向即推扫方向的像移由7.1个像元的推扫像移和像移范围在±0.8像元内的随机像移组成，图像的列方向即线阵方向像移为±0.4像元内的随机像移。仿真数据示意见图8，像移测量结果见表1。

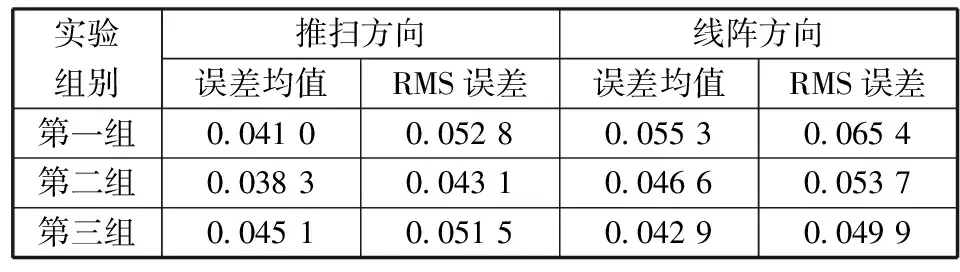
表1 本文方法像移测量结果

从表1中数据可以看出本文中算法性能优越，在亚像素定位上多次测量的均方根(RMS)误差均优于0.1个像元，可以适应TDICCD的成像模式。

3)随机噪声实验

为测试文中方法对图片随机噪声的适应性，在一组图像序列(18帧图片)添加不同信噪比(SNR)，均值为0的高斯白噪声(图9)，信噪比∞表示图片不添加任何随机噪声，图像序列具有相同的随机像移，且像移范围在±1个像元内。图10通过直方图直观地列出本文方法在多种噪声下的像移测量RMS误差。

图9 添加不同信噪比的高斯白噪声后的图像

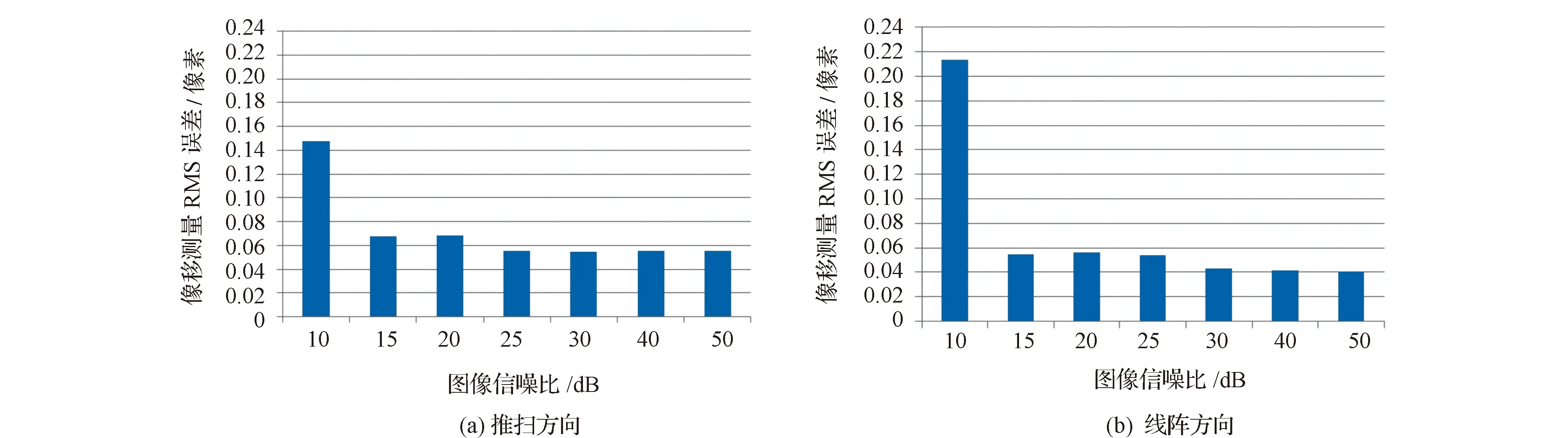
图10 图像信噪比对亚像素像移测量误差的影响

从图10可以看出本文方法对图片随机噪声有较好的适应能力，在图像信噪比为15 dB时，均方根误差仍优于0.1个像元。

4)灰度变化适应性实验

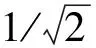
图11 图片灰度变化类型

表2 不同灰度变化下的像移测量结果

从表2数据可以看出，对于不同灰度变化像移测量的最大误差在推扫方向和线阵方向都为0.05个像元。实验证明，本文方法对图像灰度值变化也有很好的适应能力。

5 结束语

高精度像移信息的获取是获取高分辨率图像的基础和前提，是当前的研究热点。本文主要对像移测量方法进行了研究，针对高分辨率TDICCD相机，提出高速图像采集与相位相关法结合像移直接测量的方法，仿真实验表明该方法在测量精度和抗噪性方面性能优越，可应用于实际的像移探测系统。下一步的工作是搭建相机实验平台，着力于该方法硬件实现，特别是相位相关法的快速运算。

References)

[1]李晓云, 杜伟. 星载TDICCD 相机像移对成像质量的影响分析[J]. 航天器工程, 2011, 20(3):51-55

Li Xiaoyun, Du Wei. Analysis of image motion effect on satellite tdiccd camera image quality[J]. Spacecraft Engineering, 2011, 20(3):51-55 (in Chinese)

[2]陈荣利，李英才，樊学武. TDICCD相机像质综合评价研究[J].航天返回与遥感，2003, 24(4):10-13

Chen Rongli, Li Yingcai, Fan Xuewu. Investigation on synthetically evaluating image quality of TDI-CCD cameras[J]. Spacecraft Recovery & Remote Sensing, 2003, 24(4):10-13 (in Chinese)

[3]Sylvie R, Loic J, Bernard Rouge, et al. Satellite attitude instability effects on stereo images[J].IEEE International Conference on Acoustics Speech and Signal Processing, 2004,9(4):477-480

[4]徐鹏,黄长宁,王涌天. 卫星振动对成像质量影响的仿真分析[J]. 宇航学报, 2003, 24(3):256-263

Xu Peng, Huang Changning, Wang Yongtian. Modulation transfer function in push-broom camera limits resulting from mechanical vibration[J]. Journal of Astronautics, 2003, 24(3):256-263 (in Chinese)

[5]周虎. 航天光学遥感器抖动补偿方法研究[D]. 北京：中国空间技术研究院，2008

Zhou hu.Studies on jitter compensation methods of space optical remote sensor[D]. Beijing：China Academy of Space Technology，2008 (in Chinese)

[6]葛任伟,吴清文,王运. 基于联合变换相关器的像移测量方法研究[J]. 计算机仿真，2010, 27(3):215-219

Ge Renwei, Wu Qingwen,Wang Yun. The study of image motion measurement based on joint transform correlator[J]. Computer Simulation, 2010, 27(3):215-219 (in Chinese)

[7]樊超，李英才，易红伟. 颤振对TDICCD相机像质的影响分析[J]. 光子学报，2007，36(9)：1714-1717.

Fan Chao, Li Yingcai, Yi Hongwei. Influence analysis of buffeting on image quality of TDICCD camera[J]. Acta Photonica Sinica, 2007, 36(9):1714-1717 (in Chinese)

[8]王彩玲，程勇，赵春霞. 局部相位相关用于图像亚像素级配准技术研究[J]. 中国图象图形学报, 2011, 16(3): 427-432

Wang Cailing, Cheng Yong, Zhao Chunxia. Robust subpixel image registration technique based on local phase correlation[J]. Journal of Image and Graphics, 2011, 16(3): 427-432 (in Chinese)

[9]Smith J O. Mathematics of the discrete fourier transform[M]. Stanford: CCRMA, 2002: 145-179

[10]景泉. 敏捷卫星偏流角计算模型研究[J] . 航天器工程, 2012, 21(4):16-20

Jing Quan. Research on computation model of bias angle for agile satellite[J]. Spacecraft Engineering, 2011, 20(3):51-55 (in Chinese)

[11]陈跃庭,徐之海,李奇. 低曝光量下投影算法的稳健性研究[J]. 光学学报, 2007, 27(2):238-242

Chen Yueting, Xu Zhihai,Li Qi. Robustness of projection algorithm for uder-exposured images[J]. Acta Optica Sinica, 2007, 27(2):238-242 (in Chinese)

(编辑：张小琳)

TDICCD Space Camera Image Motion Measurement Based on Phase Correlation

HU Chao WANG Xiaoyong GUO Chongling

(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)

Obtaining image motion information during space camera imaging for real-time compensation for hardware or post-time restoration is an important means to improve resolving power of high-resolution space camera. Achieving high measurement precision of sub-pixel is always a technical problem. According to the imaging characters of high-resolution TDICCD camera, this paper proposes a method to directly measure image motion. The method uses high-speed image sensor to acquire image sequence, and then adopts phase correlation algorithm based on the local frequency sampling to determine the sub-pixel image motion curve. Matlab simulation experiments show that the method has high tolerance of image noise and grayscale change，and its measurement accuracy is better than 0.1pixel when the SNR of images is higher than 10dB.

phase correlation; TDICCD camera; high-resolution; image motion measurement; sub-pixel

2014-02-11；

：2014-05-06

胡超，男，硕士研究生，研究方向为航天光学遥感器总体设计。Email：chaohero@qq.com。

V19；TP751.1

：ADOI：10.3969/j.issn.1673-8748.2014.03.006