数学教师纠错教学策略研究*——从处理学生解题错误谈起

陈建华 文 清

(1.扬州大学 江苏扬州 225002； 2.成都大学 四川成都 610106)

数学教师纠错教学策略研究*
——从处理学生解题错误谈起

陈建华1文 清2

(1.扬州大学 江苏扬州 225002； 2.成都大学 四川成都 610106)

教师的学科知识不能自动地产生成功的教学方式和教学理念；缺乏坚固的学科支撑，成功的教学方式和新颖的教学理念不可能实现。为了支持学生更深入学习高等数学，教师应该不断积累、完善自己的数学教学知识结构，聚焦课堂教学实践与反思，走向开拓性教学。通过教师对学生产生解题错误的不同教学处理，考察教师纠错教学策略。借助习题涉及教学内容的知识包，探讨数学教师掌握教学内容知识的深度、广度对教学的影响，以及数学教师纠错教学策略。

数学教师；纠错教学策略；矩阵；零因子；秩；线性方程组；知识包

线性代数内容抽象，知识点间联系紧密。它在给学生提供数学思维训练素材的同时，也给学生理解课程的概念和法则甚至计算都带来困难，亦给教师的教学带来难度。基于课堂教学实践的访谈，也是评价教师知识常见的方法之一[1]。本文通过教师对学生解题错误的不同教学处理，了解任课教师对线性代数纠错教学能力的现状。借助相关教学内容的知识包，讨论数学教师掌握教学内容知识的深广度对教学的影响，以及数学教师学科水平与教学能力契合的发展方向。

一、一道线性代数试题引出的话题

(一)从学期考试中获得的问题情境

这是一道貌似简单实质蕴含深刻的智慧的检测学生矩阵的概念、计算等及相关知识联系教学的有价值的题目，既考查学生基础知识又考查其分析、解决问题的能力，还考查其严谨治学的意识。

2013年1月，将上题作为一道解答题植入线性代数课程期末试卷，为了保证测试调查的真实性、有效性，将其编排在试卷的前半部分。阅卷后，随机选取两个班级，进行了答题情况统计。结果如下：学生人数72人(不考虑重修学生)，未做解答的5人，获得结论“k=-3”的65人中，理由正确的有36人，理由不正确的有29人。不正确的推理过程主要有两类：

错解(1)：因为AB=O，且B≠O，所以A=O，故行列式|A|=0。

错解(2)：因为AB=O，所以|A|·|B|=0，由于B≠O,故|B|≠0，从而行列式|A|=0。

(二)从问题情境中引出的话题

请您花点时间考虑一下：如果您的学生发生上述错误，您认为：学生产生错误的原因是什么？教学中怎样帮助学生改正错误？

(三)讨论话题的对象

本年度讲授过线性代数课程的大学数学教师，共18人。为了叙述方便用教师姓名拼音首字母代替某教师，其中新教师(教龄4年以下，用N表示)6人，经验型教师(教龄4年以上)12人。本科学历1人，硕士学历4人，博士学历(用D表示)13人；具有代数知识背景(攻读硕士、博士阶段是基础数学代数方向，用A表示)的6人；具有教学知识背景(即本科阶段是师范专业，用T表示)的12人。

二、学生解题错误成因与教学策略的讨论

本研究中的所有教师都认为，学生在进行矩阵乘法的运算中用错了运算律， 行列式和矩阵概念理解出现了问题。然而，他们在解释学生解题出错原因和如何帮助学生改正该错误时表达了不同的见解。

(一)学生解题错误成因讨论

新教师在讨论学生的错误时，6位教师都认为错解(1)是由于学生对矩阵的乘法理解不深刻。错解(2)是将零矩阵和矩阵的行列式为零两个概念混淆了。在解释学生的错误的过程时，虽然，ZJW(DN)是新教师，但她的分析还是简洁明了的：

矩阵的乘法运算中存在零因子，即两非零矩阵的乘积可能为零矩阵，部分学生形成错解(1)，是由于对此疏忽造成的。我们可以通过一些例子来提醒学生注意，比如可以给学生下列例子：

另外5位新教师，也像ZJW这样，虽然提及“零因子”或“方阵的行列式”，但他们没有给学生提供反例，或告诉学生阅读教材的相应部分，让学生关注基本概念或运算律。关于解题的思维过程，一位新教师认为从解题的角度看，要求k值，当然只有|A|=0，才能推出具体数值。他认为学生不必过多纠缠“为什么”，倾向于让学生记忆其思维模块。由此可以看出，这些教师未想到要促进学生对矩阵乘法运算的深入理解，明晰混淆的概念；仅仅是从解题需要出发，建议学生如何做题。虽然他们的教学法理解有概念性理解的倾向，但还是处于过程性理解阶段[2]。

虽然经验型教师解释学生的错误总体而言与新教师有相同之处，但他们更期望学生能够学会更多而不仅仅是例子，希望学生学会在这个运算法则下所蕴含的数学原理。概念组的教师关注矩阵运算系统和实数运算系统，指出矩阵与行列式的本质区别，能提醒学生从函数的角度，理解方阵行列式的联系。如JRZ(DAT)给出解释是：

矩阵代数系统Mn(R)与我们熟悉的实数系统R的本质区别是在Mn(R)中存在零因子，消去律不成立，而实数系统中不存在零因子。我会给学生一个对照表，将矩阵系统和实数系统作一个比较，让学生区分两个系统，以加深对问题的理解。

实数集合R矩阵集合Mn(R)结合律、分配律结合律、分配律交换律、消去律零因子元素a可逆⇔存在b使得ab=ba=1⇔a≠0⇔存在b使得ab=1元素A可逆⇔存在B使得AB=BA=EA⇔|A|≠0⇔存在B使得AB=E

关于a≠0与|A|≠0从代数角度抽象地看，二者无任何差别。虽然矩阵的记号(数表外加括号)与行列式记号(数表外加两竖线)很相像，但它们是两个截然不同的概念，行列式是一个数，而矩阵为一个矩形的数列表。一方面，只有方阵才可能取行列式；另一方面，方阵与它的行列式又是密切相关的，行列式是方阵特性的重要标志，提高一个层面看，可以把矩阵(对应于一个数)看成方阵的函数。

事实上，对任意的A∈Mn(R)，如何定义其函数值f(A)，在不同的领域有多种不同的回答，矩阵A对应于|A|只是其中一种意义深刻的对应方法，比如行列式是否为零，把矩阵划分为奇异和非奇异两类。当我们将方阵的行列式概念推广为矩阵的行列式的概念后，可以揭示出矩阵更深刻的特性，人们通常认为方阵的行列式概念是讲授矩阵秩的先导。所有这些充分传达了教师们对课题的概念性理解，对方阵行列式的核心思想的把握。

一部分有教学法知识背景的教师对学生的错误的解释表现出特定的视角。他们认为：从学生的学习过程看，学生发生这两类错误的根本原因是“存在矩阵B≠O”抽象造成的。如果题目中矩阵是具体给出的，学生的求解不就是剩下矩阵的乘法运算了吗?应该从“存在矩阵B≠O”的作用是什么开始考虑问题：一个元素不为零、一列向量不为零或整个矩阵不为零，它们又能联系哪些相关知识点或结论呢？面对有44.62%的学生就此题出现错误的现象，说明这是帮助学生正确运用矩阵运算律、辨别矩阵与行列式概念的极好素材。教学中要好好利用这一宝贵教学资源，达到“留得残荷听雨声的”教学效果。

(二)纠错教学策略讨论

两组教师对学生的错误的解释不同，同样处理学生错误的策略也有不同的方法。两位新教师认为，之所以出错是学生没有很好地利用矩阵分块的技巧，如果学生能够想到将矩阵分块B=(β1，β2，β3)，则有AB=(Aβ1,Aβ2,Aβ3)=O，自然会联系齐次线性方程组AX=0。这两位教师用语言说明了推理过程和步骤。

与新教师的“大框架”给学生提供问题思路的指导不同的是，经验型教师的指导显得更细致，他们希望学生清楚每一步推导的理由。如SHC(T)是一位从事大学数学教学二十多年的老教师，他认为必须给学生详细的解题过程指导：

记B=(β1,β2，β3)，则AB=O⟺A(β1,β2，β3)=O(将矩阵B作列分块)⟺(Aβ1,Aβ2,Aβ3)=O(分块矩阵的乘法运算)⟺Aβ1=O(i=1,2,3)(分块矩阵的相等)⟺β1(i=1,2,3)是齐次齐次线性方程组AX=O的解。⟹AX=O有非零解(因为B≠O，所以存在βi≠0)⟹|A|=0。

对于如何恰当地利用分块矩阵进行矩阵的乘法，使之便于运算或论证，这是一个复杂且技巧性很高的问题。虽然矩阵的列分块方法是常见的分块方法，但结合本文讨论的问题，到底是如何联系上的呢？笔者进行如下追问：“您为什么会想到对矩阵B做列分块？”SHC(T)：“为什么？可能是长期教授该课程，好像见到AB=O，总能想到将矩阵B分块，然后联系上齐次线性方程组AX=0。”笔者：“如果对矩阵A做列分块，能获得解题思路吗？”SHC(T)：“应该可以的吧，还没考虑过。”

矩阵分块法是矩阵计算中的一种技巧，其好处在于矩阵分块后，能够突出该矩阵的结构，从而可以利用它的特殊结构，使得运算简化；除了将运算调理化外，还可以为某些命题的证明提供方法和思路。如将m×n矩阵进行分块A=(α1,α2,…，αm)，那么，在运算中，它可以视为一个“向量”，这时矩阵等同于它的列向量组。由此，理解矩阵与向量组的关系，这是对矩阵概念的深化，也是后续内容中利用矩阵来讨论向量组的基础。

带着某些特定的期望，笔者访谈了一位有代数背景的老教师SJH(DAT)。在介绍基本情况后，直接询问他：“您是如何联系齐次线性方程组的？您会怎样给学生提供思考问题的策略？”他说：

题目条件“AB=O,B≠O”的本质是思考问题的关键，于是我们可以从B≠O仔细考虑。若B≠O理解为有一个元素不为零，则在AB=O中矩阵A与一个元素相乘不好解释，所以接着从该非零元素所在的列不为零考虑，则有Aβ=O，且β≠O，这样克莱姆法则的结论自然联系上。

SJH(DAT)稍稍思考后接着说：

若B≠O，从矩阵的秩不为零(即R(B)≥1)考虑，由AB=O，知道R(A)+R(B)≤3，从而R(A)≤2，则有|A|=0。问题也得到解决。

教师期望学生所知道的与教师自己的知识是相关的，仅仅期望学生学会这个过程的教师，往往只有过程性的理解。同时，有限的学科知识限制了教师促进学生概念学习能力的培养。一位长期从事硕士研究生入学辅导的教师WJC(DAT)，他给出的纠错教学策略是：

此题思考的焦点是方阵的行列式，我认为中间结论|A|=0，应该可以猜测得到。而(非)奇异矩阵是线性代数中最重要和最基本的概念之一，沿着此思路，可以让学生回忆刻划|A|=0的等价条件，寻找解题思路。

根据WJC(DAT)的访谈整理得如下对照表：

|A|=0的等价条件解题思路AX=O有非零解将矩阵B作列分块,由AB=O,B≠O判断AX=O有非零解,故|A|=0A的秩小于3利用关系R(A)+R(B)≤3,且B≠O,从而R(A)≤2,故|A|=0A的列向量组线性相关将A做列分块,A=(α1,α2,α3),由AB=O,B≠O,不妨令β=(k1,k2,k3)T≠0,则有k1α1+k2α2+k3α3=0,故A的列向量组线性相关,从而|A|=0A有特征值为零(|A|=λ1λ2λ3)由于B≠O,不妨令β为B的非零列向量,则由AB=O有Aβ=O=O·β,从而,矩阵有一个特征值为零,β是A的属于0的特征向量,故|A|=0

教学实践中，注重教学方法、关注学生学习过程的有3位教师，其中1人是教育学硕士，1人是课程与教学论方向博士。他们在学生出现错误的成因分析和纠错教学策略指导中都能充分考虑学生学习习惯，有2位教师是采用反证法推导矩阵行列式|A|=0。QLL(T)教师认为：

从方法论的角度看，当我们正面思考问题受阻时，可以尝试从反面考虑，假设矩阵A的行列式不为零，即|A|≠0，则它是可逆矩阵，在等式AB=O两边左乘A-1，则有A-1AB=A-1O，由此推出B=O与题设矛盾。

该思路简洁明了，充分体现了“正难则反”的思维模式的威力。利用A-1这一具体对象交给将刚踏入全新矩阵运算系统的学生，避免了“无从着手，空中楼阁”的困惑。这里方法论知识对问题的解决发挥了决定性的作用。

课程与教学论方向博士ZBD(DT)的指导策略是为犯错误学生提供诊断性练习。她设计了帮助学生“诊断错误、解决问题”的一串练习题，试图通过这些练习提出过程背后的概念性问题。

习题1 设非零矩阵

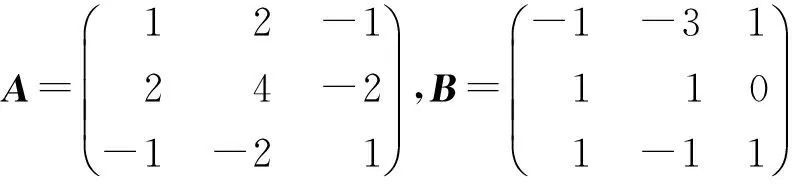
计算AB。由计算结果与题设条件比较，你发现了矩阵运算的什么特性？

计算矩阵的行列式|A|，思考零矩阵与矩阵行列式为零的区别与联系。

分别求非零矩阵

使得AB=O，其中R(B1)=R(B2)=R(B3)=1。

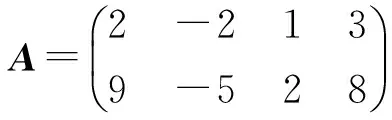
尽管这串习题从计算的角度看是从过程性方面开始的，但计算后的思考又让学生回到概念，通过该习题串成功地帮助学生在理解的基础上记住矩阵运算的若干规则。从教学角度看，既为学生指明思考问题的方向，又让学生自己去发现错误、纠正错误。此外，教师们还提到一些基于学习的策略，如组织学生学习、帮助学生观察、指导学生参与讨论等。

三、学科知识与教学策略关系的讨论

(一)知识包的建立和分析

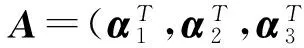
综合分析讨论的过程，我们可以获得关于本文所研究习题的一个知识包(图1)。知识包中椭圆表示研究课题，圆角长方形表示相关知识点，通过有向线段联系相关知识点；所有部分都明显地与研究习题有关，知识包的下层支持对学生错误的解释，上层则对教师给学生提供解题策略提供有力支持。

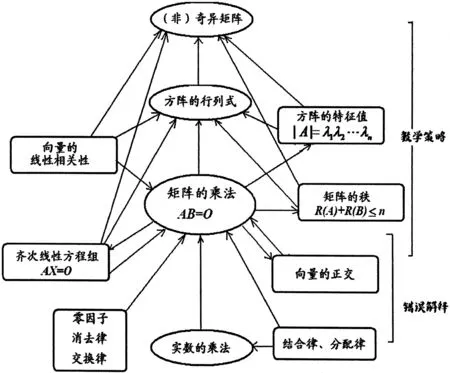
图1 习题的知识包

知识包中的概念是浓缩的知识点，也是教学中师生思维的“细胞”。教学中可以从关键知识点，揭示其被掩盖的特殊情况，如“矩阵B≠O”背后的“∃bij≠O”或“∃βj≠O”或“R(B)≥1”等，通过给出各种具体模式，帮助学生理解。也可以区分概念的异同，寻找它们的关键之处。

从学科知识的角度来看，参加讨论的教师的知识理解几乎都包含在这个包内。关于问题解决的教学策略，“奇异矩阵”几乎是所有教师都能意识到的关键概念。大多数新教师考虑问题限制在解释错误和解答问题范围内。而经验型教师，特别是有代数专业方向背景，或具有教学需求的教师(如SJH(DAT)和WJC(DAT))，能够很“轻松”地从较多角度讨论相关内容。这说明：专业知识背景的不同、教学知识的差异影响对知识包的相关各成分的了解范围，导致教师教学策略的优劣。

(二)“概念性理解”并非简单

新教师理解的深刻程度较浅，只能将知识包中少数元素引入问题的解决过程，且较为孤立。6位新教师中，关于错误解释有2人在过程性理解层面，4人在概念性理解层面；从教学策略角度看，只有1位教师达到概念性取向。经验型教师中，也只有具有代数背景的，或有教学需要的教师才有发展完全的、组织良好的概念性理解的知识包。统计表明：在12名经验教师中，有10名(占83%)关于错误解释在概念性理解层面；从教学策略角度看，只有8位教师达到概念性取向。图2显示了教师关于该内容的学科知识，图3显示了教师在认识和处理该问题时的教学法倾向。

图2

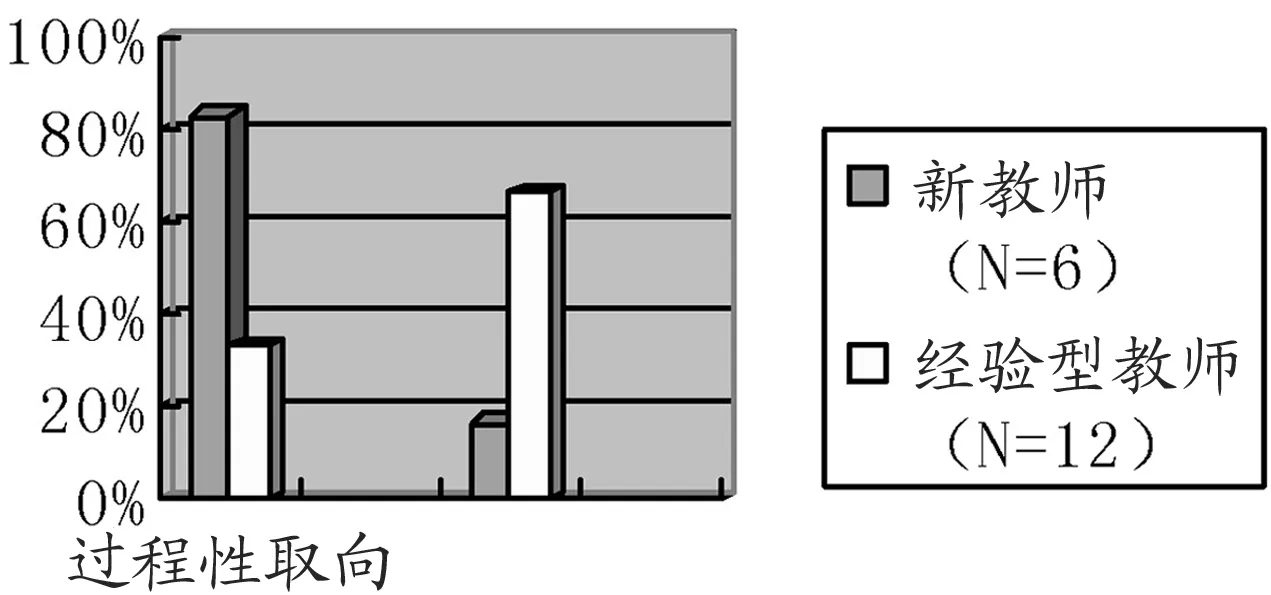
图3

无论是新教师还是经验型教师，从教学策略上看概念性取向的人数要比解释错误时概念性理解的人数要少。这提示我们，数学知识的“概念性理解”并非简单。访谈调查中，ZBD老师设计的习题串，从问题形式挖掘学生的思维过程，从学生的立场解释知识、表征知识，能促进学生对数学知识的理解从过程性转向概念性，给我们很好的启示。

(三)若干思考

大学数学教师怎样准确认识学生的错误，游刃有余地矫治错误，达到对讲授学科知识的深刻理解?本课题的研究给我们一些启示：

第一，教师的学科知识具有促进学生在课题学习中获得特殊智慧的特征。数学教师往往会在相关课题之间和课题内部的知识之间建立一些联系，形成中心概念、概念序列或概念节点，而如何创设知识点之间的联结并形成一定的“知识包”，则需要教师自觉总结或在教研活动中共同讨论。

第二，多角度地考虑问题，讨论各种解法，是数学发展的一种持续的动力，也是数学教学追求的目标。计算过程、推理路径的多样化，源于概念性理解。一个问题能用多种方法计算或论证需要超越知识表面的形式，把握数学的精髓——蕴含的数学概念和原理。

第三，教育教学活动是复杂的、多变的，仅仅具备学科基础性知识，并不足以保证数学教师能够胜任数学教育实践工作[3]。虽然大部分教师能够顾及学生的认知水平，但具体操作中，有良好的教学法知识的教师，能更有效地帮助学生认识错误、矫治错误，表现出了更有章法的指导策略。

总而言之，教师的学科知识不能自动地产生成功的教学方式和教学理念；缺乏坚固的学科支撑，成功的教学方式和新颖的教学理念不可能实现[4]。我们期望做一个“WJC+QLL+ZBD”型即学科专业扎实、教育教学智慧、实践反思深刻、睿智耐心的数学教师，为了支持学生更深入学习高等数学，我们应该不断积累、完善自己的数学教学知识结构，聚焦课堂教学实践与反思，走向开拓性教学。

[1]黄兴丰，马云鹏.美国数学教师学科知识评价方法的述评[J].数学教育学报，2013，(1).

[2]马 复.试论数学理解的两种类型——从斯根普的工作谈起[J].数学教育学报，2001，(3).

[4]马立平.小学数学的掌握与教学[M].李士钅奇等译.上海：华东师范大学出版社，2011.

[5]陈建华，刘金林，魏俊潮.线性代数(第3版)[M].北京：机械工业出版社，2011.

[6]陈建华，李立斌，凌 智，刘金林，陈惠香.基于问题解决的线性代数课程教学设计研究[J].高等理科教育，2011，(4).

(责任编辑：李文富)

Study on Mathematics Teachers' Teaching Strategies of Error Correction——Based on Error Handling in Students' Problem Solving

Chen Jian-hua1Wen Qing2

(1.Yangzhou University, Yangzhou, Jiangsu, 225002, China; 2.Chengdu University, Chengdu, Sichuan, 610106, China)

Teacher's discipline knowledge can't automatically produce successful teaching modes and teaching ideas.Without strong subject support,the success of teaching methods and new teaching ideas is impossible.In order to help students study more deeply,university mathematics teachers should accumulate and improve their mathematics teaching knowledge structure,focus on classroom teaching practice,and achieve the pioneering teaching.Through teachers' different teaching to students' incorrect answers, we can observe teachers' teaching ability of error correction.By means of the knowledge package involved with teaching content, this article discusses the depth and width of teachers' teaching content knowledge,their influence on teaching, and mathematics teachers' error correction strategies.

mathematics teachers;teaching strategies of error correction;matrices;zero factor;rank;systems of linear equations;knowledge

2014-03-09

扬州大学教改课题“基于数学理解的线性代数课程教学实践研究”(YZUJX2012-46B)。

陈建华(1963—)，男，扬州大学副教授，硕士生导师。研究方向：线性代数。

G645

A

1674-6120(2014)06-0049-05