基于小波神经网络的液压泵故障类型识别
2014-07-18董秋武汪宝生
董秋武,汪宝生
(广东伊之密精密机械股份有限公司,广东佛山528306)
液压泵作为液压系统的动力元件,是液压系统的核心元件,其性能的好坏直接关系到整个系统的的稳定性和可靠性。同时液压泵也是整个液压系统中最易损坏的元件,由于液压泵特别是国外的液压泵,其价格比较昂贵,所以对于损坏的液压泵一般都要经过维修后重新使用。然而液压泵故障部位具有隐蔽。液压泵在长时间的运转过程中,液压泵内部各配件之间因发生相互摩擦,各配件就会产生磨损。对于液压泵的磨损有些是属于正常磨损,对液压泵的性能不会产生影响,但有些磨损却会影响到液压泵的正常使用,使其内泄较大,压力和流量都达不到要求。对于液压泵的磨损故障仅仅靠维修人员通过目测诊断故障部位很容易造成诊断错误,因此智能化故障诊断对液压泵维修来说是十分必要的。
在液压泵故障诊断方面,国内外已有很多相关的研究。目前,对液压泵故障诊断的方法大部分借鉴于用于机械故障诊断的方法。常用的诊断方法有专家系统诊断方法、AR模型法[1]、状态估计法[2]、参数模型法[3]、神经网络法。近几年来随着信号处理技术的发展,一些新的研究方法在故障诊断方面得到了广泛的运用,如小波变换、Hilbert变换方法、Huang变换方法等。
虽然目前对液压泵故障诊断方面的研究较多,但对于液压泵故障类型识别的方法却很少。这主要由于液压泵测试的过程中会受到各种干扰,很难排除这些干扰。再者,液压泵内部配件出现磨损产生的特征很难用精确的数学表达式或其他信息表示出来,这给故障类型识别带来了一定的难度。由于液压泵内部配件,如配油盘、活塞、缸体磨损程度的不同,表现出其特征频率不一定相同,但其在每个频率段所产生的能量比是不一样的。本文作者根据这一特征提出了小波神经网络对故障部位进行识别。
1 小波包分解
小波变换是傅里叶变换的新的发展,它既保留了傅里叶变换的优点,又弥补了傅里叶变换在信号分析上的一些不足,它在时-频域同时具有很好的局部化特性。由于正交基小波变换只对信号的低频部分做多层次的分解,而对高频部分 (即信号的细节部分)不再继续分解,因此小波变换能够很好地分析以低频信息为主要成分的信号,但它却不能很好地分析包含大量细节信息的信号,小波包变换可以对高频部分提供更精细的分解,这种分解既无疏漏,也无冗余,所以对包含大量中、高频信息的信号能够进行很好的时频局部化分析。
对于小波包的计算公式,首先选取一种小波母函数ψ(t)和对应的尺度函数φ(t),可以通过以下递推公式得到一组正交小波包函数[4]:

式中:ψ0(t)=ψ(t),ψ1(t)=φ(t),h(k)和g(k)分别是对应于ψ(t)和尺度函数φ(t)的正交镜像系数。
相应地各节点处的小波包函数为
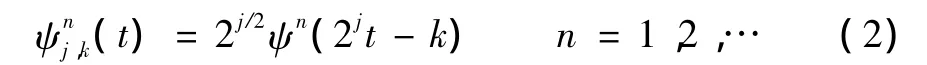
其中n,j,k分别为模数、尺度级数和时间平移参数。则对信号x(t)在各个节点上经过对应小波包函数分解后的系数为
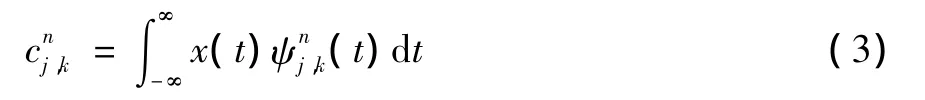
利用小波包提取信号特征并不能直接供系统模式识别。通过实验验证,使用节点系数的能量值作为信号特征供系统进行模式识别是十分有效的[5]。各节点系数的能量值可以通过以下公式得到:

式中:Enj表示信号在 (n,j)频率段所产生的能量。
为了防止在第n层分解各频率段的能量值相差过大,造成采用神经网络算法进行模式识别收敛速度过慢的现象。必须将第n层分解的各频率段能量变换到[0,1]区间上。可按以下公式进行变换:

2 BP神经网络算法
BP(Error Back Propagation Network)神经网络是目前应用最为广泛和成功的神经网络之一。其学习过程由信号的正向传播和误差的反向传播两个过程组成。输入样本从输入层输入,经隐层逐层处理后向输出层输出,若输出层的实际输出与期望输出不符合,则通过反馈误差修改各层的权值和阀值,以达到自学习的目的。
3 小波神经网络运用于液压泵故障类型识别
3.1 特征值的提取
采用液压泵后盖处振动为液压泵故障类型识别信号。液压泵通过联轴器和电机相连,由电机带动液压泵运转,电机的转速为1 500 r/min。采用精信JX30系列集成加速度传感器测量振动信号,将传感器垂直安装液压泵的后盖上。采用采样频率为1 024 Hz,采样点数为32 768个,采样时间为32 s进行采集,得到的4类信号如图1所示,分别为柱塞故障信号、配油盘故障信号、缸体故障信号和正常信号。为了能让计算机识别这4类信号,将这四类信号用0,1表示。[1 0 0 0]表示正常,[0 1 0 0]表示缸体故障,[0 0 1 0]表示配油盘故障,[0 0 0 1]表示柱塞故障。

图1 4种类别振动信号
把每类信号分割成64组,每组为512个采集点,一共可以得到256组特征信号,将这256组新组成的信号进行三层小波分解,分别求出第三层中每个波段的能量值并将每个波段的能量值进行归一化处理,将处理后的归一化能量值作为特征量。
图2—5分别为这4类型号中其中一组的三层小波包分解能量分布图。

图2 正常振动信号分解

图3 柱塞故障信号分解

图4 缸体故障信号分解
其中 (a),(b),(c),(d),(e),(f),(g),(h)分别表示第三层节点 (3,0),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(3,7)频率段上的能量分布。图中的横坐标表示采样点,纵坐标表示特征量。图2为正常信号的三层小波包分解图,从图中可以看出能量主要集中在 (3,0)和 (3,1)波段上。图3为柱塞故障分解图,从图中可以看出能量主要集中在 (3,2)和 (3,6)频率段。图4为缸体故障,能量集中在 (3,2)和 (3,6)上,但表现出来的幅值较大。图5为配油盘故障分解,能量主要集中在(3,1)、(3,2)、(3,6)和 (3,7)上。

图5 配油盘故障信号分解
3.2 BP神经网络故障类型识别
通过以上分析可知,一共可以得到256组特征量,将这256组特征量中的246组作为训练样本,剩余的10组作为测试样本。小波包三层分解,提取第三层的8个频率段的能量值作为特征量,因此BP神经网络模型的输入层为8个节点,要识别的是4种类型的故障,故输出层应为4个节点,对于隐层节点数可按下列公式求得:

式中:n1表示隐层节点数,n表示输入层节点数,m表示输出层节点数,a为 [1,10]之间的常数。
分别对隐层取8~11节点数进行训练,得出训练误差如表1所示,从表中可以看出隐层选取10个节点,训练误差最小。

表1 训练误差结果
BP神经网络各层节点数确定之后还必须确定其训练函数,采用Levenberg-Marquardt算法最为网络的训练函数。Levenberg-Marquardt算法源于 Newton算法[6],其算法在MATLAB中用trainlm函数表示。如图6所示,可以看出网络经12次左右就可以到大目标误差的要求,此时的训练误差为0.055 9。

图6 训练误差结果
等待训练完毕之后,将测试样本输入到BP神经网络层输入层对训练完毕的BP神经网络模式测试。通过测试结果可知,10个样本的识别率达到了100%。
4 测试结果
图7为运用小波神经网络编写的诊断软件对A7V0160系列泵诊断的结果图,图中显示了振动曲线,并显示出诊断结果为柱塞故障,在图的最下一栏还显示了建议维修方法。对被测试液压泵拆卸发现液压泵的柱塞出现了严重的磨损,如图8所示。通过测试证明采用小波神经网络对液压泵故障类型的识别可以取得较好的效果。

图7 诊断结果

图8 磨损的柱塞
5 结论
对液压泵柱塞故障、缸体故障、配油盘故障和正常这4种故障类型进行识别,提出了采用小波神经网络识别故障。分析和测试结果表明了以下几点:
(1)利用液压泵后盖振动作为测信号,可以作为故障类型识别的特征信号;
(2)用小波包对信号分解,提取出每个频率段信号的能量值作为模式识别的特征量,能解决故障频率不能用数学模型精确表示的问题。
(3)实验结果表明,BP神经网络对液压泵故障类型识别具有良好的效果。
采用小波包分解,并提取各频率段能量还可以用来预测液压泵的寿命,提出的方法还可以运用于其他旋转机械故障诊断。
[1]YOSHIDA H,KUMAR S.ARX and AFMM Model Based on Line Real-time Data Base Diagnosis of Sudden Fault in AHU of VAV System[J].Energy Conversion and Management,1999,40(11):1191 -1206.
[2]MARTIN K F.A Review by Discussion of Condition Monitoring and Fault Diagnosis in Machine Tools [J].Int.J.Math.Tools Mfg,1994,34(4):527 -551.
[3]MANRING N D,JOHNSON R E.Modelingand Designing a Variable-displacement Openloop Pump[J].Trans.ASME,J.Dynamic Syst.Measmt and Control,1996,118(2):267 -271.
[4]敖银辉,汪宝生.钻头磨损检测与剩余寿命评估[J].机械工程学报,2011(1):177-181.
[5]FUKUNAGA K.Introduction to Statistical Pattern Recognition[M].San Diego,CA,USA:Academic Press,Inc.1992.
[6]阮晓刚.神经计算科学[M].北京:国防工业出版社,2006.
