滤波器在运动控制器中的应用

任建功，冯斌，牟恩旭，黄晓勇

(西安交通大学机械工程学院，陕西西安710049)

滤波器在运动控制器中有着广泛的应用，在常见的数控系统中，如德国西门子数控系统和日本发那科数控系统，控制回路中都使用了滤波器［1－2］。在设计运动控制器过程中，滤波器的使用是十分必要的，对提升运动控制器的性能有着十分重要的作用。特别是在控制参数调整已经无法进一步改善控制器性能的情况下，滤波器作为一种工具，其使用能够起到很好的提升效果。

运动控制器中的滤波器，按照其特点划分为低通滤波器和带阻滤波器，其它要求的滤波器均可由二者的组合实现［3］。滤波器的主要用途是滤除噪声、干扰以及不需要的频率分量信号，抑制谐振现象，平滑运动控制器伯德图曲线以及增加控制系统的带宽［4－5］。以下主要讨论了低通滤波器和陷波滤波器的相关概念、特性以及用法。

1 低通滤波器

运动控制器中最常用的滤波器是低通滤波器，理想低通滤波器在控制信号的频率分量低于截止频率时完全通过，而高于截止频率的频率分量完全阻断［3］。但理想特性低通滤波器实现困难，且信号在频域突然截断，会造成控制信号在时域的振荡。在实际使用中，常用低通滤波器如图1伯德图曲线所示，当控制信号频率值处于通带时，运动控制器幅值和相位无衰减通过;当高于截止频率时，幅值和相位将会逐渐衰减，且频率值越高衰减越大，通带与阻带之间有个过渡带。

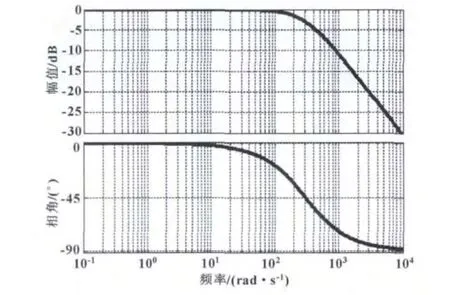
图1 常用的低通滤波器

在运动控制器中，运动控制系统控制信号频率不能任意取值，它受到设备机械结构及工况的限制，通常都处在一定的频率段，最大值也在千赫兹数量级。更高频率的控制信号一般是噪声、外界干扰或者电子元器件产生的辐射干扰，这些信号需要进行滤除，低通滤波器能够很好的完成这个任务［4－5］。另外根据信号的采用定理，当输入数字控制信号的频率超过运动控制系统的奈奎斯特频率时，会产生信号的混叠。混叠造成控制信号失真，不仅影响频率较高的控制信号分量，还会干扰到能够准确响应的较低频率的控制信号分量［3］。低通滤波器可以通过设置截止频率——一般为低于奈奎斯特频率值，来消除运动控制器中存在的频率混叠现象。同时低通滤波器对衰减高频噪声，抑制高频谐振也有明显的效果。

最简单的低通滤波器为一阶低通滤波器，如式(1)所示。

图2 截止频率相等时一阶和二阶低通滤波器伯德图

式中:ωn为低通滤波器的自然频率，ξ为滤波器的阻尼系数。

在实际低通滤波器应用中，一般不希望低通滤波器自身产生谐振现象，即某些频率分量幅值被急剧放大。一阶低通滤波器不存在这种现象，但二阶低通滤波器却存在，这是不希望发生的。实际上这是由于阻尼系数ξ的取值造成的。如图3所示，ξ分别取0、0.1、0.5、0.7、1.0，在伯德图中可以看到:幅值方面，ξ值很小时，滤波器会产生谐振，在谐振处会产生很大的超调，当ξ数值逐渐变大时，超调逐渐消失;相位方面，当ξ=0时，通带部分相位滞后几乎

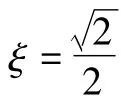
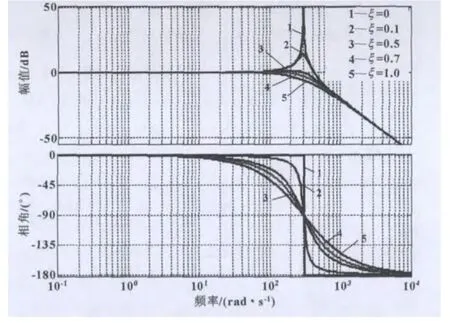
图3 阻尼系数ξ取不同值对应的伯德图

二阶低通滤波器伯德图如图2中虚线所示，与图2中的截止频率为300 rad/s的一阶低通滤波器曲线相比，可以发现:二阶低通滤波器在幅值衰减方面，作用明显好于一阶低通滤波器，但在相位图上可以看到，二阶低通滤波器引入的相位滞后值明显更大。这些特点使得在实际使用中，要综合考虑运动控制器的相位裕量和需要的实际带宽，进而选择合适的低通滤波器类型和参数。

2 陷波滤波器

陷波滤波器，也称为带阻滤波器。在控制系统中也有广泛的用途。控制系统在设计带宽范围内常有一些谐振点，这些谐振现象很多是控制器的固有属性，通过调整控制器的控制参数很难消除，或者消除之后运动控制器的控制带宽变小，控制特性变差，此时用陷波滤波器抑制谐振，平滑伯德图运动控制曲线效果良好。此外如果一些噪声和干扰源的频率分布是已知的，并且与运动控制器所处频率段不同，那么可以通过陷波滤波器来消除特定频率范围的干扰和噪声。抑制控制带宽内的谐振这一应用在实际工程中更多一

如要设计带宽为300 rad/s的二阶低通滤波器，则ωn=300 rad/s，ξ=0.7，对应的二阶低通滤波器表达式为式 (3)。些。

陷波滤波器的一种常用表达式为式 (4)所示［4］。

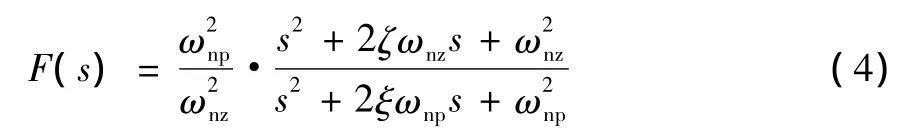
其中:ωnz为分子多项式的自然频率;ζ为分子多项式阻尼系数;ωnp为分母多项式自然频率;ξ分母多项式阻尼系数。其中，ωnz对应着衰减频率段的中心频率，ωnp则影响着陷波滤波器作用后的高频段特性。

如果ωnz和ωnp不同，此时有4个参数影响着陷波滤波器的性能，如ωnz为300 rad/s，ωnp为500 rad/s，ζ为0.017，ξ为0.10，所得陷波滤波器如图4。在低频部分，陷波滤波器不会产生放大或者衰减作用，在经过陷波滤波器作用过后的高频部分，陷波滤波器会根据ωnz和ωnp比例关系，产生相应的放大或者衰减作用，增益值G分贝值表达式如式 (5)。将参数代入式 (5)，计算得到本例中高频分量部分的增益值G为8.87 dB。

图4 ωnp=500 rad/s，ωnz=300 rad/s，ζ=0.017，ξ=0.1

图5 ωn=300 rad/s，B=100 rad/s，D= －20 dB

陷波滤波器一般利用其对特定频率段进行阻断衰减的特性，不会对高频分量进行处理，此时ωn=ωnz=ωnp，表达式变为式 (6)。

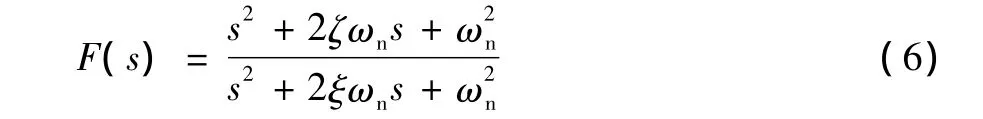
此时3个参数ωn、ζ和ξ决定陷波滤波器的性能。此时滤波器在衰减范围之外不改变运动控制器的幅值以及相位，并且可以近似认为2ξωn值对应着衰减到－3 dB幅值以下频率范围所对应的带宽B。ζ和ξ比值等于 ωn处衰减的幅值，其分贝值D按照式(7)计算，例如当比值为0.1时，D=－20 dB，即ωn处衰减20 dB。一陷波滤波器参数如下:ωn为300 rad/s，B为100 rad/s，D为－20 dB，所得滤波器如图5所示。

陷波滤波器的表达式也可以用通用形式，如式(8)。

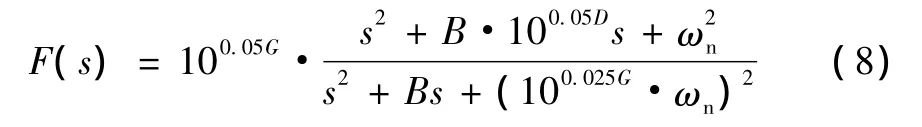
式中:ωn(=ωnz)是衰减频率段的中心频率;D为衰减频率段中心处衰减深度;G为陷波滤波器对高频响应增益分贝值;G值按式 (8)计算，由于陷波滤波器使用时G值不会很大，B近似为衰减频率范围的带宽。

由于运动控制器主要应用二阶低通滤波器对特定频率范围的阻断功能，所以在运动控制器中，陷波滤波器不对其作用后的高频分量进行衰减或放大，即G=0 dB。此时有3个参数ωn、B和D决定陷波滤波器性能。此时陷波滤波器表示为式 (9)。

如运动控制系统简化的传递函数为式 (10)，其对应的伯德图如图6所示。

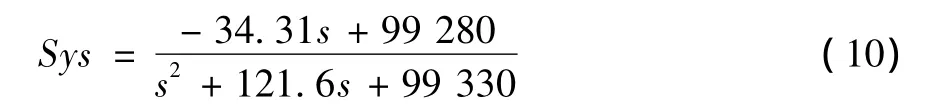
经观察，在150～400 rad/s频率范围内，系统出现了幅值增大的谐振现象，谐振峰值为8.5 dB，谐振中心频率为300 rad/s。这种控制系统伯德图中出现的谐振会给控制系统带来不稳定隐患，并降低的带宽B，常用的解决办法是加陷波滤波器［7－8］。通过分析，陷波滤波器参数为:ωn=300 rad/s，D=－8.5 dB，B=250 rad/s，表达式为式 (11)所示。

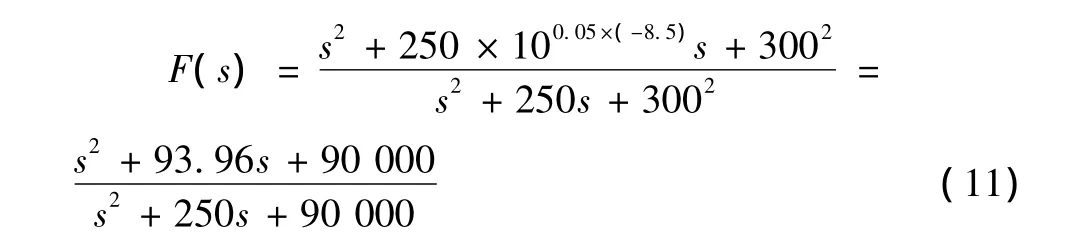
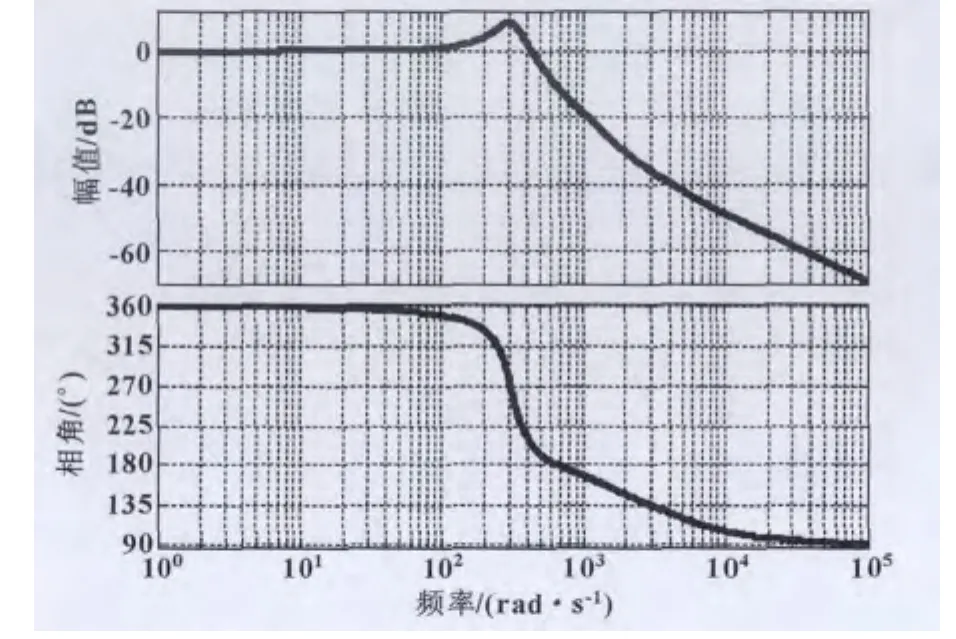
图6 系统未加滤波器时伯德图

式 (11)所得陷波滤波器伯德图如图7所示。控制系统中加入陷波滤波器后伯德图如图8所示。对比加入陷波滤波器前后可知，加入陷波滤波器后控制系统的谐振现象得到了明显的抑制，系统带宽B变大，实现了预期目标。

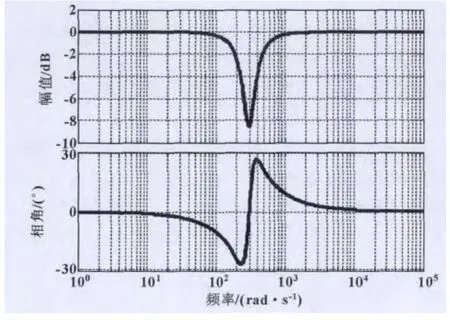
图7 ωn=300 rad/s，B=200 rad/s，D= －8 dB

图8 系统加陷波滤波器时伯德图

由于本例中系统谐振出现在系统带宽附近的高频段，故也可以用低通滤波器来实现，分别选取一阶和二阶低通滤波器截止频率均为200 rad/s，得到控制系统加入低通滤波器后伯德图如图9所示，也实现了预期目标。虽然陷波滤波器和低通滤波器都能满足此时的要求。但当带宽范围内出现谐振现象，就只能用陷波滤波器。对于多环控制运动控制器，如果一次调试效果不满足要求，可以重复调整滤波器参数，甚至可以根据每种滤波器的特点和控制环路要求使用组合滤波器，从而达到较好的幅值和相位特性［7－8］。

图9 系统加一阶和二阶低通滤波器伯德图

3 总结

滤波器在运动控制器中对改善控制器特性具有明显的效果，其实现形式有很多种，文中所选用的滤波器结构形式简单，容易实现，又贴近实际工程应用，基本能满足运动控制器需求［6］。其中，低通滤波器主要用于抑制高频噪声、干扰，衰减无用的高频控制信号，平滑运动控制曲线和抑制高频谐振;陷波滤波器通常用于处理系统中带宽范围内的谐振现象。在实际使用中，应该根据每种滤波器的特性选用。如果一种滤波器或者一个滤波器不能满足要求，可以使用组合滤波器。由于陷波滤波器与二阶低通滤波器形式相近，可以设计成通用形式，用户根据需要选择实际作用类型及相关参数。需要说明的是，在控制回路中引入滤波器相当于在控制系统中引入了延迟，这对控制系统的稳定性不利。因而使用滤波器并不是提升运动控制器性能优先考虑的选项，应先调整运动控制器的控制参数，在调整控制参数对控制效果改善不再明显的条件下，加入滤波器。对于多环运动控制器，先由内环向外环逐步调整控制参数，每个环路在调整参数后可以选择对应的滤波器，以使自身性能最佳，每个环路性能最佳进而能保证控制系统性能最佳［7－8］。在综合考虑滤波器与控制系统特性后，合理使用滤波器就能更好地发挥运动控制器性能。

［1］SIEMENS.SINUMERIK 802D sl/SINAMICS S120 Machine Data and Interface signals，Parameter Manual［M］.2005.

［2］FANUC.FANUC AC Servo Motor参数说明书［M］.2011.

［3］OPPENHIEM AlanV.WILLSKY Alan S.信号与系统［M］.刘树棠，译.西安:西安交通大学出版社，2009.

［4］ELLIS George.Control System Design Guide［M］.4th ed.美国:Butterworth-heinemann Publisher，2012.

［5］郭亮.数控机床动态特性优化研究［D］.西安:西安交通大学，2012.

［6］OGATH Katsuhiko.现代控制工程［M］.北京:电子工业出版社，2010:470－475.

［7］边江，马国春.西门子840D系统驱动优化详解［J］.金属加工(冷加工)，2009，583:(4).

［8］郭亮，梅雪松，张东升，等.840D数控系统的伺服参数优化［J］.机电工程，2011，28(4):444 －447.