伺服控制参数对摩擦误差影响的研究
2014-07-18牟恩旭冯斌任建功叶献斌
牟恩旭,冯斌,任建功,叶献斌
(西安交通大学机械工程学院,陕西西安710049)
摩擦是影响伺服控制系统精度的主要原因之一[1]。在摩擦的影响下,伺服控制系统在换向处会产生较大的误差尖峰,严重影响伺服系统的高速高精度控制。为了解决摩擦现象带来的问题,许多学者围绕摩擦模型及摩擦误差补偿进行了研究[2]。以下通过建立控制系统模型和摩擦模型,试图从时域和频域角度分析不同控制参数对伺服系统换向处摩擦误差的影响,从而为伺服控制系统参数设置及优化提供参考。
1 控制系统建模
文中采用的控制系统模型为基于PID控制结构的三环控制器,即该控制器由3个控制环组成。由内至外依次为电流环、速度环及位置环。在通常情况下,由于实际分析的频率范围较低,而其电流环往往有较高的带宽,故可以将电流环近似等效为一个比例环节。该比例环节的增益为Kt,其数值可以通过查询所使用的伺服电机手册得到。其速度环采用比例-积分控制器,位置环采用比例控制器。控制对象包括电机及其所连接的丝杠螺母、工作台等机械部分。
为获得更好的控制效果,减小跟随误差,加入了速度前馈的控制策略。为便于分析,将其机械部分等效为一个惯量阻尼系统,其数学模型为:

式中:T为电机产生扭矩;
J为系统机械部分等效惯量;
B为系统机械部分等效阻尼系数;
θ为系统转过角度。
通过对自主开发的开放式数控X-Y精密工作平台的X轴机械部分进行辨识,确定其机械部分等效惯量为0.003 kg·m2。通过查找使用的伺服电机手册确定Kt=2.687 5 N·m/V。
2 摩擦模型建模
在伺服控制系统实际运行时,摩擦是造成其在运动换向时误差过大的主要原因。因此,对摩擦模型的研究是相关领域中的热门之一。目前针对摩擦特性的研究成果很多,大致可将摩擦特性分为以下几个阶段[3]:
(1)静摩擦阶段。对于油脂润滑的固体接触面而言,静摩擦力幅值一般具有大于运动开始段的摩擦力幅值。当伺服系统运动方向发生换向时,会因为驱动力小而不能克服静摩擦力,而出现黏滑现象。在此阶段,虽然工作台仍有微动,但不明显,可以认为其静止。
(2)边界润滑阶段。此时运动部件的相对运动很低,无法形成润滑油膜,摩擦力实际上仍然是固体接触面的剪切作用,其大小主要由固体接触面的粗糙度来决定。
(3)部分润滑阶段。随着运动速度的加快,相对运动使接触表面间的液体油膜逐渐形成,但仍有部分区域为固体接触,因此这个阶段也被称为混合摩擦阶段。
(4)全流体润滑阶段。此时运动部件的相对运动速度继续增大,形成有效的液体油膜,此时的摩擦力主要表现了与相对运动速度相关的黏滞摩擦的作用。
采用ERKORKMAZ等人在文献 [4]中给出的模型,其具体方程如式 (2)所示:

式中:ω为系统运动角速度;T为系统指令力矩;

通过对自主研发的开放式X-Y精密工作平台X轴机械部分进行辨识,确定摩擦模型参数如表1所示。

表1 辨识结果
至此对控制系统及摩擦建模均已完成,由公式(2)可知,将系统黏性阻尼加至摩擦模型中一并考虑。图1给出模型的整体结构:
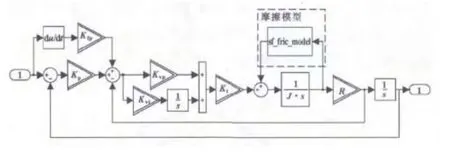
图1 系统整体模型

式中:l为丝杠导程。
3 控制系统参数对系统摩擦误差的影响
从以上可知,摩擦在系统换向时会造成很大的误差,因而对摩擦误差的补偿对实现系统高精度控制尤为重要[5]。通常摩擦补偿方法可以分为基于摩擦模型的补偿方法及基于摩擦补偿脉冲前馈的补偿方法。前者对摩擦模型的准确性要求较高,难以实现。故实际中如商用的数控系统西门子、法那科等均采用后者实现摩擦误差补偿。其原理即在系统进行换向时,向控制环路中加入补偿脉冲来对摩擦误差进行补偿[6]。补偿量的大小与摩擦误差的大小呈正比例关系。即当摩擦误差大时,所需要的补偿脉冲也大。而较大的补偿脉冲会对系统造成冲击,使系统产生振荡。通过分析控制系统参数对系统摩擦误差的影响,可以确定较为合理的参数,使系统换向处的误差减小,有利于摩擦补偿的稳定进行。
此外,通常对控制系统的分析,往往将注意力集
图1中:Kp为位置环比例增益;Kvp为速度环比例增益;Kvi为速度环积分增益;R为角度-位移转换系数,其值按如式 (3)确定:中于系统对指令的跟随情况,不重视系统对诸如摩擦之类的外界干扰的抑制能力。通过对控制系统各参数对系统摩擦误差的影响进行分析,可以为控制器参数的设计提供参考依据。下面从频域与时域两个方面对不同参数对系统摩擦误差的影响进行分析。
3.1 频域分析
由图1可知,系统在换向处所受到的摩擦力的突然变化可以看做外界的扰动[7],可知其传递函数为:
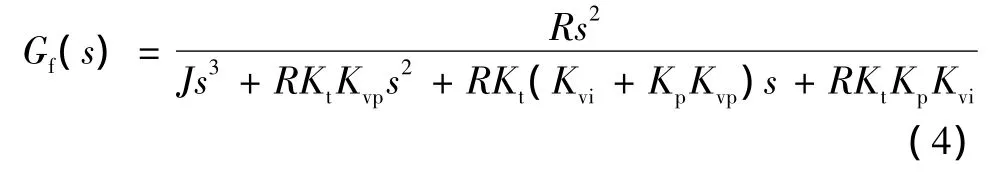
绘出传递函数Gf(s)在不同控制参数下的Bode图,如图2所示,从图上可以看出各参数对不同频段的影响。控制系统中的参数Kvp主要影响系统摩擦误差的中、高频成份;而Kvi,Kp主要影响系统摩擦误差中的中、低频成份,从频域上看,二者对系统摩擦误差的影响是相似的;系统的机械惯量J主要影响系统摩擦误差中的高频成份。
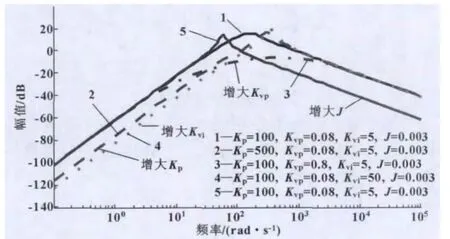
图2 不同参数下传递函数Gf(s)的bode图
3.2 时域分析

图3 换向处摩擦误差示意图
由于系统换向时的误差主要由摩擦现象造成,以下主要对该处误差进行分析。系统换向时误差的评价标准,为该处误差的尖峰值,以及在摩擦误差持续时间内,系统误差的绝对平均值。摩擦误差持续时间为从换向点处到系统误差经历峰值后趋于平稳的时间,如图3所示。
(1)位置环比例增益Kp对系统摩擦误差的影响
在确定速度环参数Kvp=0.08,Kvi=5不变情况下,在[90,290]范围内更改位置环比例增益Kp值。
由图4和图5可以看出,增大位置环比例增益Kp能够减小换向处摩擦误差尖峰值及其持续时间,同时可以减小摩擦误差平均值。但Kp的值在实际中并不能无限增大,过大的Kp值会导致系统振荡、不稳定。
(2)速度环比例增益Kvp对系统摩擦误差的影响
在确定位置环比例增益Kp=190,速度环积分增益Kvi=5不变情况下,在 [0.08,0.28]范围内更改速度环比例增益Kvp值。
由图6和图7可以看出,Kvp主要对减小换向处摩擦误差的峰值有效,对摩擦误差的持续时间影响较小。ELLIS[8]在文献中指出,对系统误差中、高频段的抑制会减小误差尖峰,对低频段的抑制会减小误差持续时间。因此,其时域上的分析结果同频域分析中“增大Kvp能够抑制摩擦误差中的中、高频成份”的结论是一致的。

图6 不同速度环比例增益对摩擦误差形态影响
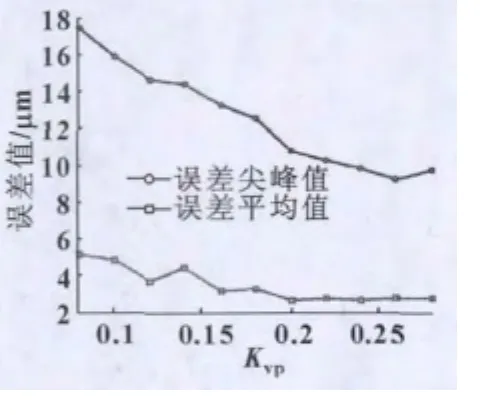
图7 速度环比例增益对摩擦误差影响
(3)速度环积分增益Kvi对系统摩擦误差的影响
在确定位置环比例增益Kp=190,速度环比例增益Kvp=0.08不变情况下,在 [1,11]范围内更改速度环积分增益Kvi值。
由图8和图9可以看出,增大Kvi能同时减小摩擦误差的峰值及持续时间,这与增大Kp有相似的效果,这与对二者的频域分析结果是一致的。增大Kvi值,可以降低摩擦误差峰值、缩短摩擦误差持续时间。但当Kvi增大到一定值的时候,摩擦误差曲线出现振荡,这种现象同系统在较大速度环积分增益时的阶跃响应超调及振荡现象类似。因此,为使系统能够更好地抑制摩擦误差且不产生振荡,应该选用合适的Kvi值。
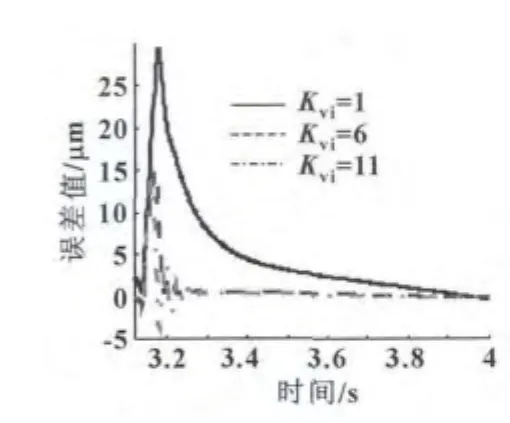
图8 不同速度环积分增益对摩擦误差形态影响
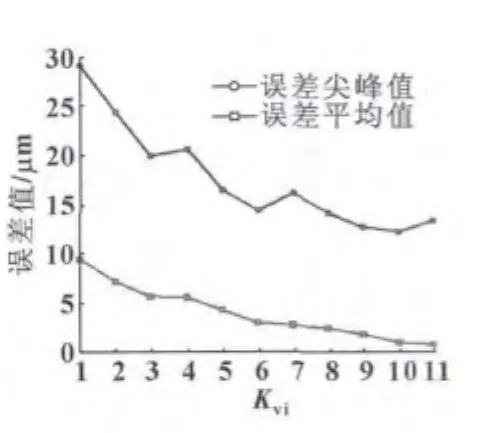
图9 速度环积分增益对摩擦误差影响
4 总结
通过在不同伺服控制参数下对系统换向点处摩擦误差的仿真,从时域和频域角度分析了各个参数对摩擦误差形态及有关评价指标的影响。通过分析可以发现,控制参数中的位置环比例增益Kp和速度环积分增益Kvi主要抑制摩擦误差中的中、低频成份。通过适当增大这两个参数,可以减小摩擦误差峰值和摩擦误差持续时间。而速度环比例增益Kvp主要抑制摩擦误差中的中、高频成份。通过增大Kvp,可以有效降低摩擦误差峰值,但对摩擦误差持续时间影响较小。因而,在无摩擦补偿的条件下,适当调整控制系统参数,可以减小摩擦误差,有利于后续进行的摩擦补偿的实现。由于控制系统参数对系统的摩擦误差有着直接的影响,可以将伺服系统在换向点处的摩擦误差作为评价伺服系统性能的指标之一,指导伺服系统控制参数的调整与优化。
[1]XUESONG M,TSUTSUMI M,TAO T,et al.Study on the Compensation of Error by Stick-slip for High-Precision Table[J].International Journal of Machine Tools & Manufacture,2004,44(5):503-510.
[2]ARMSTRONG-HÉLOUVRY B,DUPONT P,DE WIT CC.A Survey of Models,Analysis Tools and Compensation Methods for the Control of Machines with Friction[J].Automatica,1994,30(7):1083-1138.
[3]OLSSON H,ÅSTÖM KJ,CANUDAS dE WIT C,et al.Friction Models and Friction Compensation[J].European Journal of Control,1998(4):176-195.
[4]ERKORKMAZ K,ALTINTAS Y.High speed CNC System Design.Part II:Modeling and Identification of Feed Drives[J].International Journal of Machine Tools & Manufacture,2001,41(10):1487-1509.
[5]冯斌,张东升,程有龙,等.开放式数控系统摩擦补偿的实现[J].机床与液压,2011,39(19):7-9.
[6]陈广胜,梅雪松,陶涛(2011).X-Y工作台摩擦误差补偿方法的研究[J].西安交通大学学报,2011,45(1):69-73.
[7]刘栋.数控机床伺服进给系统建模、辨识及精密控制研究[D]:西安:西安交通大学,2010.
[8]ELLIS G.Control System Design Guide[M].San Diego:Elsevier Academic Press,2004.
