高精度无心磨削圆度保证和成圆过程解析

崔奇，丁辉，程凯

(哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001)

无心磨削作为一种高效的精密加工方法，广泛应用于汽车和轴承等行业，特别适合于需对回转表面进行精密加工的轴套类零件的大批量生产，如轴承滚子、轴承圈、气门芯阀、凸轮轴和曲柄轴等。无心磨削滚子的圆度误差可达0.1～0.3 μm，贯穿磨削时效率可达250～350件/min［1］。无心磨削可以对工件的外圆表面、内圆表面和圆锥表面等进行加工，常用的加工方式有贯穿磨削和切入磨削。

无心磨削精度的主要内容是圆度误差，需要对成圆机制和成圆稳定性进行研究，很多学者进行了相关的工作［2－5］。ROWE 等［6－8］对成圆机制进行了研究，分析了各环节对加工精度的影响，给出了稳定性的计算方法和稳定性图。GARITAONANDIA等［9－10］对动态稳定性进行了研究，使用根轨迹法求解特征方程，利用有限元模型得到机床的动态模型。HASHIMOTO等［11－12］研究了工件转速和磨削角对磨削振动的影响，并考虑了磨削干涉的效应。无心磨削稳定性研究是在频域内对特定次数的谐波圆度误差进行研究，对圆度误差的预测则需要在时域内进行。对成圆过程的时域分析一般将磨削系统以单自由度或多自由度系统处理［13－14］。由于无心磨削圆度误差的影响因素多，各环节包含的非线性因素多，因此在稳定性分析中难以进行解析，但是可以对一定条件下的稳定性情况进行定性的预测。在时域分析中可以将较多的非线性计算在内，并使用数值计算方法进行圆度误差的预测，但是需要对磨削系统进行合理的处理，以节约计算成本。

文中对无心磨削的成圆过程进行分析，讨论圆度误差的主要影响环节并有针对性地给出相应的改进策略。通过分析磨削系统各环节与工件之间的作用过程，在时域内对工件成圆过程进行解析和仿真，对圆度误差进行预测。

1 高精度无心磨削圆度误差保证方法

1.1 无心外圆磨削成圆机制

无心磨削过程中，托板支撑工件，导轮带动工件旋转，多数情况下导轮架带动工件和托板一同向砂轮径向运动以实现进给。普通定中心磨削时工件的位置主要由主轴回转运动和工件变形等确定，而在无心磨削过程中，工件与导轮和托板的接触位置等因素决定了砂轮对工件的磨削区域，因此对成圆过程的研究可以归结为确定砂轮和工件之间的相对位置，而这一位置又是主要由工件与托板和导轮之间的相对位置决定的。

(1)几何成圆机制

几何成圆机制从几何关系的角度出发分析磨削过程中工件与砂轮、导轮和托板之间的相互位置关系，而没有考虑磨削力和机床刚度等因素对成圆过程的影响。更准确地说几何成圆机制所完成的工作主要是几何关系分析，而这一分析是成圆过程分析的基础。

如图1所示，设砂轮、导轮和工件直径分别为ds、dc和dw，托板倾角和磨削角分别为γ和β，其他几何关系可以通过这些基本参数计算获得。

图1 无心磨削运动关系

将工件的初始理想半径记为R，磨削过程中工件转过的角度为θ，此即为工件已磨削的圆周的角度，对应于此角度处的工件的实际半径记为r(θ)，相对于工件初始理想半径的减少量为Δr(θ)，即:

Δr(θ)的值也是砂轮磨削点与工件理想轮廓的距离，因此点B和点C的工件半径减少量分别可表示为Δr(θ－α)和Δr(θ－π+β)，当砂轮在工件半径方向的进给为X(θ)时，Δr(θ)可以表示为:

其中:K1和K2是与几何角度相关的参数，可以通过数学关系分析得到:

从式 (3)和 (4)可以看出:K2一般比K1大许多，也就是说工件与导轮接触点的误差将会以更大的比例影响工件与砂轮之间的位置关系，进而影响工件的成圆和圆度误差。K2的最大值为1，此时的磨削角β为0，此时工件在导轮处的误差将会完全反映到磨削点，托板的作用仅是支撑工件而对成圆不起作用，工件表面的偶数次谐波误差可以有效地减小，奇数次谐波误差无法消除。

(2)静态成圆机制

静态成圆机制在研究成圆过程时简化处理无心磨削过程中的动态特性，将磨削过程中的变形以静态变形的形式来处理，使用磨削刚度KG和磨削系统的刚度KM来计算在磨削深度为ap时所产生的法向磨削力Fn和工件磨削点法向上的变形δN:

将上述关系引入式 (2)中，成圆方程可以表示为:

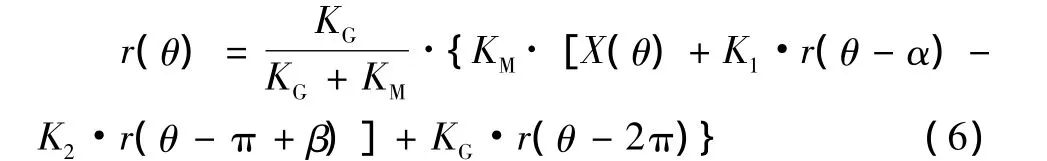
(3)动态成圆机制

动态成圆机制是在考虑机床动态特性的基础上，将由于这一特性引起的变形引入成圆方程中:

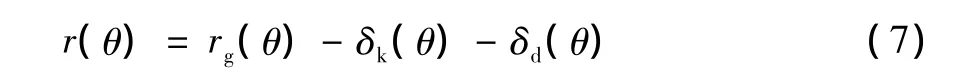
其中:rg(θ)、δk(θ)、δd(θ)分别为机床的几何位移关系、静态变形和动态变形。rg(θ)可以表示为式 (2)中等号的右边，δk(θ)和δd(θ)也可以合并为一个完整的动态项。

在动态成圆机制的研究过程中，使用较多的方法的是将系统简化为单自由度或二自由度二阶系统，并且忽略其中的非线性因素，与实验所得的试件外圆轮廓相比，仿真所得到的结果一般可以定性地表示成圆的趋势，但如要实现较为准确的外圆轮廓预测还有一定的差距。

1.2 无心磨削的稳定性

稳定性分析的内容是对工件圆周各次谐波误差的增长率进行分析，以保证工件在经过每一周的磨削后相应次数的误差被有效地消除。分析时一般对成圆方程进行Laplace变换，转化至频域对各次谐波误差的稳定性情况进行计算。将前一节中的成圆方程转化至频域后工件圆周第n次谐波误差的稳定性参数为［8］:

上述参数In即为在一定的磨削角和托板倾角的条件下每经过一周的磨削第n次圆度误差的消除参数，当大于0时表示误差减小，否则表示此时对第n次圆度误差没有成圆效果。

稳定性对圆度误差的影响较大，磨削过程中应避免在稳定性低的区域工作，尤其是对于低次谐波圆度误差，由于低次误差相比于高次误差更难消除，并且高次误差由于砂轮磨削时的滤波效应而难以增长，所以应合理选择磨削工艺参数使尽可能多的低次谐波误差具有尽量高的稳定性参数。

1.3 砂轮和导轮

砂轮和导轮直接影响工件的被磨削区域，对工件表面的成圆过程影响较大。砂轮转速较高，首先需要较好的平衡，工作时需要有较好的回转精度，对轴承的要求较高。国内传统的通用无心磨床砂轮主轴多为液体动压轴承，轴承的回转精度和刚度受轴瓦加工、刮研、装配和调整等的影响较大，尤其是在批量生产中难以稳定地保证较高的工作精度。使用动压轴承的导轮主轴通常是机床刚度链中柔性最大的环节，如果调整不当加工精度将难以保证。

使用高精度滚动主轴轴承的砂轮主轴和导轮主轴可以有效地解决上述问题，其回转精度、刚度在得到保证的同时热稳定性等也有所改善。

与砂轮和导轮相关的另一个重要内容是它们的修整问题。砂轮轮廓母线一般为直母线或分段直母线，主要受修整器运动精度的影响。由于导轮轴线在水平面内回转倾斜一定角度，使其理想轮廓变得复杂，修整时使用单点刀具可得到与之近似的双曲面，需要使用滚轮修整才可以加工出理想的轮廓表面。

2 无心磨削成圆过程解析

2.1 工件位置的确定

无心磨削成圆过程解析首先应确定工件与砂轮的相对位置，以准确计算工件表面的被磨削状态。为此，首先应准确计算工件与托板导轮的接触位置和相对应的工件的位移。计算工件与托板接触位置的方法如图2所示:在时刻t工件转过的角度为θ时，工件与托板的理论接触点为点P，由于工件表面轮廓误差的存在，使实际接触点为点P'，此时OPOP'的夹角为θP，P'的工件半径为r(θ－θP)，对应的工件圆心与托板的距离为:

图2 工件与托板接触关系

计算实际接触点时，使搜索角度θP在理论接触点附近角度范围为 (－φ，+φ)的区域内变化，以工件中心距离托板最大者作为实际值。工件与导轮接触位置的计算与此类似。

2.2 成圆过程的时域解析

在时域内对成圆过程进行解析可以对圆度误差进行预测，通过对磨削前后圆度误差的对比完成对各阶次圆度误差稳定性和消除能力的分析，这一过程使用前文所述的成圆方程进行计算。在稳定磨削状态下，工件与导轮之间没有相对滑动，工件被磨削的时间t与转过的角度θ有准确的对应关系:

式中:ωw为工件角速度。

使用成圆方程进行时域解析过程中，对磨削过程存在的非线性环节需要有效处理。主要包括:

(1)工件位置关系。计算工件位置时应根据工件、砂轮、托板和导轮的轮廓形状计算工件与它们的接触和干涉区域。

(2)磨削区域干涉效应。这一效应使得磨削区域、磨削力和变形等受到工件实时轮廓的影响。

(3)材料去除条件。即在使用成圆方程计算时，任一时刻工件每一位置的半径值不能大于上一时刻该位置的半径值。

2.3 成圆过程的仿真

在得到工件成圆方程后可以在时域内对成圆过程进行仿真，对圆度误差进行预测。仿真过程中首先输入磨削过程的工艺参数和工件初始轮廓，将工件圆周离散成若干份 (如3 600等分)，之后按每一等分所对应的时间步长递增，使用成圆方程离散计算每一离散时刻工件在磨削区域半径的变化情况，直至磨削过程终点。在得到工件磨削后圆周各点半径后，可以使用最小二乘法等方法计算工件的圆度误差。仿真过程中，由于非线性因素对成圆过程和圆度误差的重要影响，把前文所述的非线性环节计算在内。

3 实验验证

实验在一台通用无心外圆磨床上进行，砂轮主轴为双支撑悬臂结构，两轴承为可倾瓦式液体动压径向轴承，导轮主轴结构与砂轮类似，两径向轴承为圆柱滑动轴承。砂轮主轴和导轮主轴轴承的刚度较低，相应方向的刚度主要与它们有较大的关系。砂轮型号为P-500×150×305-A60K5V-35，导轮型号为 PSA-300×150×127-A80P0R-35。工件材料为未淬火45钢。实验时使用的磨削参数如表1所示。

表1 磨削条件

实验时使用的磨削方式为快速切入磨削，导轮架和托板带动工件一起向砂轮径向运动，并直接进给至行程终点，随后进入无进给光磨阶段，控制光磨圈数完成磨削循环，如图3所示。实验时使用的工件的初始形貌为在工件外圆表面沿整个轴向有一深度为18 μm平面，这时这一平面所代表的初始圆度误差占主导，可以使用傅里叶变换得到此时工件各阶次圆度误差的幅值，同工件磨削后的圆度误差对比计算得到各阶次圆度误差的消除情况和对应稳定性，对成圆情况进行分析。

图3 磨削实验

仿真预测和实际工件的外圆形貌如图4所示，可以看出:仿真得到的工件外圆轮廓与实验结果一致，实验测得的圆度误差为14.97 μm，仿真得到的圆度误差为12.98 μm，误差为13.3%。预测的误差值与实验值接近，出现误差的原因是工件实际轮廓上除了深度为18 μm平面外，在其他位置还存在误差，磨削过程砂轮和导轮的轮廓也存在误差，这些因素对最终结果都有影响。因此可看文中的解析方法可以有效地对工件的成圆过程进行预测。在得到工件的轮廓数据后，可以进一步计算各阶次误差的变化、磨削参数和机床参数等对各阶次误差消除能力的影响。

图4 工件轮廓

4 结论

无心磨削中精度要求的主要内容是获得低的圆度误差值，文中给出了影响圆度误差的关键环节的控制方法。借助稳定性分析选择合理的托板倾角和磨削角，尤其要避免低次不稳定谐波的出现。砂轮轮廓，特别是导轮理想轮廓要使用正确的修整方法来获得。砂轮和导轮主轴应有合理的结构和足够的刚度以减小自身振动对工件圆度误差的影响。

工件的成圆过程是工件与砂轮、托板和导轮作用下在磨削区域的动态过程。文中依据工件的轮廓来确定工件的运动状态和工件与砂轮、托板、导轮之间的解析关系，实时计算工件的成圆情况，对工件的成圆趋势进行预测。仿真和实验结果显示:该解析方法可以对工件的成圆情况进行准确的预测，计算误差消除能力和分析磨削参数对成圆过程的影响。

［1］HASHIMOTO F，GALLEGO I，OLIVEIRA J F G，et al.Ad

vances in Centerless Grinding Technol-ogy［J］.CIRP Annals-Manufacturing Technology，2012，61(2):747 －770.［2］LI Hongqi，SHIN Yung C.A Time Domain Dynamic Simulation Model for Stability Prediction of Infeed Centerless Grinding Processes［J］.Journal of Manu-facturing Science and Engineering，2007，129(3):539 －551.

［3］BARRENETXEA D，ALVAREZ J，MADARIAGA J，et al.Stability Analysis and Time Domain Simula-tion of Multiple Diameter Parts during Infeed Cen-terless Grinding［J］.CIRP Annals-Manufacturing Technology，2011，60(1):351－354.

［4］BUENO R，ZATARAIN M，AGUINAGALDE J M，et al.Geometric and Dynamic Stability in Centerless Grinding［J］.Annals of the CIRP，1990，39(1):395 －398.

［5］LIZARRALDE R，BARRENETXEA D，GALLEGO I，et al.Practical Application of New Simulation Methods for Elimination of Geometric Instabilities in Centerless Grinding［J］.Annals of the CIRP，2005，54(1):273 －276.

［6］ROWE W B，RICHARDS D L.Research Note:Geometric Stability Charts for the Centreless Grind-ing Process［J］.Journal of Mechanical Engineering Science，1972，14(2):155－160.

［7］ROWE W B，MIYASHITA M，KOENIG W.Centerless Grinding Research and Its Application in Advanced Manufacturing Technology［J］.Annals of the CIRP，1989，38(2):1－9.

［8］MARINESCU Ioan D，HITCHINER Mike P，UHLMANN Eckart，et al.Handbook of Machining with Grinding Wheels［M］.Boca Raton:CRC Press，2007:479 －548.

［9］GARITAONANDIA I，FERNANDESA M H，AL-BIZURI J.Dynamic Model of a Centerless Grinding Machine Based on an Updated FE Model［J］.International Journal of Machine Tools and Manufacture，2008，48(7/8):832 －840.

［10］GARITAONANDIA I，FERNANDES M H，ALBIZURI J，et al.A New Perspective on the Stability Study of Centerless Grinding Process［J］.International Journal of Machine Tools and Manufacture，2010，50(2):165 －173.

［11］HASHIMOTO F，LAHOTI G D，MIYASHITA M.Safe Operations and Friction Characteristics ofRegulation Wheel in Centerless Grinding［J］.CIRP Annals-Manufacturing Technology，1998，47(1):281 －286.

［12］HASHIMOTO F，ZHOU S S，LAHOTI G D，et al.Stability Diagram for Chatter Free Centerless Grinding and its Application in Machine Development［J］.CIRP Annals-Manufacturing Technology，2000，49(1):225 －230.

［13］CHIEN A Y.The Harmonic Vibration Models in Centerless Grinding［J］.International Journal of Machine Tool Design and Research，1986，26(4):349－358.

［14］JAMESON J R，FARRIS T N，CHANDRASEKAR S.Equilibrium and Compatibility Simulation of Plunge Centreless Grinding［J］.Proceedings of the Institution of Mechanical Engineers:Part B:Journal of Engineering Manufacture，2008，222(7):747 －757.