基于分区模型的城市供水管网压力监测点布置

何忠华，袁一星

（1.哈尔滨工业大学市政环境工程学院，150090哈尔滨；2.安徽工业大学建筑工程学院，243032安徽马鞍山）

基于分区模型的城市供水管网压力监测点布置

何忠华1，2，袁一星1

（1.哈尔滨工业大学市政环境工程学院，150090哈尔滨；2.安徽工业大学建筑工程学院，243032安徽马鞍山）

为掌握整个城市供水管网的压力分布情况，提出基于供水管网分区模型的压力监测点布置方法.首先采用欧氏距离度量供水管网中任意两两节点在一个运行周期内水压波动的相似度；然后按照给定的分区内最大允许欧氏距离限定要求，依次对每根管段上两个端节点的子区归属进行判断，从而实现对管网的分区；最后在各子区内选择一个最能代表本子区节点水压波动情况的节点作为压力监测点.将该分区布置模型应用于东北某市开发区的供水管网，分区结果表明，各子区内的所有节点是连通的，任意两两节点间的欧氏距离均在给定的最大允许值范围内，并且不同的最大允许欧氏距离形成不同精度的分区方案.在各子区内布置一个压力监测点，当压力监测点布置数目为4时，平均相对误差为4.53%，此时基本能反映供水管网的压力分布情况.

供水管网；压力监测点；分区模型；欧氏距离

实时掌握管网水压分布情况对于实施优化调度［1-2］、控制管网漏失［3-4］、降低爆管事故发生率及供水能耗具有重要意义［5-6］.为实时掌握供水管网水压的分布情况，需在管网中布置一定数目的压力监测点.目前，关于供水管网压力监测点的布置方法主要有敏感度分析法［7-9］、聚类分析法［10］、遗传算法寻址法［11］和相关性分析选址法［12］等.这些方法在实际工程中得到了一定的应用，但仍存在一些问题:压力监测点布置数目的多少普遍是人为指定的，未建立起监测点布置数目与监测精度之间的关系；节点聚类的依据仅仅是各节点水压在数字大小上的相似程度，未考虑节点在管网中的区域属性，导致聚类后归属同一类的节点可能是散布在管网不同位置上的节点，而不是构成一片区域的节点集，因而难以有效反映管网压力的区域分布情况并有效指导优化调度；基于节点流量摄动的水压敏感度分析法在流量摄动值的设定上显然带有主观性，而且敏感度分析是基于单工况分析的，未考虑延时工况，不能反映实际管网中的水压波动情况；遗传算法寻址法搜索空间巨大，计算费时，也可能搜寻不到最优解.为此，以东北某市开发区供水管网为例，尝试构建充分考虑节点区域属性和延时工况的分区模型，在分区的基础上进行压力监测点的布置，并建立监测点布置数目与监测精度的关系.

1 供水管网分区模型

1.1 欧氏距离

要全面准确地掌握整个供水管网的压力分布情况，客观上要求在每个用户节点均布置测压点.考虑到现代城市供水管网系统的规模，这种布置方案在投资和运行费用上均相当可观［13］.因此，在满足管网压力监测精度及经济要求的前提下，选用尽可能少、有代表性的节点作为压力监测点以获取整个城市供水管网的压力状况尤为重要［14］.“有代表性”节点的选择必须先对管网中所有节点根据其水压波动的相似度进行分区，将压力变化相似的节点划为同一个子区，再从子区中选择一个最能够代表本区压力波动的节点作为监测点，监测点的压力值反映子区内所有节点的压力值.“相似性”的度量一般采用欧氏距离［15］.假设供水管网中各节点在一个水力运行周期T内的水压数据可表示为

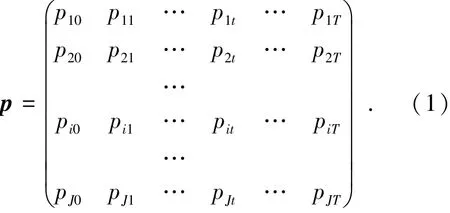
i=1，2，…，J；t=1，2，…，T，J为管网中的节点总数，节点i与节点j的欧氏距离可表示为

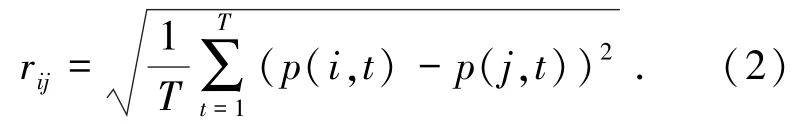
式中:rij为节点i与节点j的欧氏距离，反映了节点i与节点j水压波动的相似程度．rij越小，说明节点i与j的水压波动越相似，被化为同一个子区的可能性也越大．

1.2 分区算法

分区模型的计算流程如图1所示，主要计算步骤如下:

图1 分区模型计算流程

1）数据准备:①子区内节点间的最大允许欧氏距离值ε；②分区后的结果存放在矩阵District中，该矩阵是J×J型，每一行代表一个子区．

2）按照管段的编号顺序，从管段1开始搜索，直到搜索完管网中所有管段为止.

3）对于管网中的任一管段k，其对应的端节点为i和j．当搜索到管段k时，先判断节点i是否已被划分到某个子区内（即节点i是否已在矩阵District的某一行内）.如果节点i已被划分到某一个子区内，转到步骤4），否则节点i自成一个新的子区（即将节点i赋给矩阵District中的一个新行）.

4）判断节点j是否已被划分到某个子区内:①如果“否”，则先找出节点i在矩阵District中所在的子区（行），然后判断节点j与节点i所在子区（行）中所有节点之间的欧氏距离是否均满足小于ε．如果“否”，节点j自成一个新的子区（行）；如果“是”，则将节点j加入到节点i所在的子区（行）中．②如果“是”，则先找出节点j在矩阵District中所在的子区（行），然后判断节点j所在子区（行）中的每个节点同节点i所在子区（行）中所有节点之间的欧氏距离是否均小于ε．如果“是”，则将节点i所在的子区（行）和节点j所在的子区（行）合并成一个子区（行）；如果“否”则转到步骤5）．

5）对管段k+1依次按照步骤3）和4）进行分区，直至进行到NP根管段被划分完毕为止.

6）输出分区的结果矩阵District.

1.3 子区内压力监测点的确定

供水管网经过分区后，在每个子区内选择一个最具代表性的节点作为本子区的压力监测点.在一个水力运行周期内，对于一个包含n个节点的子区，与其余n-1个节点平均欧氏距离最小的节点，其水压波动情况也最能反映该子区内各节点的水压波动情况，即将其定为该子区的压力监测点．因此，使得平均欧氏距离取最小值的节点i即为该子区压力监测点的布置位置，即

此外，在子区内选择监测点时，也须适当兼顾管网中的一些特殊点，如水压最不利点、大用户点、供水分界线、管网末梢以及加压泵站前后等水压控制点或水压变化敏感点.对于不包含特殊点的子区，按照最小平均欧氏距离值选择压力监测点；对于仅包含两个普通节点的子区，选择第一个节点作为压力监测点；对于包含一个特殊点的子区，直接将其指定为该子区的压力监测点；对于包含多个特殊点的子区，则按照最小平均欧氏距离值择优选择特殊点.总之，各子区内压力监测点的布置需综合考虑理论计算结果、特殊节点、监测点施工的可行性以及工程需求等因素和约束.

2 算 例

2.1 工程概况

研究案例为东北某市开发区的供水管网，服务面积为17 km2，日用水量为5.2万m3／d，用水量变化曲线如图2所示.根据管网简化原则对该管网进行简化，结果如图3所示.

图2 城市用水量变化

图3 某市开发区供水管网拓扑结构

该供水管网管道总长约42.2 km，由38个用户节点、61根管段、1个水源和1个高位水池组成.由于管网铺设广、深埋于地下且受干扰因素多等原因，运营维护管理工作难度较大，管道泄漏和爆裂等事故屡屡发生，严重影响人民的正常生产和生活.为保证供水管网安全运营，须在管网中布置一定数目的水压监测点.通过及时掌握管网的水压分布情况，可以有针对性地进行优化调度，维持科学合理的水压分布，降低能耗，保证管网运营的经济性.同时也便于建立起降低供水管网漏损率和爆管率、保障管网正常运营的安全管理模式，为开展针对管网运营安全和预防事故发生的运营调度模式研究和开发提供依据.

要实现以上目标、获取有价值的水压数据，水压监测点的布置是关键.供水管网中压力监测点布置主要包括确定压力监测点布置数目、每一压力监测点所代表的子区和监测点的布置位置等3方面的内容.本文针对这3项内容，在现有研究的基础上进一步研究考虑延时工况、监测点布置数目和监测精度的压力监测点布置方法.

2.2 分区结果及分析

分区前先设定一些参数，一个水力运行周期T取24 h，ε的变化步长取0.01.

通过计算，分区数目N与子区内最大允许欧氏距离ε的变化关系如图4所示．可以看出，供水管网分区数目随子区内最大允许欧氏距离的增大而减小.子区内最大允许欧氏距离越小，分区及监测点数目越多，监测精度也就越高，但投资也大；反之则分区及监测点数目越少，精度越低，投资也小.

图4 分区数目与子区内最大允许欧氏距离

2.3 监测点布置结果及分析

当各子区内最大允许欧氏距离取7.37，8.63，11.5和15.26时，供水管网分别可分为5，4，3和2个子区，分区结果及监测点的布置位置如图5所示.可以看出，被划分在同一个子区内的节点在子区是有管段连通的节点集，也是集中分布在管网中某个区域的节点集，说明提出的分区模型确实反映了节点的区域属性.

图5 分区及监测点布置结果

为检验压力监测点布置的准确性，以平均相对误差度量监测精度，并定义为

表1 不同监测点数目下的相对误差

在不同分区数或监测点数目下，各节点和整个供水管网在一个运行周期内的平均相对误差如图6所示.由图6（a）可知，分区数为2和3的曲线部分重合，这是由于两者有一个相同的监测点25.大体上看，随着分区数目的增加，各节点的相对误差下降.由图6（b）可知，不同分区数目下供水管网水压的平均相对误差曲线均与用户的用水量变化曲线相似，在用水高峰的9时和18时，误差均比较大.这是因为在用水量较大时，管网中各管段的流量大，水头损失也大，导致各子区内节点的水压值差别也大，从而降低了监测点水压的代表性，误差增大.但随着分区数的增加，监测点布置数目增多，管网的平均相对误差下降.

从表1可以看出，当监测点布置数目从4增加到5后，平均相对误差降低甚微，但投资会显著增加.结合图5可知，当压力监测点布置数目为4时，监测点分布均匀，最不利点和管网末梢点等特殊位置均布有监测点，平均相对误差为4.53%，此时基本能反映整个供水管网的压力分布情况.

图6 不同分区数目N下的平均相对误差

3 结 论

1）提出了基于供水管网分区模型的测压点布置方法，以管段为搜索对象，依次判断各管段上两个节点的监测子区归属情况，最终将整个供水管网划分成若干个监测子区.

2）该法全面考虑了各节点在一个水力运行周期内的水压波动情况，而不是以单一工况下的水压数据为布置依据.

3）该法具有“多目标”布置的思想，无需事先给定监测点数目和精度，求解后会得到不同精度、不同测压点数目下的节点分区结果.在分区的基础上进行压力监测点的布置并建立了监测点布置数目与监测精度的关系，从而为压力监测点的布置提供多组规划方案.

4）根据管段的编号逐个将节点分区，有效地保证了各子区内所有节点在管网中是连通的.

5）该算法性能稳定，根据编号从小到大搜索，不存在因初始计算节点的不同影响收敛速度的问题.

6）该法用于测压点布置合理可行，计算效率高，代表性强，适用性好，能准确反映供水管网的压力分布情况，增强了水压管理的科学性.

［1］GIUSTOLISI O，LAUCELLI D，BERARDI L.Operational optimization:water losses versus energy costs［J］.Journal of Hydrauli Engineering，2013，139（4）:410-423.

｀［2］GIACOMELLO C，KAPELAN Z，NICOLINI M.Fast hybridoptimizationmethodforeffectivepump scheduling［J］.Journal of Water Resources Planning and Management，2013，139（2）:175-183.

［3］WU Z Y，SAGE P，TURTLE D.Pressure dependent leak detection model and its application to a district water system［J］.Journal of Water Resources Planning and Management，2010，136（1）:116-128.

［4］董深，吕谋，盛泽斌，等.基于遗传算法的供水管网反问题漏失定位［J］.哈尔滨工业大学学报，2013，45（2）:106-110.

［5］MOUNCE S R，BOXALL J B，MACHELL J.Development and verification of an online artificial intelligence system for detection of bursts and other abnormal flows［J］. Journal of Water Resources Planning and Management，2010，136（3）:309-318.

［6］GIRARD M，STEWART R A.Implementation of pressure and leakage management strategies on the gold coast，Australia:case study［J］.Journal of Water Resources Planning and Management，2007，133（3）:210-217.

［7］KANG D，LANSEY K.Novel approach to detecting pipe bursts in water distribution networks［J］.Journal of Water Resources Planning and Management，2014，140（1）:121-127.

［8］陆仁强，张宏伟，牛志广.基于非线性映射理论的城市供水管网压力监测点布置方法研究［J］.水利学报，2010，41（1）:25-29.

［9］刘书明，王欢欢，徐鹏，等.多目标大规模供水管网监测点的优化选址［J］.清华大学学报，2013，53（1）: 78-83.

［10］黄廷林，丛海兵.给水管网测压点优化布置的模糊聚类法［J］.中国给水排水，2001，17（11）:50-52.

［11］王伟哲，郄志红，刘美侠，等.基于改进遗传算法的供水管网故障监测点布置优化［J］.水力发电学报，2012，31（1）:15-19.

［12］郭思元，刘遂庆，陈嵘.给水管网压力监测点的优化布置［J］.中国给水排水，2004，20（12）:82-84.

［13］OSTFELD A，SALOMONS E.Optimal layout of early warning detection stations for water distribution systems security［J］.Journal of Water Resources Planning and Management，2004，130（5）:377-385.

［14］FARLEY B，MOUNCE S R，BOXALL J B.Development and field validation of a burst localization methodology［J］.JournalofWaterResourcesPlanningand Management，2013，139（6）:604-613.

［15］ISOVITSCH S L，VANBRIESEN J M.Sensor placement and optimizationcriteriadependenciesinawater distribution system［J］.Journal of Water Resources Planning and Management，2008，134（2）:186-196.

（编辑 刘 彤）

Layout of pressure monitoring points in urban water distribution system based on district model

HE Zhonghua1，2，YUAN Yixing1
（1.School of Municipal and Environmental Engineering，Harbin Institute of Technology，150090 Harbin，China；2.School of Civil Engineering and Architecture，Anhui University of Technology，243032 Ma＇anshan，Anhui，China）

To monitor the pressure distribution in urban water distribution system（WDS），a method of locating pressure monitoring points is proposed based on district model of WDS.First，Euclidean distance is introduced to measure the pressure fluctuation similarity between two nodes within a running cycle.Whether a node in a pipe is classified as one sub-district depends on that the Euclidean distance values between the node and other nodes of this sub-district is within a given maximum allowable Euclidean distance.Finally，a node with minimum average Euclidean distance in a sub-district is chosen as its pressure monitoring point location. This district method is applied to monitoring point layout of a practical WDS.The analysis results show that different district solutions are obtained by changing the maximum allowable Euclidean distance.All the nodes in each sub-district are connected and the Euclidean distance between any two nodes is within a given maximum allowable value.After placing one pressure monitoring point in each sub-district，the results show that the pressure distribution in WDS can be effectively reflected，when average relative error is 4.53%and the number of pressure monitoring point is four.

water distribution system；pressure monitoring points；district model；Euclidean distance

TU991.33

A

0367-6234（2014）10-0037-05

2013-11-03.

国家自然科学基金资助项目（51178141）.

何忠华（1980—），男，博士研究生，讲师；袁一星（1957—），男，教授，博士生导师.

何忠华，hzh9913＠163.com.